Frequency domain
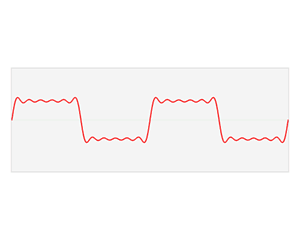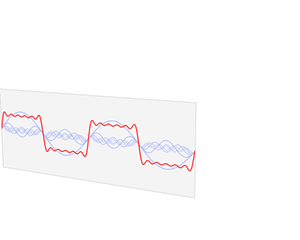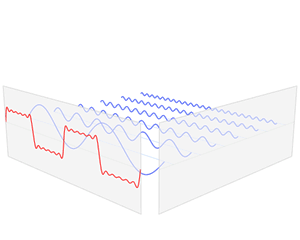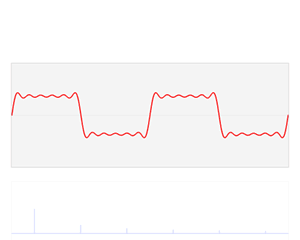
In mathematics, physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency (and possibly phase), rather than time, as in time series.[1] Put simply, a time-domain graph shows how a signal changes over time, whereas a frequency-domain graph shows how the signal is distributed within different frequency bands over a range of frequencies. A complex valued frequency-domain representation consists of both the magnitude and the phase of a set of sinusoids (or other basis waveforms) at the frequency components of the signal. Although it is common to refer to the magnitude portion (the real valued frequency-domain) as the frequency response of a signal, the phase portion is required to uniquely define the signal.
A given function or signal can be converted between the time and frequency domains with a pair of mathematical operators called transforms. An example is the Fourier transform, which converts a time function into a complex valued sum or integral of sine waves of different frequencies, with amplitudes and phases, each of which represents a frequency component. The "spectrum" of frequency components is the frequency-domain representation of the signal. The inverse Fourier transform converts the frequency-domain function back to the time-domain function. A spectrum analyzer is a tool commonly used to visualize electronic signals in the frequency domain.
A frequency-domain representation may describe either a static function or a particular time period of a dynamic function (signal or system). The frequency transform of a dynamic function is performed over a finite time period of that function and assumes the function repeats infinitely outside of that time period. Some specialized signal processing techniques for dynamic functions use transforms that result in a joint time–frequency domain, with the instantaneous frequency response being a key link between the time domain and the frequency domain.
Advantages
One of the main reasons for using a frequency-domain representation of a problem is to simplify the mathematical analysis. For mathematical systems governed by linear differential equations, a very important class of systems with many real-world applications, converting the description of the system from the time domain to a frequency domain converts the differential equations to algebraic equations, which are much easier to solve.
In addition, looking at a system from the point of view of frequency can often give an intuitive understanding of the qualitative behavior of the system, and a revealing scientific nomenclature has grown up to describe it, characterizing the behavior of physical systems to time varying inputs using terms such as bandwidth, frequency response, gain, phase shift, resonant frequencies, time constant, resonance width, damping factor, Q factor, harmonics, spectrum, power spectral density, eigenvalues, poles, and zeros.
An example of a field in which frequency-domain analysis gives a better understanding than time domain is music; the theory of operation of musical instruments and the musical notation used to record and discuss pieces of music is implicitly based on the breaking down of complex sounds into their separate component frequencies (musical notes).
Magnitude and phase
In using the Laplace, Z-, or Fourier transforms, a signal is described by a complex function of frequency: the component of the signal at any given frequency is given by a complex number. The modulus of the number is the amplitude of that component, and the argument is the relative phase of the wave. For example, using the Fourier transform, a sound wave, such as human speech, can be broken down into its component tones of different frequencies, each represented by a sine wave of a different amplitude and phase. The response of a system, as a function of frequency, can also be described by a complex function. In many applications, phase information is not important. By discarding the phase information, it is possible to simplify the information in a frequency-domain representation to generate a frequency spectrum or spectral density. A spectrum analyzer is a device that displays the spectrum, while the time-domain signal can be seen on an oscilloscope.
Types
Although "the" frequency domain is spoken of in the singular, there is a number of different mathematical transforms which are used to analyze time-domain functions and are referred to as "frequency domain" methods. These are the most common transforms, and the fields in which they are used:
- Fourier series – periodic signals, oscillating systems.
- Fourier transform – aperiodic signals, transients.
- Laplace transform – electronic circuits and control systems.
- Z transform – discrete-time signals, digital signal processing.
- Wavelet transform — image analysis, data compression.
More generally, one can speak of the transform domain with respect to any transform. The above transforms can be interpreted as capturing some form of frequency, and hence the transform domain is referred to as a frequency domain.
Discrete frequency domain
A discrete frequency domain is a frequency domain that is discrete rather than continuous. For example, the discrete Fourier transform maps a function having a discrete time domain into one having a discrete frequency domain. The discrete-time Fourier transform, on the other hand, maps functions with discrete time (discrete-time signals) to functions that have a continuous frequency domain.[2][3]
A periodic signal has energy only at a base frequency and its harmonics; thus it can be analyzed using a discrete frequency domain. A discrete-time signal gives rise to a periodic frequency spectrum. In a situation where both these conditions occur, a signal which is discrete and periodic results in a frequency spectrum which is also discrete and periodic; this is the usual context for a discrete Fourier transform.
History of term
The use of the terms "frequency domain" and "time domain" arose in communication engineering in the 1950s and early 1960s, with "frequency domain" appearing in 1953.[4] See time domain: origin of term for details.[5]
See also
- Bandwidth
- Blackman–Tukey transformation
- Fourier analysis for computing periodicity in evenly spaced data
- Least-squares spectral analysis for computing periodicity in unevenly spaced data
- Short-time Fourier transform
- Time–frequency representation
- Time–frequency analysis
- Wavelet
- Wavelet transform – digital image processing, signal compression
References
- ↑ Broughton, S. A.; Bryan, K. (2008). Discrete Fourier Analysis and Wavelets: Applications to Signal and Image Processing. New York: John Wiley & Sons. p. 72.
- ↑ C. Britton Rorabaugh (1998). DSP primer. McGraw-Hill Professional. p. 153. ISBN 978-0-07-054004-0. https://books.google.com/books?id=MYhMratb5gsC&pg=PA153.
- ↑ Shanbao Tong and Nitish Vyomesh Thakor (2009). Quantitative EEG analysis methods and clinical applications. Artech House. p. 53. ISBN 978-1-59693-204-3. https://books.google.com/books?id=joodLUTyIEYC&pg=PA53.
- ↑ Zadeh, L. A. (1953), "Theory of Filtering", Journal of the Society for Industrial and Applied Mathematics 1: 35–51, doi:10.1137/0101003
- ↑ Earliest Known Uses of Some of the Words of Mathematics (T), Jeff Miller, March 25, 2009
Goldshleger, N., Shamir, O., Basson, U., Zaady, E. (2019). Frequency Domain Electromagnetic Method (FDEM) as tool to study contamination at the sub-soil layer. Geoscience 9 (9), 382.
Further reading
- Boashash, B. (Sep 1988). "Note on the Use of the Wigner Distribution for Time Frequency Signal Analysis". IEEE Transactions on Acoustics, Speech, and Signal Processing 36 (9): 1518–1521. doi:10.1109/29.90380. http://espace.library.uq.edu.au/view/UQ:209682/Boashash_1988_WVD_analytic_signal.pdf..
- Boashash, B. (April 1992). "Estimating and Interpreting the Instantaneous Frequency of a Signal-Part I: Fundamentals". Proceedings of the IEEE 80 (4): 519–538. doi:10.1109/5.135376..
 |

