Physics:Electronic properties of graphene
This scientific article needs additional citations to secondary or tertiary sources (September 2017) (Learn how and when to remove this template message) |
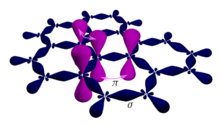
Graphene is a semimetal whose conduction and valence bands meet at the Dirac points, which are six locations in momentum space, the vertices of its hexagonal Brillouin zone, divided into two non-equivalent sets of three points. The two sets are labeled K and K'. The sets give graphene a valley degeneracy of gv = 2. By contrast, for traditional semiconductors the primary point of interest is generally Γ, where momentum is zero.[1] Four electronic properties separate it from other condensed matter systems.
Electronic spectrum
Electrons propagating through graphene's honeycomb lattice effectively lose their mass, producing quasi-particles that are described by a 2D analogue of the Dirac equation rather than the Schrödinger equation for spin-1⁄2 particles.[2][3]
Dispersion relation
When atoms are placed onto the graphene hexagonal lattice, the overlap between the pz(π) orbitals and the s or the px and py orbitals is zero by symmetry. The pz electrons forming the π bands in graphene can be treated independently. Within this π-band approximation, using a conventional tight-binding model, the dispersion relation (restricted to first-nearest-neighbor interactions only) that produces energy of the electrons with wave vector [math]\displaystyle{ \mathbf{k}=[k_x,k_y] }[/math] is[4][5]
- [math]\displaystyle{ E(\mathbf{k})=\pm\,\gamma_0\sqrt{1+4\cos^2{\tfrac{1}{2}a k_x}+4\cos{\tfrac{1}{2}a k_x} \cdot \cos{\tfrac{\sqrt{3}}{2}a k_y}} }[/math]
with the nearest-neighbor (π orbitals) hopping energy γ0 ≈ 2.8 eV and the lattice constant a ≈ 2.46 Å. The conduction and valence bands, respectively, correspond to the different signs. With one pz electron per atom in this model the valence band is fully occupied, while the conduction band is vacant. The two bands touch at the zone corners (the K point in the Brillouin zone), where there is a zero density of states but no band gap. The graphene sheet thus displays a semimetallic (or zero-gap semiconductor) character. Two of the six Dirac points are independent, while the rest are equivalent by symmetry. In the vicinity of the K-points the energy depends linearly on the wave vector, similar to a relativistic particle.[4][6] Since an elementary cell of the lattice has a basis of two atoms, the wave function has an effective 2-spinor structure.
As a consequence, at low energies, even neglecting the true spin, the electrons can be described by an equation that is formally equivalent to the massless Dirac equation. Hence, the electrons and holes are called Dirac fermions.[4] This pseudo-relativistic description is restricted to the chiral limit, i.e., to vanishing rest mass M0, which leads to additional features:[4][7]
- [math]\displaystyle{ - i v_F\, \vec \sigma \cdot \nabla \psi(\mathbf{r})\,=\,E\psi(\mathbf{r}). }[/math]
Here vF ~ 106 m/s (.003 c) is the Fermi velocity in graphene, which replaces the velocity of light in the Dirac theory; [math]\displaystyle{ \vec{\sigma} }[/math] is the vector of the Pauli matrices; [math]\displaystyle{ \psi(\mathbf{r}) }[/math] is the two-component wave function of the electrons and E is their energy.[2]
The equation describing the electrons' linear dispersion relation is
- [math]\displaystyle{ E(k)=\hbar v_F k }[/math]
where the wavevector [math]\displaystyle{ k=\sqrt{k_x^2+k_y^2} }[/math] is measured from the Dirac points (the zero of energy is chosen here to coincide with the Dirac points). The equation uses a pseudospin matrix formula that describes two sublattices of the honeycomb lattice.[6]
'Massive' electrons
Graphene's unit cell has two identical carbon atoms and two zero-energy states: one in which the electron resides on atom A, the other in which the electron resides on atom B. However, if the two atoms in the unit cell are not identical, the situation changes. Hunt et al. showed that placing hexagonal boron nitride (h-BN) in contact with graphene can alter the potential felt at atom A versus atom B enough that the electrons develop a mass and accompanying band gap of about 30 meV [0.03 Electron Volt (eV)].[8]
The mass can be positive or negative. An arrangement that slightly raises the energy of an electron on atom A relative to atom B gives it a positive mass, while an arrangement that raises the energy of atom B produces a negative electron mass. The two versions behave alike and are indistinguishable via optical spectroscopy. An electron traveling from a positive-mass region to a negative-mass region must cross an intermediate region where its mass once again becomes zero. This region is gapless and therefore metallic. Metallic modes bounding semiconducting regions of opposite-sign mass is a hallmark of a topological phase and display much the same physics as topological insulators.[8]
If the mass in graphene can be controlled, electrons can be confined to massless regions by surrounding them with massive regions, allowing the patterning of quantum dots, wires and other mesoscopic structures. It also produces one-dimensional conductors along the boundary. These wires would be protected against backscattering and could carry currents without dissipation.[8]
Single-atom wave propagation
Electron waves in graphene propagate within a single-atom layer, making them sensitive to the proximity of other materials such as high-κ dielectrics, superconductors and ferromagnetics.
Electron transport
Graphene displays remarkable electron mobility at room temperature, with reported values in excess of 15000 cm2⋅V−1⋅s−1.[9] Hole and electron mobilities were expected to be nearly identical.[3] The mobility is nearly independent of temperature between 10 K and 100 K,[10][11][12] which implies that the dominant scattering mechanism is defect scattering. Scattering by graphene's acoustic phonons intrinsically limits room temperature mobility to 200000 cm2⋅V−1⋅s−1 at a carrier density of 1012 cm−2,[12][13] 10×106 times greater than copper.[14]
The corresponding resistivity of graphene sheets would be 10−6 Ω⋅cm. This is less than the resistivity of silver, the lowest otherwise known at room temperature.[15] However, on SiO2 substrates, scattering of electrons by optical phonons of the substrate is a larger effect than scattering by graphene's own phonons. This limits mobility to 40000 cm2⋅V−1⋅s−1.[12]
Charge transport is affected by adsorption of contaminants such as water and oxygen molecules. This leads to non-repetitive and large hysteresis I-V characteristics. Researchers must carry out electrical measurements in vacuum. Graphene surfaces can be protected by a coating with materials such as SiN, PMMA and h-BN. In January 2015, the first stable graphene device operation in air over several weeks was reported, for graphene whose surface was protected by aluminum oxide.[16][17] In 2015 lithium-coated graphene was observed to exhibit superconductivity[18] and in 2017 evidence for unconventional superconductivity was demonstrated in single layer graphene placed on the electron-doped (non-chiral) d-wave superconductor Pr2−xCexCuO4 (PCCO).[19]
Electrical resistance in 40-nanometer-wide nanoribbons of epitaxial graphene changes in discrete steps. The ribbons' conductance exceeds predictions by a factor of 10. The ribbons can act more like optical waveguides or quantum dots, allowing electrons to flow smoothly along the ribbon edges. In copper, resistance increases in proportion to length as electrons encounter impurities.[20][21]
Transport is dominated by two modes. One is ballistic and temperature independent, while the other is thermally activated. Ballistic electrons resemble those in cylindrical carbon nanotubes. At room temperature, resistance increases abruptly at a particular length—the ballistic mode at 16 micrometres and the other at 160 nanometres.[20]
Graphene electrons can cover micrometer distances without scattering, even at room temperature.[2]
Despite zero carrier density near the Dirac points, graphene exhibits a minimum conductivity on the order of [math]\displaystyle{ 4e^2/h }[/math]. The origin of this minimum conductivity is unclear. However, rippling of the graphene sheet or ionized impurities in the SiO2 substrate may lead to local puddles of carriers that allow conduction.[3] Several theories suggest that the minimum conductivity should be [math]\displaystyle{ 4e^2/{(\pi}h) }[/math]; however, most measurements are of order [math]\displaystyle{ 4e^2/h }[/math] or greater[9] and depend on impurity concentration.[22]
Near zero carrier density graphene exhibits positive photoconductivity and negative photoconductivity at high carrier density. This is governed by the interplay between photoinduced changes of both the Drude weight and the carrier scattering rate.[23]
Graphene doped with various gaseous species (both acceptors and donors) can be returned to an undoped state by gentle heating in vacuum.[22][24] Even for dopant concentrations in excess of 1012 cm−2 carrier mobility exhibits no observable change.[24] Graphene doped with potassium in ultra-high vacuum at low temperature can reduce mobility 20-fold.[22][25] The mobility reduction is reversible on removing the potassium.
Due to graphene's two dimensions, charge fractionalization (where the apparent charge of individual pseudoparticles in low-dimensional systems is less than a single quantum[26]) is thought to occur. It may therefore be a suitable material for constructing quantum computers[27] using anyonic circuits.[28]
In 2018, superconductivity was reported in twisted bilayer graphene.
Excitonic properties
First-principle calculations with quasiparticle corrections and many-body effects explore the electronic and optical properties of graphene-based materials. The approach is described as three stages.[29] With GW calculation, the properties of graphene-based materials are accurately investigated, including bulk graphene,[30] nanoribbons,[31] edge and surface functionalized armchair oribbons,[32] hydrogen saturated armchair ribbons,[33] Josephson effect in graphene SNS junctions with single localized defect[34] and armchair ribbon scaling properties.[35]
Magnetic properties
In 2014 researchers magnetized graphene by placing it on an atomically smooth layer of magnetic yttrium iron garnet. The graphene's electronic properties were unaffected. Prior approaches involved doping.[36] The dopant's presence negatively affected its electronic properties.[37]
Strong magnetic fields
In magnetic fields of ≈10 tesla, additional plateaus of Hall conductivity at [math]\displaystyle{ \sigma_{xy}=\nu e^2/h }[/math] with [math]\displaystyle{ \nu=0,\pm {1},\pm {4} }[/math] are observed.[38] The observation of a plateau at [math]\displaystyle{ \nu=3 }[/math][39] and the fractional quantum Hall effect at [math]\displaystyle{ \nu=1/3 }[/math] were reported.[39][40]
These observations with [math]\displaystyle{ \nu=0,\pm 1,\pm 3, \pm 4 }[/math] indicate that the four-fold degeneracy (two valley and two spin degrees of freedom) of the Landau energy levels is partially or completely lifted.[41] One hypothesis is that the magnetic catalysis of symmetry breaking is responsible for lifting the degeneracy.[citation needed]
Spin transport
Graphene is claimed to be an ideal material for spintronics due to its small spin-orbit interaction and the near absence of nuclear magnetic moments in carbon (as well as a weak hyperfine interaction). Electrical spin current injection and detection has been demonstrated up to room temperature.[42][43][44] Spin coherence length above 1 micrometre at room temperature was observed,[42] and control of the spin current polarity with an electrical gate was observed at low temperature.[43]
Spintronic and magnetic properties can be present in graphene simultaneously.[45] Low-defect graphene nanomeshes manufactured using a non-lithographic method exhibit large-amplitude ferromagnetism even at room temperature. Additionally a spin pumping effect is found for fields applied in parallel with the planes of few-layer ferromagnetic nanomeshes, while a magnetoresistance hysteresis loop is observed under perpendicular fields.[citation needed]
Dirac fluid
Charged particles in high-purity graphene behave as a strongly interacting, quasi-relativistic plasma. The particles move in a fluid-like manner, traveling along a single path and interacting with high frequency. The behavior was observed in a graphene sheet faced on both sides with a h-BN crystal sheet.[46]
Anomalous quantum Hall effect
The quantum Hall effect is a quantum mechanical version of the Hall effect, which is the production of transverse (perpendicular to the main current) conductivity in the presence of a magnetic field. The quantization of the Hall effect [math]\displaystyle{ \sigma_{xy} }[/math] at integer multiples (the "Landau level") of the basic quantity [math]\displaystyle{ e^2/h }[/math] (where e is the elementary electric charge and h is Planck's constant) It can usually be observed only in very clean silicon or gallium arsenide solids at temperatures around 3 K and high magnetic fields.
Graphene shows the quantum Hall effect with respect to conductivity quantization: the effect is anomalous in that the sequence of steps is shifted by 1/2 with respect to the standard sequence and with an additional factor of 4. Graphene's Hall conductivity is [math]\displaystyle{ \sigma_{xy}=\pm {4\cdot\left(N + 1/2 \right)e^2}/h }[/math], where N is the Landau level and the double valley and double spin degeneracies give the factor of 4.[9] These anomalies are present at room temperature, i.e. at roughly 20 °C (293 K).[10]
This behavior is a direct result of graphene's massless Dirac electrons. In a magnetic field, their spectrum has a Landau level with energy precisely at the Dirac point. This level is a consequence of the Atiyah–Singer index theorem and is half-filled in neutral graphene,[4] leading to the "+1/2" in the Hall conductivity.[47] Bilayer graphene also shows the quantum Hall effect, but with only one of the two anomalies (i.e. [math]\displaystyle{ \sigma_{xy}=\pm {4\cdot N\cdot e^2}/h }[/math]). In the second anomaly, the first plateau at N=0 is absent, indicating that bilayer graphene stays metallic at the neutrality point.[9]
Unlike normal metals, graphene's longitudinal resistance shows maxima rather than minima for integral values of the Landau filling factor in measurements of the Shubnikov–de Haas oscillations, whereby the term integral quantum Hall effect. These oscillations show a phase shift of π, known as Berry's phase.[10][3] Berry's phase arises due to the zero effective carrier mass near the Dirac points.[48] The temperature dependence of the oscillations reveals that the carriers have a non-zero cyclotron mass, despite their zero effective mass.[10]
Graphene samples prepared on nickel films, and on both the silicon face and carbon face of silicon carbide, show the anomalous effect directly in electrical measurements.[49][50][51][52][53][54] Graphitic layers on the carbon face of silicon carbide show a clear Dirac spectrum in angle-resolved photoemission experiments. The effect is observed in cyclotron resonance and tunneling experiments.[55]
Casimir effect
The Casimir effect is an interaction between disjoint neutral bodies provoked by the fluctuations of the electrodynamical vacuum. Mathematically it can be explained by considering the normal modes of electromagnetic fields, which explicitly depend on the boundary (or matching) conditions on the interacting bodies' surfaces. Since graphene/electromagnetic field interaction is strong for a one-atom-thick material, the Casimir effect is of interest.[56][57]
Van der Waals force
The Van der Waals force (or dispersion force) is also unusual, obeying an inverse cubic, asymptotic power law in contrast to the usual inverse quartic.[58]
Effect of substrate
The electronic properties of graphene are significantly influenced by the supporting substrate.[59][60] The Si(100)/H surface does not perturb graphene's electronic properties, whereas the interaction between it and the clean Si(100) surface changes its electronic states significantly. This effect results from the covalent bonding between C and surface Si atoms, modifying the π-orbital network of the graphene layer. The local density of states shows that the bonded C and Si surface states are highly disturbed near the Fermi energy.
Comparison with nanoribbon
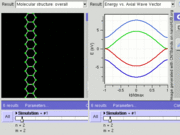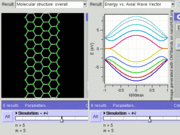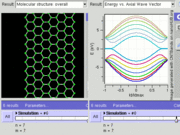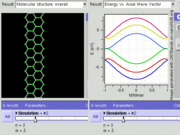
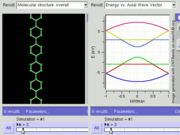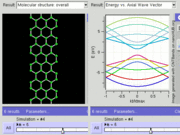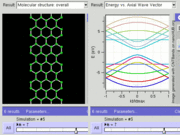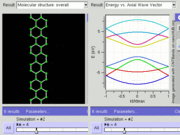
If the in-plane direction is confined, in which case it is referred to as a nanoribbon, its electronic structure is different. If it is "zig-zag" (diagram), the bandgap is zero. If it is "armchair" (diagram), the bandgap is non-zero (see figure).
GNR band structure for zig-zag orientation. Tightbinding calculations show that zig-zag orientation is always metallic.
GNR band structure for armchair orientation. Tightbinding calculations show that armchair orientation can be semiconducting or metallic depending on width (chirality).
References
- ↑ Cooper, Daniel R.; D’Anjou, Benjamin; Ghattamaneni, Nageswara; Harack, Benjamin; Hilke, Michael; Horth, Alexandre; Majlis, Norberto; Massicotte, Mathieu et al. (3 November 2011). "Experimental Review of Graphene". ISRN Condensed Matter Physics 2012: 1–56. doi:10.5402/2012/501686. http://michael-hilke.research.mcgill.ca/publications/cooper2012experimental.pdf. Retrieved 30 August 2016.
- ↑ 2.0 2.1 2.2 Neto, A Castro; Peres, N. M. R.; Novoselov, K. S.; Geim, A. K. (2009). "The electronic properties of graphene". Rev Mod Phys 81 (1): 109–162. doi:10.1103/RevModPhys.81.109. Bibcode: 2009RvMP...81..109C. http://onnes.ph.man.ac.uk/nano/Publications/RMP_2009.pdf.
- ↑ 3.0 3.1 3.2 3.3 Charlier, J.-C.; Eklund, P.C.; Zhu, J.; Ferrari, A.C. (2008). Jorio, A.; Dresselhaus and, G.; Dresselhaus, M.S.. eds. Electron and Phonon Properties of Graphene: Their Relationship with Carbon Nanotubes. Berlin/Heidelberg: Springer-Verlag. https://books.google.com/books?id=ammoVEI-H2gC.
- ↑ 4.0 4.1 4.2 4.3 4.4 Semenoff, G. W. (1984). "Condensed-Matter Simulation of a Three-Dimensional Anomaly". Physical Review Letters 53 (26): 2449–2452. doi:10.1103/PhysRevLett.53.2449. Bibcode: 1984PhRvL..53.2449S.
- ↑ Wallace, P.R. (1947). "The Band Theory of Graphite". Physical Review 71 (9): 622–634. doi:10.1103/PhysRev.71.622. Bibcode: 1947PhRv...71..622W.
- ↑ 6.0 6.1 Avouris, P.; Chen, Z.; Perebeinos, V. (2007). "Carbon-based electronics". Nature Nanotechnology 2 (10): 605–15. doi:10.1038/nnano.2007.300. PMID 18654384. Bibcode: 2007NatNa...2..605A.
- ↑ Lamas, C.A.; Cabra, D.C.; Grandi, N. (2009). "Generalized Pomeranchuk instabilities in graphene". Physical Review B 80 (7): 75108. doi:10.1103/PhysRevB.80.075108. Bibcode: 2009PhRvB..80g5108L.
- ↑ 8.0 8.1 8.2 Fuhrer, M. S. (2013). "Critical Mass in Graphene". Science 340 (6139): 1413–1414. doi:10.1126/science.1240317. PMID 23788788. Bibcode: 2013Sci...340.1413F.
- ↑ 9.0 9.1 9.2 9.3 Geim & Novoselov 2007.
- ↑ 10.0 10.1 10.2 10.3 Novoselov, K. S.; Geim, A. K.; Morozov, S. V.; Jiang, D.; Katsnelson, M. I.; Grigorieva, I. V.; Dubonos, S. V.; Firsov, A. A. (2005). "Two-dimensional gas of massless Dirac fermions in graphene". Nature 438 (7065): 197–200. doi:10.1038/nature04233. PMID 16281030. Bibcode: 2005Natur.438..197N.
- ↑ Morozov, S.V.; Novoselov, K.; Katsnelson, M.; Schedin, F.; Elias, D.; Jaszczak, J.; Geim, A. (2008). "Giant Intrinsic Carrier Mobilities in Graphene and Its Bilayer". Physical Review Letters 100 (1): 016602. doi:10.1103/PhysRevLett.100.016602. PMID 18232798. Bibcode: 2008PhRvL.100a6602M.
- ↑ 12.0 12.1 12.2 Chen, J. H.; Jang, Chaun; Xiao, Shudong; Ishigami, Masa; Fuhrer, Michael S. (2008). "Intrinsic and Extrinsic Performance Limits of Graphene Devices on SiO2". Nature Nanotechnology 3 (4): 206–9. doi:10.1038/nnano.2008.58. PMID 18654504.
- ↑ Akturk, A.; Goldsman, N. (2008). "Electron transport and full-band electron–phonon interactions in graphene". Journal of Applied Physics 103 (5): 053702–053702–8. doi:10.1063/1.2890147. Bibcode: 2008JAP...103e3702A.
- ↑ Kusmartsev, F. V.; Wu, W. M.; Pierpoint, M. P.; Yung, K. C. (2014). "Application of Graphene within Optoelectronic Devices and Transistors". arXiv:1406.0809 [cond-mat.mtrl-sci].
- ↑ Physicists Show Electrons Can Travel More Than 100 Times Faster in Graphene :: University Communications Newsdesk, University of Maryland . Newsdesk.umd.edu (24 March 2008). Retrieved on 2014-01-12.
- ↑ Sagade, A. A. (2015). "Highly Air Stable Passivation of Graphene Based Field Effect Devices". Nanoscale 7 (8): 3558–3564. doi:10.1039/c4nr07457b. PMID 25631337. Bibcode: 2015Nanos...7.3558S.
- ↑ "Graphene Devices Stand the Test of Time". 2015-01-22. https://spectrum.ieee.org/nanoclast/semiconductors/nanotechnology/graphene-devices-stand-the-test-of-time.
- ↑ "Researchers create superconducting graphene". 2015-09-09. http://www.rdmag.com/news/2015/09/researchers-create-superconducting-graphene.
- ↑ Di Bernardo, A.; Millo, O.; Barbone, M.; Alpern, H.; Kalcheim, Y.; Sassi, U.; Ott, A. K.; Fazio, D. De et al. (2017-01-19). "p-wave triggered superconductivity in single-layer graphene on an electron-doped oxide superconductor" (in en). Nature Communications 8: 14024. doi:10.1038/ncomms14024. ISSN 2041-1723. PMID 28102222. Bibcode: 2017NatCo...814024D.
- ↑ 20.0 20.1 "New form of graphene allows electrons to behave like photons". kurzweilai.net. http://www.kurzweilai.net/new-form-of-graphene-allows-electrons-to-behave-like-photons.
- ↑ Baringhaus, J.; Ruan, M.; Edler, F.; Tejeda, A.; Sicot, M.; Taleb-Ibrahimi, A.; Li, A. P.; Jiang, Z. et al. (2014). "Exceptional ballistic transport in epitaxial graphene nanoribbons". Nature 506 (7488): 349–354. doi:10.1038/nature12952. PMID 24499819. Bibcode: 2014Natur.506..349B.
- ↑ 22.0 22.1 22.2 Chen, J. H.; Jang, C.; Adam, S.; Fuhrer, M. S.; Williams, E. D.; Ishigami, M. (2008). "Charged Impurity Scattering in Graphene". Nature Physics 4 (5): 377–381. doi:10.1038/nphys935. Bibcode: 2008NatPh...4..377C.
- ↑ Light pulses control how graphene conducts electricity. kurzweilai.net. 4 August 2014
- ↑ 24.0 24.1 Schedin, F.; Geim, A. K.; Morozov, S. V.; Hill, E. W.; Blake, P.; Katsnelson, M. I.; Novoselov, K. S. (2007). "Detection of individual gas molecules adsorbed on graphene". Nature Materials 6 (9): 652–655. doi:10.1038/nmat1967. PMID 17660825. Bibcode: 2007NatMa...6..652S.
- ↑ Adam, S.; Hwang, E. H.; Galitski, V. M.; Das Sarma, S. (2007). "A self-consistent theory for graphene transport". Proc. Natl. Acad. Sci. USA 104 (47): 18392–7. doi:10.1073/pnas.0704772104. PMID 18003926. Bibcode: 2007PNAS..10418392A.
- ↑ Steinberg, Hadar et al. (2008). "Charge fractionalization in quantum wires". Nature Physics 4 (2): 116–119. doi:10.1038/nphys810. Bibcode: 2008NatPh...4..116S.
- ↑ Trisetyarso, Agung (2012). "Dirac four-potential tunings-based quantum transistor utilizing the Lorentz force". Quantum Information & Computation 12 (11–12): 989. doi:10.26421/QIC12.11-12-7. Bibcode: 2010arXiv1003.4590T. http://dl.acm.org/citation.cfm?id=2481569.2481576.
- ↑ Pachos, Jiannis K. (2009). "Manifestations of topological effects in graphene". Contemporary Physics 50 (2): 375–389. doi:10.1080/00107510802650507. Bibcode: 2009ConPh..50..375P.
Franz, M. (5 January 2008). "Fractionalization of charge and statistics in graphene and related structures". University of British Columbia. http://www.int.washington.edu/talks/WorkShops/int_08_37W/People/Franz_M/Franz.pdf. - ↑ Onida, Giovanni; Rubio, Angel (2002). "Electronic excitations: Density-functional versus many-body Green's-function approaches". Rev. Mod. Phys. 74 (2): 601–659. doi:10.1103/RevModPhys.74.601. Bibcode: 2002RvMP...74..601O. https://digital.csic.es/bitstream/10261/98472/1/Electronic%20excitations.pdf.
- ↑ Yang, Li; Deslippe, Jack; Park, Cheol-Hwan; Cohen, Marvin; Louie, Steven (2009). "Excitonic Effects on the Optical Response of Graphene and Bilayer Graphene". Physical Review Letters 103 (18): 186802. doi:10.1103/PhysRevLett.103.186802. PMID 19905823. Bibcode: 2009PhRvL.103r6802Y.
- ↑ Prezzi, Deborah; Varsano, Daniele; Ruini, Alice; Marini, Andrea; Molinari, Elisa (2008). "Optical properties of graphene nanoribbons: The role of many-body effects". Physical Review B 77 (4): 041404. doi:10.1103/PhysRevB.77.041404. Bibcode: 2008PhRvB..77d1404P.Yang, Li; Cohen, Marvin L.; Louie, Steven G. (2007). "Excitonic Effects in the Optical Spectra of Graphene Nanoribbons". Nano Letters 7 (10): 3112–5. doi:10.1021/nl0716404. PMID 17824720. Bibcode: 2007NanoL...7.3112Y.Yang, Li; Cohen, Marvin L.; Louie, Steven G. (2008). "Magnetic Edge-State Excitons in Zigzag Graphene Nanoribbons". Physical Review Letters 101 (18): 186401. doi:10.1103/PhysRevLett.101.186401. PMID 18999843. Bibcode: 2008PhRvL.101r6401Y.
- ↑ Zhu, Xi; Su, Haibin (2010). "Excitons of Edge and Surface Functionalized Graphene Nanoribbons". J. Phys. Chem. C 114 (41): 17257–17262. doi:10.1021/jp102341b.
- ↑ Wang, Min; Li, Chang Ming (2011). "Excitonic properties of hydrogen saturation-edged armchair graphene nanoribbons". Nanoscale 3 (5): 2324–8. doi:10.1039/c1nr10095e. PMID 21503364. Bibcode: 2011Nanos...3.2324W.
- ↑ Bolmatov, Dima; Mou, Chung-Yu (2010). "Josephson effect in graphene SNS junction with a single localized defect". Physica B 405 (13): 2896–2899. doi:10.1016/j.physb.2010.04.015. Bibcode: 2010PhyB..405.2896B.Bolmatov, Dima; Mou, Chung-Yu (2010). "Tunneling conductance of the graphene SNS junction with a single localized defect". Journal of Experimental and Theoretical Physics 110 (4): 613–617. doi:10.1134/S1063776110040084. Bibcode: 2010JETP..110..613B.
- ↑ Zhu, Xi; Su, Haibin (2011). "Scaling of Excitons in Graphene Nanoribbons with Armchair Shaped Edges". Journal of Physical Chemistry A 115 (43): 11998–12003. doi:10.1021/jp202787h. PMID 21939213. Bibcode: 2011JPCA..11511998Z.
- ↑ T. Hashimoto, S. Kamikawa, Y. Yagi, J. Haruyama, H. Yang, M. Chshiev, "Graphene edge spins: spintronics and magnetism in graphene nanomeshes", February 2014, Volume 5, Issue 1, pp 25
- ↑ Coxworth, Ben (27 January 2015). "Scientists give graphene one more quality – magnetism". Gizmag. http://www.gizmag.com/magnetized-graphene/35805.
- ↑ Zhang, Y.; Jiang, Z.; Small, J. P.; Purewal, M. S.; Tan, Y.-W.; Fazlollahi, M.; Chudow, J. D.; Jaszczak, J. A. et al. (2006). "Landau-Level Splitting in Graphene in High Magnetic Fields". Physical Review Letters 96 (13): 136806. doi:10.1103/PhysRevLett.96.136806. PMID 16712020. Bibcode: 2006PhRvL..96m6806Z.
- ↑ 39.0 39.1 Du, X.; Skachko, Ivan; Duerr, Fabian; Luican, Adina; Andrei, Eva Y. (2009). "Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene". Nature 462 (7270): 192–195. doi:10.1038/nature08522. PMID 19829294. Bibcode: 2009Natur.462..192D.
- ↑ Bolotin, K.; Ghahari, Fereshte; Shulman, Michael D.; Stormer, Horst L.; Kim, Philip (2009). "Observation of the fractional quantum Hall effect in graphene". Nature 462 (7270): 196–199. doi:10.1038/nature08582. PMID 19881489. Bibcode: 2009Natur.462..196B.
- ↑ Abergel, D.S.L.; Apalkov, V.; Berashevich, J.; Ziegler, K.; Chakraborty, Tapash (July 2010). "Properties of graphene: a theoretical perspective" (in en). Advances in Physics 59 (4): 261–482. doi:10.1080/00018732.2010.487978. ISSN 0001-8732. Bibcode: 2010AdPhy..59..261A. https://www.tandfonline.com/doi/full/10.1080/00018732.2010.487978.
- ↑ 42.0 42.1 Tombros, Nikolaos (2007). "Electronic spin transport and spin precession in single graphene layers at room temperature". Nature 448 (7153): 571–575. doi:10.1038/nature06037. PMID 17632544. Bibcode: 2007Natur.448..571T.
- ↑ 43.0 43.1 Cho, Sungjae; Chen, Yung-Fu; Fuhrer, Michael S. (2007). "Gate-tunable Graphene Spin Valve". Applied Physics Letters 91 (12): 123105. doi:10.1063/1.2784934. Bibcode: 2007ApPhL..91l3105C.
- ↑ Ohishi, Megumi (2007). "Spin Injection into a Graphene Thin Film at Room Temperature". Jpn J Appl Phys 46 (25): L605–L607. doi:10.1143/JJAP.46.L605. Bibcode: 2007JaJAP..46L.605O.
- ↑ Hashimoto, T.; Kamikawa, S.; Yagi, Y.; Haruyama, J.; Yang, H.; Chshiev, M. (2014). "Graphene edge spins: spintronics and magnetism in graphene nanomeshes". Nanosystems: Physics, Chemistry, Mathematics 5 (1): 25–38. http://nanojournal.ifmo.ru/en/wp-content/uploads/2014/02/NPCM51_P25-38.pdf.
- ↑ Borghino, Dario (February 15, 2016). "Liquid-like graphene could be the key to understanding black holes". New Atlas. http://newatlas.com/liquid-graphene-dirac-fluid/41801.
- ↑ Gusynin, V. P.; Sharapov, S. G. (2005). "Unconventional Integer Quantum Hall Effect in Graphene". Physical Review Letters 95 (14): 146801. doi:10.1103/PhysRevLett.95.146801. PMID 16241680. Bibcode: 2005PhRvL..95n6801G.
- ↑ Zhang, Y.; Tan, Y. W.; Stormer, H. L.; Kim, P. (2005). "Experimental observation of the quantum Hall effect and Berry's phase in graphene". Nature 438 (7065): 201–204. doi:10.1038/nature04235. PMID 16281031. Bibcode: 2005Natur.438..201Z.
- ↑ Kim, Kuen Soo; Zhao, Yue; Jang, Houk; Lee, Sang Yoon; Kim, Jong Min; Kim, Kwang S.; Ahn, Jong-Hyun; Kim, Philip et al. (2009). "Large-scale pattern growth of graphene films for stretchable transparent electrodes". Nature 457 (7230): 706–10. doi:10.1038/nature07719. PMID 19145232. Bibcode: 2009Natur.457..706K.
- ↑ Jobst, Johannes; Waldmann, Daniel; Speck, Florian; Hirner, Roland; Maude, Duncan K.; Seyller, Thomas; Weber, Heiko B. (2009). "How Graphene-like is Epitaxial Graphene? Quantum Oscillations and Quantum Hall Effect". Physical Review B 81 (19): 195434. doi:10.1103/PhysRevB.81.195434. Bibcode: 2010PhRvB..81s5434J.
- ↑ Shen, T.; Gu, J.J.; Xu, M; Wu, Y.Q.; Bolen, M.L.; Capano, M.A.; Engel, L.W.; Ye, P.D. (2009). "Observation of quantum-Hall effect in gated epitaxial graphene grown on SiC (0001)". Applied Physics Letters 95 (17): 172105. doi:10.1063/1.3254329. Bibcode: 2009ApPhL..95q2105S.
- ↑ Wu, Xiaosong; Hu, Yike; Ruan, Ming; Madiomanana, Nerasoa K; Hankinson, John; Sprinkle, Mike; Berger, Claire; de Heer, Walt A. (2009). "Half integer quantum Hall effect in high mobility single layer epitaxial graphene". Applied Physics Letters 95 (22): 223108. doi:10.1063/1.3266524. Bibcode: 2009ApPhL..95v3108W.
- ↑ Lara-Avila, Samuel; Kalaboukhov, Alexei; Paolillo, Sara; Syväjärvi, Mikael; Yakimova, Rositza; Fal'ko, Vladimir; Tzalenchuk, Alexander; Kubatkin, Sergey (7 July 2009). "SiC Graphene Suitable For Quantum Hall Resistance Metrology". Science Brevia. Bibcode: 2009arXiv0909.1193L.
- ↑ Alexander-Webber, J.A.; Baker, A.M.R.; Janssen, T.J.B.M.; Tzalenchuk, A.; Lara-Avila, S.; Kubatkin, S.; Yakimova, R.; Piot, B. A. et al. (2013). "Phase Space for the Breakdown of the Quantum Hall Effect in Epitaxial Graphene". Physical Review Letters 111 (9): 096601. doi:10.1103/PhysRevLett.111.096601. PMID 24033057. Bibcode: 2013PhRvL.111i6601A.
- ↑ Fuhrer, Michael S. (2009). "A physicist peels back the layers of excitement about graphene". Nature 459 (7250): 1037. doi:10.1038/4591037e. PMID 19553953. Bibcode: 2009Natur.459.1037F.
- ↑ Bordag, M.; Fialkovsky, I. V.; Gitman, D. M.; Vassilevich, D. V. (2009). "Casimir interaction between a perfect conductor and graphene described by the Dirac model". Physical Review B 80 (24): 245406. doi:10.1103/PhysRevB.80.245406. Bibcode: 2009PhRvB..80x5406B.
- ↑ Fialkovsky, I. V.; Marachevsky, V.N.; Vassilevich, D. V. (2011). "Finite temperature Casimir effect for graphene". Physical Review B 84 (35446): 35446. doi:10.1103/PhysRevB.84.035446. Bibcode: 2011PhRvB..84c5446F.
- ↑ Dobson, J. F.; White, A.; Rubio, A. (2006). "Asymptotics of the dispersion interaction: analytic benchmarks for van der Waals energy functionals". Physical Review Letters 96 (7): 073201. doi:10.1103/PhysRevLett.96.073201. PMID 16606085. Bibcode: 2006PhRvL..96g3201D.
- ↑ Xu, Yang; He, K. T.; Schmucker, S. W.; Guo, Z.; Koepke, J. C.; Wood, J. D.; Lyding, J. W.; Aluru, N. R. (2011). "Inducing Electronic Changes in Graphene through Silicon (100) Substrate Modification". Nano Letters 11 (7): 2735–2742. doi:10.1021/nl201022t. PMID 21661740. Bibcode: 2011NanoL..11.2735X.
- ↑ Pantano, Maria F. (July 2019). "Investigation of charges-driven interaction between graphene and different SiO2 surfaces". Carbon 148: 336–343. doi:10.1016/j.carbon.2019.03.071. https://qmro.qmul.ac.uk/xmlui/handle/123456789/57704.
Works cited
- Geim, A. K.; Novoselov, K. S. (2007). "The rise of graphene". Nature Materials 6 (3): 183–191. doi:10.1038/nmat1849. PMID 17330084. Bibcode: 2007NatMa...6..183G.
External links
 |