Kelvin
| kelvin | |
|---|---|
 Equivalent temperatures in kelvin (K), Celsius (°C), and Fahrenheit (°F) | |
| General information | |
| Unit system | SI |
| Unit of | temperature |
| Symbol | K |
| Named after | William Thomson, 1st Baron Kelvin |
| 2019 definition | kB ≝ 1.380649×10−23 J/K |
| Conversions | |
| Template:Calculator K in ... | ... corresponds to ... |
| Celsius scale | Template:Calculator °C |
| Fahrenheit scale | Template:Calculator °F |
| Rankine scale | Template:Calculator °Ra |
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K.[1][2][3][4] By definition, the Celsius scale (symbol °C) and the Kelvin scale have the exact same magnitude; that is, a rise of 1 K is equal to a rise of 1 °C and vice versa, and any temperature in degrees Celsius can be converted to kelvin by adding 273.15.[1][5]
The 19th century British scientist Lord Kelvin first developed and proposed the scale.[5] It was often called the "absolute Celsius" scale in the early 20th century.[6] The kelvin was formally added to the International System of Units in 1954, defining 273.16 K to be the triple point of water. The Celsius, Fahrenheit, and Rankine scales were redefined in terms of the Kelvin scale using this definition.[2][7][8] The 2019 revision of the SI now defines the kelvin in terms of energy by setting the Boltzmann constant; every 1 K change of thermodynamic temperature corresponds to a change in the thermal energy, kBT, of exactly 1.380649×10−23 J⋅K−1.[2]
History
Precursors

During the 18th century, multiple temperature scales were developed,[9] notably Fahrenheit and centigrade (later Celsius). These scales predated much of the modern science of thermodynamics, including atomic theory and the kinetic theory of gases which underpin the concept of absolute zero. Instead, they chose defining points within the range of human experience that could be reproduced easily and with reasonable accuracy, but lacked any deep significance in thermal physics. In the case of the Celsius scale (and the long defunct Newton and Réaumur scales) the melting point of ice served as such a starting point, with Celsius being defined (from the 1740s to the 1940s) by calibrating a thermometer such that:
- Water's freezing point is 0 °C.
- Water's boiling point is 100 °C.
This definition assumes pure water at a specific pressure chosen to approximate the natural air pressure at sea level. Thus, an increment of 1 °C equals 1/100 of the temperature difference between the melting and boiling points. The same temperature interval was later used for the Kelvin scale.
Charles's law
From 1787 to 1802, it was determined by Jacques Charles (unpublished), John Dalton,[10][11] and Joseph Louis Gay-Lussac[12] that, at constant pressure, ideal gases expanded or contracted their volume linearly (Charles's law) by about 1/273 parts per degree Celsius of temperature's change up or down, between 0 °C and 100 °C. Extrapolation of this law suggested that a gas cooled to about −273 °C would occupy zero volume.
Lord Kelvin

First absolute scale
In 1848, William Thomson, who was later ennobled as Lord Kelvin, published a paper On an Absolute Thermometric Scale.[13] The scale proposed in the paper turned out to be unsatisfactory, but the principles and formulas upon which the scale was based were correct.[14] For example, in a footnote, Thomson derived the value of −273 °C for absolute zero by calculating the negative reciprocal of 0.00366—the coefficient of thermal expansion of an ideal gas per degree Celsius relative to the ice point.[15] This derived value agrees with the currently accepted value of −273.15 °C, allowing for the precision and uncertainty involved in the calculation.
The scale was designed on the principle that "a unit of heat descending from a body A at the temperature T° of this scale, to a body B at the temperature (T − 1)°, would give out the same mechanical effect, whatever be the number T."[16] Specifically, Thomson expressed the amount of work necessary to produce a unit of heat (the thermal efficiency) as , where is the temperature in Celsius, is the coefficient of thermal expansion, and was "Carnot's function", a substance-independent quantity depending on temperature,[17] motivated by an obsolete version of Carnot's theorem.[14][18] The scale is derived by finding a change of variables of temperature such that is proportional to .

When Thomson published his paper in 1848, he only considered Regnault's experimental measurements of .[19] That same year, James Prescott Joule suggested to Thomson that the true formula for Carnot's function was[20] where is "the mechanical equivalent of a unit of heat",[21] now referred to as the specific heat capacity of water, approximately 771.8 foot-pounds force per degree Fahrenheit per pound (4,153 J/K/kg).[22] Thomson was initially skeptical of the deviations of Joule's formula from experiment, stating "I think it will be generally admitted that there can be no such inaccuracy in Regnault's part of the data, and there remains only the uncertainty regarding the density of saturated steam".[23] Thomson referred to the correctness of Joule's formula as "Mayer's hypothesis", on account of it having been first assumed by Mayer.[24] Thomson arranged numerous experiments in coordination with Joule, eventually concluding by 1854 that Joule's formula was correct and the effect of temperature on the density of saturated steam accounted for all discrepancies with Regnault's data.[25] Therefore, in terms of the modern Kelvin scale , the first scale could be expressed as follows:[18] The parameters of the scale were arbitrarily chosen to coincide with the Celsius scale at 0° and 100 °C or 273 and 373 K (the melting and boiling points of water).[26] On this scale, an increase of approximately 222 degrees corresponds to a doubling of Kelvin temperature, regardless of the starting temperature, and "infinite cold" (absolute zero) has a numerical value of negative infinity.[27]
Modern absolute scale
Thomson understood that with Joule's proposed formula for , the relationship between work and heat for a perfect thermodynamic engine was simply the constant .[28] In 1854, Thomson and Joule thus formulated a second absolute scale that was more practical and convenient, agreeing with air thermometers for most purposes.[29] Specifically, "the numerical measure of temperature shall be simply the mechanical equivalent of the thermal unit divided by Carnot's function."[30]
To explain this definition, consider a reversible Carnot cycle engine, where is the amount of heat energy transferred into the system, is the heat leaving the system, is the work done by the system (), is the temperature of the hot reservoir in degrees Celsius, and is the temperature of the cold reservoir in Celsius. The Carnot function is defined as , and the absolute temperature as . One finds the relationship . By supposing , one obtains the general principle of an absolute thermodynamic temperature scale for the Carnot engine, . The definition can be shown to correspond to the thermometric temperature of the ideal gas laws.[31]
This definition by itself is not sufficient. Thomson specified that the scale should have two properties:[32]
- The absolute values of two temperatures are to one another in the proportion of the heat taken in to the heat rejected in a perfect thermodynamic engine working with a source and refrigerator at the higher and lower of the temperatures respectively.
- The difference of temperatures between the freezing- and boiling-points of water under standard atmospheric pressure shall be called 100 degrees. (The same increment as the Celsius scale) Thomson's best estimates at the time were that the temperature of freezing water was 273.7 K and the temperature of boiling water was 373.7 K.[33]
These two properties would be featured in all future versions of the Kelvin scale, although it was not yet known by that name. In the early decades of the 20th century, the Kelvin scale was often called the "absolute Celsius" scale, indicating Celsius degrees counted from absolute zero rather than the freezing point of water, and using the same symbol for regular Celsius degrees, °C.[6]
Triple point standard
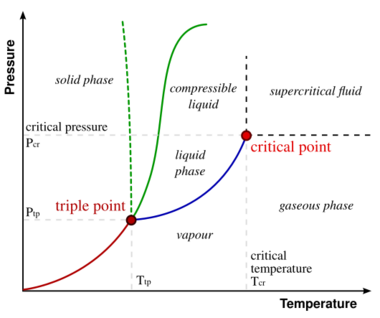
In 1873, William Thomson's older brother James coined the term triple point[34] to describe the combination of temperature and pressure at which the solid, liquid, and gas phases of a substance were capable of coexisting in thermodynamic equilibrium. While any two phases could coexist along a range of temperature-pressure combinations (e.g. the boiling point of water can be affected quite dramatically by raising or lowering the pressure), the triple point condition for a given substance can occur only at a single pressure and only at a single temperature. By the 1940s, the triple point of water had been experimentally measured to be about 0.6% of standard atmospheric pressure and very close to 0.01 °C per the historical definition of Celsius then in use.
In 1948, the Celsius scale was recalibrated by assigning the triple point temperature of water the value of 0.01 °C exactly[35] and allowing the melting point at standard atmospheric pressure to have an empirically determined value (and the actual melting point at ambient pressure to have a fluctuating value) close to 0 °C. This was justified on the grounds that the triple point was judged to give a more accurately reproducible reference temperature than the melting point.[36] The triple point could be measured with ±0.0001 °C accuracy, while the melting point just to ±0.001 °C.[35]
In 1954, with absolute zero having been experimentally determined to be about −273.15 °C per the definition of °C then in use, Resolution 3 of the 10th General Conference on Weights and Measures (CGPM) introduced a new internationally standardized Kelvin scale which defined the triple point as exactly 273.15 + 0.01 = 273.16 degrees Kelvin.[37][38]
In 1967/1968, Resolution 3 of the 13th CGPM renamed the unit increment of thermodynamic temperature "kelvin", symbol K, replacing "degree Kelvin", symbol .[39][40][41] The 13th CGPM also held in Resolution 4 that "The kelvin, unit of thermodynamic temperature, is equal to the fraction 1/273.16 of the thermodynamic temperature of the triple point of water."[4][42][43]
After the 1983 redefinition of the metre, this left the kelvin, the second, and the kilogram as the only SI units not defined with reference to any other unit.
In 2005, noting that the triple point could be influenced by the isotopic ratio of the hydrogen and oxygen making up a water sample and that this was "now one of the major sources of the observed variability between different realizations of the water triple point", the International Committee for Weights and Measures (CIPM), a committee of the CGPM, affirmed that for the purposes of delineating the temperature of the triple point of water, the definition of the kelvin would refer to water having the isotopic composition specified for Vienna Standard Mean Ocean Water.[4][44][45]
2019 redefinition

The Boltzmann constant kB serves as the bridge in the relation E = kBT, linking characteristic microscopic energies to the macroscopic temperature scale.[46] In the International System of Units (SI), the kelvin has traditionally been treated as an independent base unit with its own dimension. By contrast, in fundamental physics it is common to adopt natural units by setting the Boltzmann constant equal to unity, so that temperature and energy share the same units.[46][47]
In 2005, the CIPM began a programme to redefine the kelvin in terms of the Boltzmann constant, alongside exploring new definitions for several other SI base units in terms of fundamental constants. The motivation was to allow more accurate measurements at temperatures far away from the triple point of water, and to be independent from any particular substance or measurement.[48] Originally slated for adoption in 2011 with the Boltzmann constant being 1.38065X×10−23 J/K, X to be determined,[49] concerns arose about maintaining the precision of the triple point, and the redefinition was postponed until such time as more accurate measurements could be made, with these experiments taking several years in some cases.[50][51] Ultimately, the kelvin redefinition became part of the larger 2019 revision of the SI. In late 2018, the 26th General Conference on Weights and Measures (CGPM) adopted the value of kB = 1.380649×10−23 J⋅K−1[52][49][1][2][4][53] and the new definition officially came into force on 20 May 2019, the 144th anniversary of the Metre Convention.[53][1][2][4]
With this new definition, the kelvin now only depends on the Boltzmann constant and universal constants (see 2019 SI unit dependencies diagram), allowing the kelvin to be expressed as:[2]
In practical terms, as was the goal,[48] the change went largely unnoticed: the chosen value has enough accuracy and significant figures for continuity, ensuring that water still freezes at 0 °C to high precision.[54] The difference lies in the status of reference points. Before the redefinition, the triple point of water was taken as exact, while the Boltzmann constant had a measured value of 1.38064903(51)×10−23 J/K, with a relative standard uncertainty of 3.7×10−7.[55] Afterward, the Boltzmann constant was exact and the uncertainty is transferred to the triple point of water, which is now 273.1600(1) K.[lower-alpha 1]
On a deeper level, the kelvin is now defined in terms of the joule, making the separate existence of a temperature dimension theoretically unnecessary. The kelvin could have been redefined as a non-coherent derived SI unit, with 1 K = 1.380649×10−23 J.[46][57] Yet, "for historical and especially practical reasons, the kelvin will continue to be a base unit of the SI".[58]
Practical uses

Colour temperature
The kelvin is often used as a measure of the colour temperature of light sources. Colour temperature is based upon the principle that a black body radiator emits light with a frequency distribution characteristic of its temperature. Black bodies at temperatures below about 4000 K appear reddish, whereas those above about 7500 K appear bluish. Colour temperature is important in the fields of image projection and photography, where a colour temperature of approximately 5600 K is required to match "daylight" film emulsions.
In astronomy, the stellar classification of stars and their place on the Hertzsprung–Russell diagram are based, in part, upon their surface temperature, known as effective temperature. The photosphere of the Sun, for instance, has an effective temperature of 5772 K[59][60][61][62] as adopted by IAU 2015 Resolution B3.
Digital cameras and photographic software often use colour temperature in K in edit and setup menus. The simple guide is that higher colour temperature produces an image with enhanced white and blue hues. The reduction in colour temperature produces an image more dominated by reddish, "warmer" colours.
Kelvin as a unit of noise temperature
For electronics, the kelvin is used as an indicator of how noisy a circuit is in relation to an ultimate noise floor, i.e. the noise temperature. The Johnson–Nyquist noise of resistors (which produces an associated kTC noise when combined with capacitors) is a type of thermal noise derived from the Boltzmann constant and can be used to determine the noise temperature of a circuit using the Friis formulas for noise.
Derived units and SI multiples
The only SI derived unit with a special name derived from the kelvin is the degree Celsius. Like other SI units, the kelvin can also be modified by adding a metric prefix that multiplies it by a power of 10:
| Submultiples | Multiples | |||||
|---|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name | |
| 10−1 K | dK | decikelvin | 101 K | daK | decakelvin | |
| 10−2 K | cK | centikelvin | 102 K | hK | hectokelvin | |
| 10−3 K | mK | millikelvin | 103 K | kK | kilokelvin | |
| 10−6 K | µK | microkelvin | 106 K | MK | megakelvin | |
| 10−9 K | nK | nanokelvin | 109 K | GK | gigakelvin | |
| 10−12 K | pK | picokelvin | 1012 K | TK | terakelvin | |
| 10−15 K | fK | femtokelvin | 1015 K | PK | petakelvin | |
| 10−18 K | aK | attokelvin | 1018 K | EK | exakelvin | |
| 10−21 K | zK | zeptokelvin | 1021 K | ZK | zettakelvin | |
| 10−24 K | yK | yoctokelvin | 1024 K | YK | yottakelvin | |
Orthography
According to SI convention, the kelvin is never referred to nor written as a degree. The word "kelvin" is not capitalized when used as a unit. It may be in plural form as appropriate (for example, "it is 283 kelvins outside", as for "it is 50 degrees Fahrenheit" and "10 degrees Celsius").[5][63][64][65] The unit's symbol K is a capital letter,[39] per the SI convention to capitalize symbols of units derived from the name of a person.[66] It is common convention to capitalize Kelvin when referring to Lord Kelvin[5] or the Kelvin scale.[67]
The unit symbol K is encoded in Unicode at code point U+212A K KELVIN SIGN. However, this is a compatibility character provided for compatibility with legacy encodings. The Unicode standard recommends using U+004B K LATIN CAPITAL LETTER K instead; that is, a normal capital K. "Three letterlike symbols have been given canonical equivalence to regular letters: U+2126 Ω OHM SIGN, U+212A K KELVIN SIGN, and U+212B Å ANGSTROM SIGN. In all three instances, the regular letter should be used."[68]
See also
- Comparison of temperature scales
- International Temperature Scale of 1990
- kT (energy) – product of the Boltzmann constant and temperature
- Negative temperature
- Outline of metrology and measurement
Obsolete temperature scales include:
Notes
References
- ↑ 1.0 1.1 1.2 1.3 BIPM (20 May 2019). "Mise en pratique for the definition of the kelvin in the SI". https://www.bipm.org/documents/20126/41489682/SI-App2-kelvin.pdf/cd36cb68-3f00-05fd-339e-452df0b6215e?version=1.5&t=1637237805352&download=false.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 "SI Brochure: The International System of Units (SI) – 9th edition (updated in 2022)". BIPM. https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf/2d2b50bf-f2b4-9661-f402-5f9d66e4b507.
- ↑ "SI base unit: kelvin (K)". BIPM. https://www.bipm.org/en/si-base-units/kelvin.
- ↑ 4.0 4.1 4.2 4.3 4.4 "A Turning Point for Humanity: Redefining the World's Measurement System". NIST. 12 May 2018. https://www.nist.gov/si-redefinition/turning-point-humanity-redefining-worlds-measurement-system. Retrieved 21 February 2022.
- ↑ 5.0 5.1 5.2 5.3 "Kelvin: Introduction" (in en). 14 May 2018. https://www.nist.gov/si-redefinition/kelvin-introduction.
- ↑ 6.0 6.1 Encyclopaedia Britannica editions from the 1920s and 1950s, the article "Planets".
- ↑ "Busting Myths about the Metric System". NIST (Taking Measure (official blog of the NIST)). 6 October 2020. https://www.nist.gov/blogs/taking-measure/busting-myths-about-metric-system. Retrieved 21 February 2022.
- ↑ "Handbook 44 – 2022 – Appendix C – General Tables of Units of Measurement". NIST. https://www.nist.gov/system/files/documents/2021/11/30/2022-HB44-Section-Appendix-C.pdf.
- ↑ "Kelvin: History". NIST. 14 May 2018. https://www.nist.gov/si-redefinition/kelvin-history. Retrieved 21 February 2022.
- ↑ "Essay II. On the force of steam or vapour from water and various other liquids, both in vacuum and in air". Memoirs of the Literary and Philosophical Society of Manchester 5 part 2: 550–574. 1801. https://books.google.com/books?id=3qdJAAAAYAAJ&pg=PA595.
- ↑ "Essay IV. On the expansion of elastic fluids by heat". Memoirs of the Literary and Philosophical Society of Manchester 5 part 2: 595–602. 1801. https://books.google.com/books?id=3qdJAAAAYAAJ&pg=PA595.
- ↑ "Recherches sur la dilatation des gaz et des vapeurs", Annales de Chimie XLIII: 137, 1802. English translation (extract).
- ↑ Thomson 1882, pp. 100–106.
- ↑ 14.0 14.1 Magie, William Francis (1935). A Source Book In Physics. p. 237. https://archive.org/details/in.ernet.dli.2015.449479/page/n251/mode/2up.
- ↑ Thomson 1882, p. 104: "If we push the strict principle of graduation, stated above, sufficiently far, we should arrive at a point corresponding to the volume of air being reduced to nothing, which would be marked as −273° of the scale (−100/·366, if ·366 be the coefficient of expansion); and therefore −273° of the air-thermometer is a point which cannot be reached at any finite temperature, however low."
- ↑ Thomson 1882, p. 104.
- ↑ Thomson 1882, p. 187.
- ↑ 18.0 18.1 Thomson 1882, p. 106.
- ↑ Thomson 1882, p. 193.
- ↑ Thomson 1882, p. 212.
- ↑ Thomson 1882, p. 186.
- ↑ Thomson 1882, p. 192.
- ↑ Thomson 1882, pp. 214–215.
- ↑ Thomson 1882, p. 213.
- ↑ Thomson 1882, p. 388.
- ↑ Thomson 1882, p. 105: "The arbitrary points which coincide on the two scales are 0° and 100°"
- ↑ Saslow, WM (7 January 2020). "A History of Thermodynamics: The Missing Manual.". Entropy 22 (1): eqn. (36). doi:10.3390/e22010077. PMID 33285852. Bibcode: 2020Entrp..22...77S.
- ↑ Thomson 1882, p. 190, formula (7).
- ↑ Thomson 1882, pp. 106, 232–236.
- ↑ Thomson 1882, p. 234.
- ↑ Wang, Lin-Shu (2020). A treatise of heat and energy. Cham: Springer. p. 77. ISBN 9783030057466.
- ↑ Thomson 1882, p. 235.
- ↑ Thomson 1882, p. 236.
- ↑ Thomson, James (1873). "A quantitative investigation of certain relations between the gaseous, the liquid, and the solid states of water-substance". Proceedings of the Royal Society of London 22: 28. ISSN 0370-1662. Bibcode: 1873RSPS...22...27T. https://babel.hathitrust.org/cgi/pt?id=hvd.32044106377062&view=1up&seq=48. "and consequently that the three curves would meet or cross each other in one point, which I have called the triple point.".
- ↑ 35.0 35.1 Swinton, F. L. (September 1967). "The triplet point of water" (in en). Journal of Chemical Education 44 (9): 541. doi:10.1021/ed044p541. ISSN 0021-9584. Bibcode: 1967JChEd..44..541S. https://pubs.acs.org/doi/abs/10.1021/ed044p541.
- ↑ "Resolution 3 of the 9th CGPM (1948)". BIPM. https://www.bipm.org/en/committees/cg/cgpm/9-1948/resolution-3.
- ↑ "Resolution 3 of the 10th CGPM (1954)". BIPM. https://www.bipm.org/en/committees/cg/cgpm/10-1954/resolution-3.
- ↑ "Resolution 3: Definition of the thermodynamic temperature scale". Resolutions of the 10th CGPM. Bureau International des Poids et Mesures. 1954. http://www.bipm.fr/en/CGPM/db/10/3/.
- ↑ 39.0 39.1 "Resolution 3 of the 13th CGPM (1967)". BIPM. https://www.bipm.org/en/committees/cg/cgpm/13-1967/resolution-3.
- ↑ "Resolution 3: SI unit of thermodynamic temperature (kelvin)". Resolutions of the 13th CGPM. Bureau International des Poids et Mesures. 1967. http://www.bipm.fr/en/CGPM/db/13/3/.
- ↑ {{cite book |title=Physikalisches Wörterbuch |language=de |trans-title= |chapter=Nox, Dunkelleuchtdichte, Skot |author-first=Wilhelm Heinrich |author-last=Westphal |editor-first1=Wilhelm H. |editor-last1=Westphal |date=1952 |edition=1 |publisher=Springer-Verlag OHG |publication-place=Berlin / Göttingen / Heidelberg, Germany |isbn=978-3-662-12707-0 |doi=10.1007/978-3-662-12706-3 |pages=125, 271, 389 |chapter-url=https://books.google.com/books?id=QaCFBwAAQBAJ&pg=RA1-PA125 |access-date=2023-03-16 |quote-pages=271, 389 |quote=Dunkelleuchtdichte. [...] Unter Zugrundelegung dieser Empfindlichkeitskurve hat man 1940 in Deutschland die Dunkelleuchtdichte mit der Einheit Skot (sk) so festgesetzt, daß bei einem Licht der Farbtemperatur 2360 °K 1 sk = 10−3 asb gilt. 1948 ist von der Internationalen Beleuchtungskommission (IBK) die Bezugstemperatur auf 2046 , die Erstarrungstemperatur des Platins, festgesetzt worden. Die Bezeichnung Skot wurde von der IBK nicht übernommen, dafür soll "skotopisches Stilb" gesagt werden. Als höchstzulässiger Grenzwert für die Dunkelleuchtdichte ist in Deutschland 10 Skot festgesetzt worden, um eine Verwendung der Dunkelleuchtdichte im Gebiet des gemischten Zapfen- und Stäbchensehens zu vermeiden, da in diesem Bereich die photometrischen Maßgrößen wegen der allmählich gleitenden Augenempfindlichkeitskurve ihren Sinn verlieren. [...] Skot, abgek[ürzt] sk, Einheit für die Dunkelleuchtdichte, welche für zahlenmäßige Angaben und zum Anschluß der Dunkelleuchtdichte an die normale Leuchtdichte 1940 von der German Lighting Society (de) geschaffen wurde. Für diesen Anschluß wurde die Strahlung des schwarzen Körpers bei T = 2360
- ↑ "Resolution 4 of the 13th CGPM (1967)". BIPM. https://www.bipm.org/en/committees/cg/cgpm/13-1967/resolution-4.
- ↑ "Resolution 4: Definition of the SI unit of thermodynamic temperature (kelvin)". Resolutions of the 13th CGPM. Bureau International des Poids et Mesures. 1967. https://www.bipm.org/en/CGPM/db/13/4/.
- ↑ "Resolution 10 of the 23rd CGPM (2007)". BIPM. https://www.bipm.org/en/committees/cg/cgpm/23-2007/resolution-10.
- ↑ "Unit of thermodynamic temperature (kelvin)". SI Brochure, 8th edition. Bureau International des Poids et Mesures. 1967. Section 2.1.1.5. http://www1.bipm.org/en/si/si_brochure/chapter2/2-1/2-1-1/kelvin.html.
- ↑ 46.0 46.1 46.2 Kalinin, M.; Kononogov, S. (2005). "Boltzmann's Constant, the Energy Meaning of Temperature, and Thermodynamic Irreversibility". Measurement Techniques 48 (7): 632–636. doi:10.1007/s11018-005-0195-9. Bibcode: 2005MeasT..48..632K.
- ↑ Kittel, Charles; Kroemer, Herbert (1980). Thermal physics (2nd ed.). San Francisco: W. H. Freeman. pp. 41. ISBN 0716710889. "We prefer to use a more natural temperature scale ... the fundamental temperature has the units of energy."
- ↑ 48.0 48.1 "Report to the CIPM on the implications of changing the definition of the base unit Kelvin". International Committee for Weights and Measures (CIPM). 2007-05-02. http://www.bipm.org/wg/CCT/TG-SI/Allowed/Documents/Report_to_CIPM_2.pdf.
- ↑ 49.0 49.1 Ian Mills (29 September 2010). "Draft Chapter 2 for SI Brochure, following redefinitions of the base units". CCU. http://www.bipm.org/utils/en/pdf/si_brochure_draft_ch2.pdf.
- ↑ "General Conference on Weights and Measures approves possible changes to the International System of Units, including redefinition of the kilogram" (PDF) (Press release). Sèvres, France: General Conference on Weights and Measures. 23 October 2011. Archived from the original (PDF) on 9 February 2012. Retrieved 25 October 2011.
- ↑ Wood, B. (3–4 November 2014). "Report on the Meeting of the CODATA Task Group on Fundamental Constants". p. 3. http://www.bipm.org/cc/TGFC/Allowed/Minutes/CODATA_Minutes_14-BIPM-public.pdf. "Molar gas constant R and Boltzmann constant k"
- ↑ "2018 CODATA Value: Boltzmann constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?k. Retrieved 2019-05-20.
- ↑ 53.0 53.1 "Resolution 1 of the 26th CGPM (2018)". BIPM. https://www.bipm.org/en/committees/cg/cgpm/26-2018/resolution-1.
- ↑ "Updating the definition of the kelvin". BIPM. http://www.bipm.org/wg/CCT/TG-SI/Allowed/Documents/Updating_the_definition_of_the_kelvin2.pdf.
- ↑ Newell, D B; Cabiati, F; Fischer, J; Fujii, K; Karshenboim, S G; Margolis, H S; de Mirandés, E; Mohr, P J et al. (29 January 2018). "The CODATA 2017 values of h, e, k, and NA for the revision of the SI". Metrologia 55 (1): L13–L16. doi:10.1088/1681-7575/aa950a. Bibcode: 2018Metro..55L..13N.
- ↑ Fischer, J; Fellmuth, B; Gaiser, C; Zandt, T; Pitre, L; Sparasci, F; Plimmer, M D; de Podesta, M et al. (1 April 2018). "The Boltzmann project". Metrologia 55 (2): R1–R20. doi:10.1088/1681-7575/aaa790. PMID 31080297. Bibcode: 2018Metro..55R...1F.
- ↑ Mohr, Peter J.; Shirley, Eric L.; Phillips, William D.; Trott, Michael (1 October 2022). "On the dimension of angles and their units". Metrologia 59 (5): 053001. doi:10.1088/1681-7575/ac7bc2. Bibcode: 2022Metro..59e3001M. "The scientific community could have decided to have a unit system in which temperature is measured in joules, but we find it to be more convenient to measure temperature in kelvins.".
- ↑ Fellmuth, B.; Fischer, J.; Machin, G.; Picard, S.; Steur, P. P. M.; Tamura, O.; White, D. R.; Yoon, H. (28 March 2016). "The kelvin redefinition and its mise en pratique". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 374 (2064). doi:10.1098/rsta.2015.0037.
- ↑ Ostlie, Dale A. (2022). Astronomy: The Human Quest for Understanding. Oxford University Press. ISBN 978-0-19-882582-1. https://books.google.com/books?id=zT2HEAAAQBAJ&pg=PA216.
- ↑ "Sun Fact Sheet". https://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html.
- ↑ Falkner, David E. (2 September 2021). Stories of Astronomers and Their Stars. Springer. ISBN 978-3-030-80309-4. https://books.google.com/books?id=2QBBEAAAQBAJ&dq=5772+K&pg=PA51.
- ↑ Prša, Andrej; Harmanec, Petr; Torres, Guillermo; Mamajek, Eric; Asplund, Martin; Capitaine, Nicole; Christensen-Dalsgaard, Jørgen; Depagne, Éric et al. (2016). "NOMINAL VALUES FOR SELECTED SOLAR AND PLANETARY QUANTITIES: IAU 2015 RESOLUTION B3* †". The Astronomical Journal 152 (2): 41. doi:10.3847/0004-6256/152/2/41.
- ↑ "NIST Guide to the SI | Chapter 9: Rules and Style Conventions for Spelling Unit Names", NIST SP 811, 28 January 2016, https://www.nist.gov/pml/special-publication-811/nist-guide-si-chapter-9-rules-and-style-conventions-spelling-unit-names#97, "A derived unit is usually singular in English, for example, the value 3 m2·K/W is usually spelled out as 'three square meter kelvin per watt', and the value 3 C·m2/V is usually spelled out as 'three coulomb meter squared per volt'. However, a 'single' unit may be plural; for example, the value 5 kPa is spelled out as 'five kilopascals', although 'five kilopascal' is acceptable. If in such a single-unit case the number is less than one, the unit is always singular when spelled out; for example, 0.5 kPa is spelled out as 'five-tenths kilopascal'."
- ↑ "Definition of KELVIN". https://www.merriam-webster.com/dictionary/kelvin.
- ↑ CERN English Language Style Guide. CERN. 2022. pp. 64. https://translation-council-support-group.web.cern.ch/sites/default/files/styles/large/CERN%20TM%20English%20language%20style%20guide.pdf.
- ↑ "Writing with SI (Metric System) Units". NIST. 2010-01-13. https://www.nist.gov/pml/owm/writing-si-metric-system-units.
- ↑ Brady, James E.; Senese, Fred (28 January 2008). Chemistry, Student Study Guide: The Study of Matter and Its Changes. John Wiley & Sons. p. 15. ISBN 978-0-470-18464-6. https://books.google.com/books?id=zS1EX-e7kPQC&pg=PA15.
- ↑ The Unicode Standard, Version 8.0. Mountain View, California, US: The Unicode Consortium. August 2015. ISBN 978-1-936213-10-8. https://www.unicode.org/versions/Unicode8.0.0/ch22.pdf. Retrieved 6 September 2015.
Bibliography
- Bureau International des Poids et Mesures (2019). "The International System of Units (SI) Brochure". International Committee for Weights and Measures. https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf.
- Thomson, William (Lord Kelvin) (1882). Mathematical and physical papers: Volume I. Cambridge University Press. https://archive.org/details/mathematicalphys01kelv.
External links
- "On an Absolute Thermometric Scale founded on Carnot's Theory of the Motive Power of Heat, and calculated from Regnault's Observations". Philosophical Magazine. October 1848. https://zapatopi.net/kelvin/papers/on_an_absolute_thermometric_scale.html.
- "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam". Transactions of the Royal Society of Edinburgh. March 1851. https://zapatopi.net/kelvin/papers/on_the_dynamical_theory_of_heat.html.
 |

