Physics:Gamow factor

Short description: Chance of overcoming the Coulomb barrier

Tunnelling probability (filled curve) as a function of energy. Left-most curve is the Maxwell–Boltzmann factor and right-most curve is Gamow's factor. 'Δ' indicates the Gamow window - is $\propto T^{5/6}$ (T is the temperature).

The Gamow factor, Sommerfeld factor or Gamow–Sommerfeld factor, named after physicists George Gamow and Arnold Sommerfeld, is a probability factor for two nuclear particles' chance of overcoming the Coulomb barrier in order to undergo nuclear reactions, for example in nuclear fusion. By classical physics, there is almost no possibility for protons to fuse by crossing each other's Coulomb barrier at temperatures commonly observed to cause fusion, such as those found in the Sun. In 1927 it was discovered that there is a significant chance for nuclear fusion due to quantum tunnelling.

While the probability of overcoming the Coulomb barrier increases rapidly with increasing particle energy, for a given temperature, the probability of a particle having such an energy falls off very fast, as described by the Maxwell–Boltzmann distribution. Gamow found that, taken together, these effects mean that for any given temperature, the particles that fuse are mostly in a temperature-dependent narrow range of energies known as the Gamow window. The maximum of the distribution is called the Gamow peak.

Description

The probability of two nuclear particles overcoming their electrostatic barriers is given by the following factor:

$P_{\text{G}}(E)=e^{-\sqrt{E_{\text{G}}/E}},$

where $E_{\text{G}}$ is the Gamow energy

$E_{\text{G}}\equiv 2\mu c^2(\pi \alpha Z_{\text{a}}{Z}_{\text{b}}{)}^2,$

where $\mu =\frac{m_{\text{a}}{m}_{\text{b}}}{m_{\text{a}}+m_{\text{b}}}$ is the reduced mass of the two particles. The constant $\alpha$ is the fine-structure constant, $c$ is the speed of light, and $Z_{\text{a}}$ and $Z_{\text{b}}$ are the respective atomic numbers of each particle.

It is sometimes rewritten using the Sommerfeld parameter η, such that

$P_{\text{G}}(E)=e^{-2\pi \eta },$

where η is a dimensionless quantity used in nuclear astrophysics in the calculation of reaction rates between two nuclei and it also appears in the definition of the astrophysical S-factor. It is defined as

$\eta =\frac{Z_a{Z}_b{e}^2}{4\pi {ϵ}_0\hslash v}=\alpha Z_1{Z}_2\sqrt{\frac{\mu c^2}{2E}},$

where e is the elementary charge, v is the magnitude of the relative incident velocity in the centre-of-mass frame.

Derivation

Top (black): Scheme of an energy barrier of height U as function of position. Bottom (red): Schrödinger wave-function with energy E.

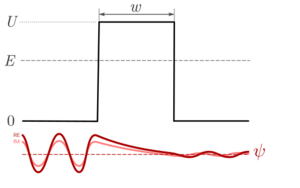
1D problem

The derivation consists in the one-dimensional case of quantum tunnelling using the WKB approximation. Considering a wave function of a particle of mass m, we take area 1 to be where a wave is emitted, area 2 the potential barrier which has height V and width l (at $0<x<l$), and area 3 its other side, where the wave is arriving, partly transmitted and partly reflected. For wave numbers k [m⁻¹] and energy E we get:

${\mathrm{\Psi }}_1=A{e}^{i(kx+\alpha )}{e}^{-iEt/\hslash }$

${\mathrm{\Psi }}_2=B_1{e}^{-k^{\prime }x}+B_2{e}^{k^{\prime }x}$

${\mathrm{\Psi }}_3=(C_1{e}^{-i(kx+\beta )}+C_2{e}^{i(kx+{\beta }^{\prime })})\cdot e^{-iEt/\hslash }$

where $k=\sqrt{2mE/{\hslash }^2}$ and $k^{\prime }=\sqrt{2m(V-E)/{\hslash }^2},$ both in [1/m]. This is solved for given A and phase α by taking the boundary conditions at the barrier edges, at $x=0$ and $x=l$: there ${\mathrm{\Psi }}_{1,3}(t)$ and its derivatives must be equal on both sides. For $k^{\prime }l\gg 1$, this is easily solved by ignoring the time exponential and considering the real part alone (the imaginary part has the same behaviour). We get, up to factors

• depending on the β phases which are typically of order 1, and
• of the order of $k/k^{\prime }=\sqrt{E/(V-E)}$ (assumed not very large, since V is greater than E (not marginally)):

${\mathrm{\Psi }}_1=A{e}^{i(kx+\alpha )},{\mathrm{\Psi }}_3=C_1{e}^{-i(kx+\beta )}+C_2{e}^{i(kx+{\beta }^{\prime })},$

${\mathrm{\Psi }}_2\approx A{e}^{-k^{\prime }x}+A{e}^{k^{\prime }x}:B_1,B_2\approx A$ and $C_1,C_2\approx \frac{1}{2}A\frac{k^{\prime }}{k}{e}^{k^{\prime }l}.$

Next, the alpha decay can be modelled as a symmetric one-dimensional problem, with a standing wave between two symmetric potential barriers at $q_0<x<q_0+l$ and $-(q_0+l)<x<-q_0$, and emitting waves at both outer sides of the barriers. Solving this can in principle be done by taking the solution of the first problem, translating it by $q_0$ and gluing it to an identical solution reflected around $x=0$.

Alpha decay modelled as two symmetrical Coulomb potential barriers in 1D.

Due to the symmetry of the problem, the emitting waves on both sides must have equal amplitudes (A), but their phases (α) may be different. This gives a single extra parameter; however, gluing the two solutions at $x=0$ requires two boundary conditions (for both the wave function and its derivative), so in general there is no solution. In particular, re-writing ${\mathrm{\Psi }}_3$ (after translation by $q_0$) as a sum of a cosine and a sine of $kx$, each having a different factor that depends on k and β; the factor of the sine must vanish, so that the solution can be glued symmetrically to its reflection. Since the factor is in general complex (hence its vanishing imposes two constraints, representing the two boundary conditions), this can in general be solved by adding an imaginary part of k, which gives the extra parameter needed. Thus E will have an imaginary part as well.

The physical meaning of this is that the standing wave in the middle decays; the waves newly emitted have therefore smaller amplitudes, so that their amplitude decays in time but grows with distance. The decay constant, denoted λ [1/s], is assumed small compared to $E/\hslash$.

λ can be estimated without solving explicitly, by noting its effect on the probability current conservation law. Since the probability flows from the middle to the sides, we have:

$\frac{\partial }{\partial t}\underset{-(q_0+l)}{\overset{(q_0+l)}{\int }}{\mathrm{\Psi }}^{*}\mathrm{\Psi }dx=2\frac{\hslash }{2mi}({\mathrm{\Psi }}_1^{*}\frac{\partial {\mathrm{\Psi }}_1}{\partial x}-{\mathrm{\Psi }}_1\frac{\partial {\mathrm{\Psi }}_1^{*}}{\partial x}),$

note the factor of 2 is due to having two emitted waves.

Taking $\mathrm{\Psi }\sim e^{-\lambda t}$, this gives:

$\lambda \frac{2}{4}(q_0+l){\left(A\frac{k^{\prime }}{k}\right)}^2{e}^{2k^{\prime }l}\approx 2\frac{\hslash }{m}{A}^{2}k.$

Since the quadratic dependence on $k^{\prime }l$ is negligible relative to its exponential dependence, we may write:

$\lambda \approx 4\frac{\hslash k}{m(q_0+l)}\frac{k^2}{k{\text{'}}^2}\cdot e^{-2k^{\prime }l}.$

Remembering the imaginary part added to k is much smaller than the real part, we may now neglect it and get:

$\lambda \approx 4\frac{\hslash k}{m(q_0+l)}\cdot \frac{E}{V-E}\cdot e^{-2\sqrt{2m(V-E)}l/\hslash }.$

Note that $\frac{\hslash k}{m}=\sqrt{2E/m}$ is the particle velocity, so the first factor is the classical rate by which the particle trapped between the barriers ($2q_0$ apart) hits them.

3D problem

Scheme of the potential barrier in radial coordinates.

Finally, moving to the three-dimensional problem, the spherically symmetric Schrödinger equation reads (expanding the wave function $\psi (r,\theta ,\varphi )=\chi (r)u(\theta ,\varphi )$ in spherical harmonics and looking at the l-th term):

$\frac{{\hslash }^2}{2m}(\frac{d^2\chi }{d{r}^2}+\frac{2}{r}\frac{d\chi }{dr})=(V(r)+\frac{{\hslash }^2}{2m}\frac{\ell (\ell +1)}{r^2}-E)\chi .$

Since $\ell >0$ amounts to enlarging the potential, and therefore substantially reducing the decay rate (given its exponential dependence on $\sqrt{V-E}$): we focus on $\ell =0$, and get a very similar problem to the previous one with $\chi (r)=\mathrm{\Psi }(r)/r$, except that now the potential as a function of r is not a step function. In short $\frac{{\hslash }^2}{2m}(\ddot{\chi }+\frac{2}{r}\dot{\chi })=(V(r)-E)\chi .$

The main effect of this on the amplitudes is that we must replace the argument in the exponent, taking an integral of $2\sqrt{2m(V-E)}/\hslash$ over the distance where $V(r)>E$ rather than multiplying by width l. We take the Coulomb potential:

$V(r)=\frac{z(Z-z)e^2}{4\pi {\epsilon }_{0}r}$

where ${\epsilon }_0$ is the vacuum electric permittivity, e the electron charge, z = 2 is the charge number of the alpha particle and Z the charge number of the nucleus (Z–z after emitting the particle). The integration limits are then:

$r_2=\frac{z(Z-z)e^2}{4\pi {\epsilon }_{0}E},$ where we assume the nuclear potential energy is still relatively small, and

$r_1$, which is where the nuclear negative potential energy is large enough so that the overall potential is smaller than E.

Thus, the argument of the exponent in λ is:

$2\frac{\sqrt{2mE}}{\hslash }\underset{r_1}{\overset{r_2}{\int }}\sqrt{\frac{V(r)}{E}-1}dr=2\frac{\sqrt{2mE}}{\hslash }\underset{r_1}{\overset{r_2}{\int }}\sqrt{\frac{r_2}{r}-1}dr.$

This can be solved by substituting $t=\sqrt{r/r_2}$ and then $t=\cos (\theta )$ and solving for θ, giving:

$2r_2\frac{\sqrt{2mE}}{\hslash }[{\cos }^{-1}(\sqrt{x})-\sqrt{x}\sqrt{1-x}]=2\frac{\sqrt{2m}z(Z-z)e^2}{4\pi {\epsilon }_0\hslash \sqrt{E}}[{\cos }^{-1}(\sqrt{x})-\sqrt{x}\sqrt{1-x}]$

where $x=r_1/r_2$. Since x is small, the x-dependent factor is of the order 1.

Assuming

$x\ll 1$

, the x-dependent factor can be replaced by

$\arccos 0=\pi /2,$

giving:

$\lambda \approx e^{-\sqrt{E_{\mathrm{G}}/E}}$

with

$E_{\mathrm{G}}=\frac{{\pi }^{2}m/2{[z(Z-z)e^2]}^2}{(4\pi {\epsilon }_0\hslash {)}^2}.$

Which is the same as the formula given in the beginning of the article with

$Z_{\text{a}}=z$

,

$Z_{\text{b}}=Z-z$

and the fine-structure constant

$\alpha =\frac{e^2}{4\pi {\epsilon }_0\hslash c}:\sqrt{E_{\mathrm{G}}}=\sqrt{m/2}/(4{ϵ}_0\hslash )[Z_{a}e{Z}_{b}e].$

For a radium alpha decay, Z = 88, z = 2 and m ≈ 4m_p, E_G is approximately 50 GeV. Gamow calculated the slope of $\log (\lambda )$ with respect to E at an energy of 5 MeV to be ~ 10¹⁴ J⁻¹, compared to the experimental value of 0.7×10¹⁴ J⁻¹.

Gamow peak

For an ideal gas, the Maxwell–Boltzmann distribution is proportional to

$P_{\text{MB}}(E)\propto e^{-m⟨v^2⟩/2k_{\mathrm{B}}T}=e^{-E/k_{\mathrm{B}}T}$

where $⟨v^2⟩$ is the average squared speed of all particles, $k_{\mathrm{B}}$ is the Boltzmann constant and T is absolute temperature.

The fusion probability is the product of the Maxwell–Boltzmann distribution factor and the Gamow factor

$P_{\text{fusion}}(E)=P_{\text{MB}}(E)\cdot P_{\text{G}}(E)=\exp (-\frac{E}{k_{\mathrm{B}}T}-\sqrt{\frac{E_{\mathrm{G}}}{E}})$

The maximum of the fusion probability is given by $\partial P_{\text{fusion}}/\partial E=0,$ which yields

$E_{\mathrm{m}\mathrm{a}\mathrm{x}}={\left[E_{\mathrm{G}}{\left(\frac{k_{\mathrm{B}}T}{2}\right)}^2\right]}^{1/3}.$

This quantity is known as the Gamow peak.

Expanding $P_{\text{fusion}}$ around $E_{\mathrm{m}\mathrm{a}\mathrm{x}}$ gives:

$P_{\text{fusion}}(E)\approx P_{\text{fusion}}(E_{\text{max}})\cdot [1+{\left(\frac{E-E_{\mathrm{m}\mathrm{a}\mathrm{x}}}{2\mathrm{\Delta }}\right)}^2+\cdots ],$

where (in joule)

$\mathrm{\Delta }(T)=4\sqrt{\frac{E_{\mathrm{m}\mathrm{a}\mathrm{x}}{k}_{\mathrm{B}}T}{3}}=\frac{2^{5/3}}{\sqrt{3}}[E_{\mathrm{G}}^{}(k_{\mathrm{B}}T{)}^5{]}^{1/6}$

is the Gamow window.

History

In 1927, Ernest Rutherford published an article in Philosophical Magazine on a problem related to Hans Geiger's 1921 experiment of scattering alpha particles from uranium. Previous experiments with thorium C' (now called polonium-262) confirmed that uranium has a Coulomb barrier of 8.57 MeV, however uranium emitted alpha particles of 4.2 MeV. The emitted energy was too low to overcome the barrier. On 29 July 1928, George Gamow, and independently the next day Ronald Wilfred Gurney and Edward Condon submitted their solution based on quantum tunnelling to the journal Zeitschrift für Physik. Their work was based on previous work on tunnelling by J. Robert Oppenheimer, Gregor Wentzel, Lothar Wolfgang Nordheim, and Ralph H. Fowler. Gurney and Condon cited also Friedrich Hund.

In 1931, Arnold Sommerfeld introduced a similar factor (a Gaunt factor) for the discussion of bremsstrahlung.

Gamow popularized his personal version of the discovery in his 1970's book, My World Line: An Informal Autobiography.

See also

• Stellar nucleosynthesis

External links

• Modeling Alpha Half-life (Georgia State University) hyperphysics.phy-astr.gsu.edu