Physics:Quantum tunnelling
| Part of a series on |
| Quantum mechanics |
|---|
In physics, quantum tunnelling, barrier penetration, or simply tunnelling is a quantum mechanical phenomenon in which an object such as an electron or atom passes through a potential energy barrier that, according to classical mechanics, should not be passable due to the object not having sufficient energy to pass or surmount the barrier.
Tunnelling is a consequence of the wave nature of matter and quantum indeterminacy. The quantum wave function describes the states of a particle or other physical system and wave equations such as the Schrödinger equation describe their evolution. In a system with a short, narrow potential barrier, a small part of wavefunction can appear outside of the barrier representing a probability for tunnelling through the barrier.
Since the probability of transmission of a wave packet through a barrier decreases exponentially with the barrier height, the barrier width, and the tunnelling particle's mass, tunnelling is seen most prominently in low-mass particles such as electrons tunnelling through atomically narrow barriers. However tunnelling has been observed with protons and even atoms and tunnelling has been used to explain physical effects with particles this large.
Tunnelling plays an essential role in physical phenomena such as nuclear fusion[1] and alpha radioactive decay of atomic nuclei. Tunnelling applications include the tunnel diode,[2] quantum computing, flash memory, and the scanning tunnelling microscope. Tunnelling limits the minimum size of devices used in microelectronics because electrons tunnel readily through insulating layers and transistors that are thinner than about 1 nm.[3]
The effect was predicted in the early 20th century. Its acceptance as a general physical phenomenon came mid-century.[4]
Concept
File:Quantum tunnel effect and its application to the scanning tunneling microscope.ogv
Quantum tunnelling falls under the domain of quantum mechanics. To understand the phenomenon, particles attempting to travel across a potential barrier can be compared to a ball trying to roll over a hill. Quantum mechanics and classical mechanics differ in their treatment of this scenario.
Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier cannot reach the other side. Thus, a ball without sufficient energy to surmount the hill would roll back down. In quantum mechanics, a particle can, with a small probability, tunnel to the other side, thus crossing the barrier. The reason for this difference comes from treating matter as having properties of waves and particles.
Some sources describe the mere penetration of a wave function into the barrier, without transmission on the other side, as a tunnelling effect, such as in tunnelling into the walls of a finite potential well.[5][6]
Tunnelling problem
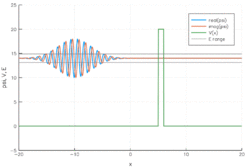
The wave function of a physical system of particles specifies everything that can be known about the system.[7] Therefore, problems in quantum mechanics analyse the system's wave function. Using mathematical formulations, such as the Schrödinger equation, the time evolution of a known wave function can be deduced. The square of the absolute value of this wave function is directly related to the probability distribution of the particle positions, which describes the probability that the particles would be measured at those positions.
As shown in the animation, when a wave packet impinges on the barrier, most of it is reflected and some is transmitted through the barrier. The wave packet becomes more delocalised: it is now on both sides of the barrier and lower in maximum amplitude, but equal in integrated square-magnitude, meaning that the probability the particle is somewhere remains unity. The wider the barrier and the higher the barrier energy, the lower the probability of tunnelling.
Some models of a tunnelling barrier, such as the rectangular barriers shown, can be analysed and solved algebraically.[8]: 96 Most problems do not have an algebraic solution, so numerical solutions are used. "Semiclassical methods" offer approximate solutions that are easier to compute, such as the WKB approximation.
History
The Schrödinger equation was published in 1926. The first person to apply the Schrödinger equation to a problem that involved tunnelling between two classically allowed regions through a potential barrier was Friedrich Hund in a series of articles published in 1927. He studied the solutions of a double-well potential and discussed molecular spectra.[9] Leonid Mandelstam and Mikhail Leontovich discovered tunnelling independently and published their results in 1928.[10]
In 1927, Lothar Nordheim, assisted by Ralph Fowler, published a paper that discussed thermionic emission and reflection of electrons from metals. He assumed a surface potential barrier that confines the electrons within the metal and showed that the electrons have a finite probability of tunnelling through or reflecting from the surface barrier when their energies are close to the barrier energy. Classically, the electron would either transmit or reflect with 100% certainty, depending on its energy. In 1928 J. Robert Oppenheimer published two papers on field emission, i.e. the emission of electrons induced by strong electric fields. Nordheim and Fowler simplified Oppenheimer's derivation and found values for the emitted currents and work functions that agreed with experiments.[9]
A great success of the tunnelling theory was the mathematical explanation for alpha decay, which was developed in 1928 by George Gamow and independently by Ronald Gurney and Edward Condon.[11][12][13][14] The latter researchers simultaneously solved the Schrödinger equation for a model nuclear potential and derived a relationship between the half-life of the particle and the energy of emission that depended directly on the mathematical probability of tunnelling. All three researchers were familiar with the works on field emission,[9] and Gamow was aware of Mandelstam and Leontovich's findings.[15]
In the early days of quantum theory, the term tunnel effect was not used, and the effect was instead referred to as penetration of, or leaking through, a barrier. The German term wellenmechanischer Tunneleffekt was used in 1931 by Walter Schottky.[9] The English term tunnel effect entered the language in 1932 when it was used by Yakov Frenkel in his textbook.[9]
In 1957 Leo Esaki demonstrated tunnelling of electrons over a few nanometre wide barrier in a semiconductor structure and developed a diode based on the tunnel effect.[16] In 1960, following Esaki's work, Ivar Giaever showed experimentally that tunnelling also took place in superconductors. The tunnelling spectrum gave direct evidence of the superconducting energy gap. In 1962, Brian Josephson predicted the tunnelling of superconducting Cooper pairs. Esaki, Giaever and Josephson shared the 1973 Nobel Prize in Physics for their works on quantum tunnelling in solids.[17][4]
In 1981, Gerd Binnig and Heinrich Rohrer developed a new type of microscope, called scanning tunnelling microscope, which is based on tunnelling and is used for imaging surfaces at the atomic level. Binnig and Rohrer were awarded the Nobel Prize in Physics in 1986 for their discovery.[18]
In 2025, John Clarke, John M. Martinis and Michel H. Devoret received the Nobel Prize in physics for experiments done in 1984 and 1985 that demonstrated how quantum tunnelling can be observed on a macroscopic scale, involving many particles. They built an electrical circuit with two superconductors, components that can conduct a current without any electrical resistance. They separated these with a thin layer of material that did not conduct any current at all. In this experiment, they showed that they could control and investigate a phenomenon in which all the charged particles in the superconductor behave in unison, as if they are a single particle that fills the entire circuit.[19]
Applications
Tunnelling is used to explain some important macroscopic physical phenomena.
Solid-state physics
Electronics
Tunnelling is a source of current leakage in very-large-scale integration (VLSI) electronics and results in a substantial power drain and heating effects that plague such devices. It is considered the lower limit on how microelectronic device elements can be made.[20] Tunnelling is a fundamental technique used to program the floating gates of flash memory.
Cold emission
Cold emission of electrons is relevant to semiconductors and superconductor physics. It is similar to thermionic emission, where electrons randomly jump from the surface of a metal to follow a voltage bias because they statistically end up with more energy than the barrier, through random collisions with other particles. When the electric field is very large, the barrier becomes thin enough for electrons to tunnel out of the atomic state, leading to a current that varies approximately exponentially with the electric field.[21] These materials are important for flash memory, vacuum tubes, and some electron microscopes.
Tunnel junction
A simple barrier can be created by separating two conductors with a very thin insulator. Tunnelling is readily detectable with potential barriers in thin-film junctions of thickness about 3 nm or smaller for electrons.[22] Josephson junctions take advantage of quantum tunnelling and superconductivity to create the Josephson effect. This has applications in precision measurements of voltages and magnetic fields,[21] as well as the multijunction solar cell.
Tunnel diode
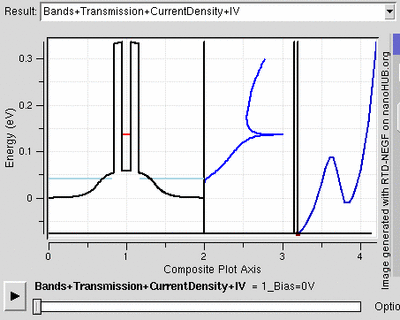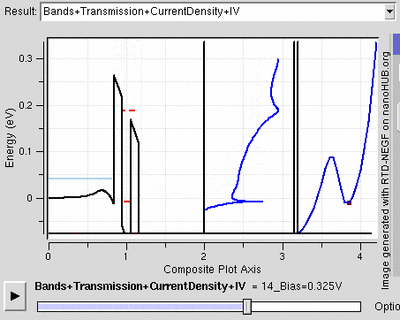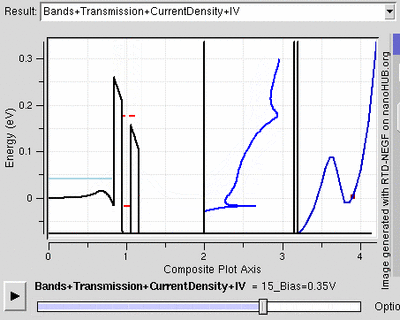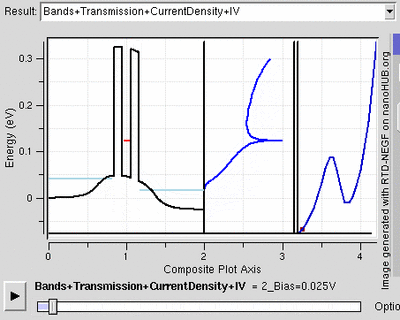
Diodes are electrical semiconductor devices that allow electric current flow in one direction more than the other. The device depends on a depletion layer between N-type and P-type semiconductors to serve its purpose. When these are heavily doped the depletion layer can be thin enough for tunnelling. When a small forward bias is applied, the current due to tunnelling is significant. This has a maximum at the point where the voltage bias is such that the energy level of the valence electrons in the P-side and conduction-band electrons of the N-side are the same. As the voltage bias is increased, the two energy bands no longer line up and the diode acts typically.[23]
Because the tunnelling current drops off rapidly, tunnel diodes can be created that have a range of voltages for which current decreases as voltage increases. This peculiar property is used in some applications, such as high speed devices where the characteristic tunnelling probability changes as rapidly as the bias voltage.[23]
The resonant tunnelling diode makes use of quantum tunnelling in a very different manner to achieve a similar result. This diode has a resonant voltage for which a current favours a particular voltage, achieved by placing two thin layers with a high energy conductance band near each other. This creates a quantum potential well that has a discrete lowest energy level. When this energy level is higher than that of the electrons, no tunnelling occurs and the diode is in reverse bias. Once the two voltage energies align, the electrons flow like an open wire. As the voltage further increases, tunnelling becomes improbable and the diode acts like a normal diode again before a second energy level becomes noticeable.[24]
Tunnel field-effect transistors
A European research project demonstrated field effect transistors in which the gate (channel) is controlled via quantum tunnelling rather than by thermal injection, reducing gate voltage from ≈1 volt to 0.2 volts and reducing power consumption by up to 100×. If these transistors can be scaled up into VLSI chips, they would improve the performance per power of integrated circuits.[25][26]
Conductivity of crystalline solids
While the Drude-Lorentz model of electrical conductivity makes excellent predictions about the nature of electrons conducting in metals, it can be furthered by using quantum tunnelling to explain the nature of the electron's collisions.[21] When a free electron wave packet encounters a long array of uniformly spaced barriers, the reflected part of the wave packet interferes uniformly with the transmitted one between all barriers so that 100% transmission becomes possible. The theory predicts that if positively charged nuclei form a perfectly rectangular array, electrons will tunnel through the metal as free electrons, leading to extremely high conductance, and that impurities in the metal will disrupt it.[21]
Scanning tunnelling microscope
The scanning tunnelling microscope (STM), invented by Gerd Binnig and Heinrich Rohrer, may allow imaging of individual atoms on the surface of a material.[21] It operates by taking advantage of the relationship between quantum tunnelling with distance. When the tip of the STM's needle is brought close to a conduction surface that has a voltage bias, measuring the current of electrons that are tunnelling between the needle and the surface reveals the distance between the needle and the surface. By using piezoelectric rods that change in size when voltage is applied, the height of the tip can be adjusted to keep the tunnelling current constant. The time-varying voltages that are applied to these rods can be recorded and used to image the surface of the conductor.[21] STMs are accurate to 0.001 nm, or about 1% of atomic diameter.[24]
Nuclear physics
Nuclear fusion
Quantum tunnelling is an essential phenomenon for nuclear fusion. The temperature in stellar cores is generally insufficient to allow atomic nuclei to overcome the Coulomb barrier and achieve thermonuclear fusion. Quantum tunnelling increases the probability of penetrating this barrier. Though this probability is still low, the extremely large number of nuclei in the core of a star is sufficient to sustain a steady fusion reaction.[27]
Radioactive decay
Radioactive decay is the process of emission of particles and energy from the unstable nucleus of an atom to form a stable product. This is done via the tunnelling of a particle out of the nucleus (an electron tunnelling into the nucleus is electron capture). This was the first application of quantum tunnelling. Radioactive decay is a relevant issue for astrobiology as this consequence of quantum tunnelling creates a constant energy source over a large time interval for environments outside the circumstellar habitable zone where insolation would not be possible (subsurface oceans) or effective.[27]
Quantum tunnelling may be one of the mechanisms of hypothetical proton decay.[28][29]
Chemistry
Energetically forbidden reactions
Chemical reactions in the interstellar medium occur at extremely low energies. Probably the most fundamental ion-molecule reaction involves hydrogen ions with hydrogen molecules. The quantum mechanical tunnelling rate for the same reaction using the hydrogen isotope deuterium, , has been measured experimentally in an ion trap. The deuterium was placed in an ion trap and cooled. The trap was then filled with hydrogen. At the temperatures used in the experiment, the energy barrier for reaction would not allow the reaction to succeed with classical dynamics alone. Quantum tunnelling allowed reactions to happen in rare collisions. It was calculated from the experimental data that collisions happened one in every hundred billion.[30]
Kinetic isotope effect
In chemical kinetics, the substitution of a light isotope of an element with a heavier one typically results in a slower reaction rate. This is generally attributed to differences in the zero-point vibrational energies for chemical bonds containing the lighter and heavier isotopes and is generally modelled using transition state theory. However, in certain cases, large isotopic effects are observed that cannot be accounted for by a semi-classical treatment, and quantum tunnelling is required. R. P. Bell developed a modified treatment of Arrhenius kinetics that is commonly used to model this phenomenon.[31]
Astrochemistry in interstellar clouds
By including quantum tunnelling, the astrochemical syntheses of various molecules in interstellar clouds can be explained, such as the synthesis of molecular hydrogen, water (ice) and the prebiotic important formaldehyde.[27] Tunnelling of molecular hydrogen has been observed in the lab.[30]
Biology
Quantum tunnelling is among the central non-trivial quantum effects in quantum biology.[32] Here it is important both as electron tunnelling and proton tunnelling. Electron tunnelling is a key factor in many biochemical redox reactions (photosynthesis, cellular respiration) as well as enzymatic catalysis. Proton tunnelling is a key factor in spontaneous DNA mutation.[27]
Spontaneous mutation occurs when normal DNA replication takes place after a particularly significant proton has tunnelled.[33] A hydrogen bond joins DNA base pairs. A double well potential along a hydrogen bond separates a potential energy barrier. It is believed that the double well potential is asymmetric, with one well deeper than the other such that the proton normally rests in the deeper well. For a mutation to occur, the proton must have tunnelled into the shallower well. The proton's movement from its regular position is called a tautomeric transition. If DNA replication takes place in this state, the base pairing rule for DNA may be jeopardised, causing a mutation.[34] Per-Olov Lowdin was the first to develop this theory of spontaneous mutation within the double helix. Other instances of quantum tunnelling-induced mutations in biology are believed to be a cause of ageing and cancer.[35]
Astrophysics
Quantum tunnelling is expected to occur at the event horizon of black holes, leading to Hawking radiation. Classically nothing can escape from a black hole, but quantum tunnelling gives a small probability for emission of radiation.[22]: 103
Mathematical discussion

Schrödinger equation
The time-independent Schrödinger equation for one particle in one dimension can be written as or where
- is the reduced Planck constant,
- is the particle mass,
- represents distance measured in the direction of motion of the particle,
- is the Schrödinger wave function,
- is the potential energy of the particle (measured relative to any convenient reference level),
- is the energy of the particle that is associated with motion in the -axis (measured relative to ),
- is a quantity defined by , which has no accepted name in physics.
The solutions of the Schrödinger equation take different forms for different values of , depending on whether is positive or negative. When is constant and negative, then the Schrödinger equation can be written in the form
The solutions of this equation represent travelling waves, with phase-constant or . Alternatively, if is constant and positive, then the Schrödinger equation can be written in the form
The solutions of this equation are rising and falling exponentials in the form of evanescent waves. When varies with position, the same difference in behaviour occurs, depending on whether is negative or positive. It follows that the sign of determines the nature of the medium, with negative corresponding to medium A and positive corresponding to medium B. It thus follows that evanescent wave coupling can occur if a region of positive is sandwiched between two regions of negative , hence creating a potential barrier.
The mathematics of dealing with the situation where varies with is difficult, except in special cases that usually do not correspond to physical reality. A full mathematical treatment appears in the 1965 monograph by Fröman and Fröman. Their ideas have not been incorporated into physics textbooks, but their corrections have little quantitative effect.
WKB approximation
The wave function is expressed as the exponential of a function: where is then separated into real and imaginary parts: where and are real-valued functions.
Substituting the second equation into the first and using the fact that the imaginary part needs to be 0 results in: File:Wigner function for tunnelling.ogv
To solve this equation using the semiclassical approximation, each function must be expanded as a power series in . From the equations, the power series must start with at least an order of to satisfy the real part of the equation; for a good classical limit starting with the highest power of the Planck constant possible is preferable, which leads to and with the following constraints on the lowest order terms, and
At this point two extreme cases can be considered.
Case 1
If the amplitude varies slowly as compared to the phase and which corresponds to classical motion. Resolving the next order of expansion yields
Case 2
If the phase varies slowly as compared to the amplitude, and which corresponds to tunnelling. Resolving the next order of the expansion yields
In both cases it is apparent from the denominator that both these approximate solutions are bad near the classical turning points . Away from the potential hill, the particle acts similar to a free and oscillating wave; beneath the potential hill, the particle undergoes exponential changes in amplitude. By considering the behaviour at these limits and classical turning points a global solution can be made.
To start, a classical turning point, is chosen and is expanded in a power series about :
Keeping only the first order term ensures linearity:
Using this approximation, the equation near becomes a differential equation:
This can be solved using Airy functions as solutions.
Taking these solutions for all classical turning points, a global solution can be formed that links the limiting solutions. Given the two coefficients on one side of a classical turning point, the two coefficients on the other side of a classical turning point can be determined by using this local solution to connect them.
Hence, the Airy function solutions will asymptote into sine, cosine and exponential functions in the proper limits. The relationships between and are and
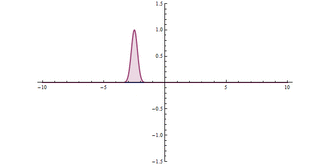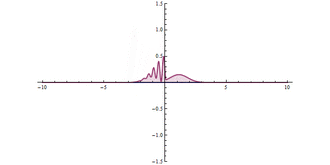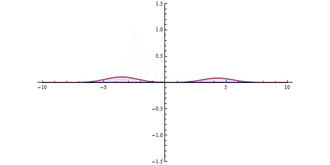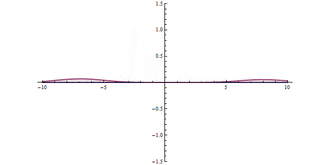
Quantum tunnelling through a barrier. At the origin (), there is a very high, but narrow potential barrier. A significant tunnelling effect can be seen.
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunnelling through a single potential barrier is where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
Faster than light
In 1998, Francis E. Low reviewed briefly the phenomenon of zero-time tunnelling.[36] More recently, experimental tunnelling time data of phonons, photons, and electrons was published by Günter Nimtz.[37] Another experiment overseen by A. M. Steinberg, seems to indicate that particles could tunnel at apparent speeds faster than light.[38][39]
Other physicists, such as Herbert Winful,[40] disputed these claims. Winful argued that the wave packet of a tunnelling particle propagates locally, so a particle can't tunnel through the barrier non-locally. Winful also argued that the experiments that are purported to show non-local propagation have been misinterpreted. In particular, the group velocity of a wave packet does not measure its speed, but is related to the amount of time the wave packet is stored in the barrier. Moreover, if quantum tunnelling is modelled with the relativistic Dirac equation, well established mathematical theorems imply that the process is completely subluminal.[41][42] It has also been proved[43] that within a relativistic quantum field theory framework, tunnelling cannot be superluminal, even though the group velocity can be larger than the light velocity.
Dynamical tunnelling
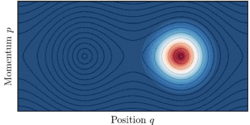
The concept of quantum tunnelling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunnelling.[44][45]
Tunnelling in phase space
The concept of dynamical tunnelling is particularly suited to address the problem of quantum tunnelling in high dimensions (). In the case of an integrable system, where bounded classical trajectories are confined onto tori in phase space, tunnelling can be understood as the quantum transport between semi-classical states built on two distinct but symmetric tori.[46]
Chaos-assisted tunnelling
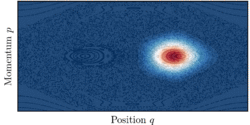
In real life, most systems are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunnelling between them. This phenomenon is referred as chaos-assisted tunnelling.[47] and is characterised by sharp resonances of the tunnelling rate when varying any system parameter.
Resonance-assisted tunnelling
When is small in front of the size of the regular islands, the fine structure of the classical phase space plays a key role in tunnelling. In particular the two symmetric tori are coupled "via a succession of classically forbidden transitions across nonlinear resonances" surrounding the two islands.[48]
Related phenomena
Several phenomena have the same behaviour as quantum tunnelling. Two examples are evanescent wave coupling[49] (the application of Maxwell's wave-equation to light) and the application of the non-dispersive wave-equation from acoustics applied to "waves on strings". These effects are modelled similarly to the rectangular potential barrier. In these cases, one transmission medium through which the wave propagates that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential solutions in medium B.
In optics, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle's total energy is greater than its potential energy and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete. Approximations are useful in this case.
A classical wave-particle association was originally analysed as analogous to quantum tunnelling,[50] but subsequent analysis found a fluid dynamics cause related to the vertical momentum imparted to particles near the barrier.[51]
See also
- Dielectric barrier discharge
- Field electron emission
- Holstein–Herring method
- Proton tunnelling – Type of quantum tunnelling
- Quantum cloning – Process of copying a quantum state with no modification of the original
- Superconducting tunnel junction
- Tunnel diode
- Tunnel junction
- White hole
References
- ↑ Serway; Vuille (2008). College Physics. 2 (Eighth ed.). Belmont: Brooks/Cole. ISBN 978-0-495-55475-2.
- ↑ Taylor, J. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. p. 234. ISBN 978-0-13-805715-2.
- ↑ "Quantum Effects At 7/5nm And Beyond" (in en-US). Semiconductor Engineering. https://semiengineering.com/quantum-effects-at-7-5nm/.
- ↑ 4.0 4.1 Razavy, Mohsen (2003). Quantum Theory of Tunneling. World Scientific. pp. 4, 462. ISBN 978-981-256-488-7. https://archive.org/details/quantumtheoryoft0000raza.
- ↑ Davies, P C W (2004-05-06). "Quantum mechanics and the equivalence principle". Classical and Quantum Gravity 21 (11): 2761–2772. doi:10.1088/0264-9381/21/11/017. ISSN 0264-9381. Bibcode: 2004CQGra..21.2761D. "But quantum particles are able to tunnel into the classically forbidden region ...".
- ↑ Fowler, Michael (5 December 2019). "Particle in a Finite Box and Tunneling". https://chem.libretexts.org/Courses/BethuneCookman_University/B-CU%3ACH-331_Physical_Chemistry_I/CH-331_Text/CH-331_Text/03._The_Schrodinger_Equation_and_a_Particle_In_a_Box/3.09%3A_Particle_in_a_Finite_Box_(and_Tunneling). "Tunneling into the barrier (wall) is possible."
- ↑ Bjorken, James D.; Drell, Sidney D. (1964). Relativistic quantum mechanics. International series in pure and applied physics. New York, NY: McGraw Hill. p. 2. ISBN 978-0-07-005493-6.
- ↑ Messiah, Albert (1966) (in en). Quantum Mechanics. North Holland, John Wiley & Sons. ISBN 0-486-40924-4. https://archive.org/details/quantummechanics0000mess/quantummechanics0000mess.
- ↑ 9.0 9.1 9.2 9.3 9.4 Merzbacher, Eugen (August 2002). "The Early History of Quantum Tunneling". Physics Today 55 (8): 44–49. doi:10.1063/1.1510281. Bibcode: 2002PhT....55h..44M. https://physicstoday.scitation.org/doi/10.1063/1.1510281. Retrieved 17 August 2022. "Friedrich Hund ... was the first to make use of quantum mechanical barrier penetration ...".
- ↑ Mandelstam, L.; Leontowitsch, M. (1928). "Zur Theorie der Schrödingerschen Gleichung". Zeitschrift für Physik 47 (1–2): 131–136. doi:10.1007/BF01391061. Bibcode: 1928ZPhy...47..131M.
- ↑ Gurney, R. W.; Condon, E. U. (1928). "Quantum Mechanics and Radioactive Disintegration". Nature 122 (3073): 439. doi:10.1038/122439a0. Bibcode: 1928Natur.122..439G.
- ↑ Gurney, R. W.; Condon, E. U. (1929). "Quantum Mechanics and Radioactive Disintegration". Physical Review 33 (2): 127–140. doi:10.1103/PhysRev.33.127. Bibcode: 1929PhRv...33..127G.
- ↑ Bethe, Hans (27 October 1966). "Hans Bethe – Session I". Niels Bohr Library & Archives, American Institute of Physics, College Park, Maryland, USA (Interview). Interviewed by Charles Weiner; Jagdish Mehra. Cornell University. Retrieved 1 May 2016.
- ↑ Friedlander, Gerhart; Kennedy, Joseph E.; Miller, Julian Malcolm (1964). Nuclear and Radiochemistry (2nd ed.). New York: John Wiley & Sons. pp. 225–7. ISBN 978-0-471-86255-0. https://archive.org/details/nuclearradiochem00frie.
- ↑ Feinberg, E. L. (2002). "The forefather (about Leonid Isaakovich Mandelstam)". Physics-Uspekhi 45 (1): 81–100. doi:10.1070/PU2002v045n01ABEH001126. Bibcode: 2002PhyU...45...81F.
- ↑ Esaki, Leo (1974-03-22). "Long Journey into Tunneling" (in en). Science 183 (4130): 1149–1155. doi:10.1126/science.183.4130.1149. ISSN 0036-8075. PMID 17789212. Bibcode: 1974Sci...183.1149E. https://www.science.org/doi/10.1126/science.183.4130.1149.
- ↑ Dardo, M. (Mauro) (2004). Nobel laureates and twentieth-century physics. Internet Archive. Cambridge, UK; New York : Cambridge University Press. ISBN 978-0-521-83247-2. http://archive.org/details/nobellaureatestw0000dard.
- ↑ Binnig, Gerd; Rohrer, Heinrich (July 1987). "Scanning tunneling microscopy—from birth to adolescence" (in en). Reviews of Modern Physics 59 (3): 615–625. doi:10.1103/RevModPhys.59.615. ISSN 0034-6861. Bibcode: 1987RvMP...59..615B.
- ↑ Davour, Anna (2025-10-08). "Quantum properties on a human scale" (PDF) (Press release). The Royal Swedish Academy of Sciences. Retrieved 2025-10-08.
- ↑ "Applications of tunneling". http://psi.phys.wits.ac.za/teaching/Connell/phys284/2005/lecture-02/lecture_02/node13.html.
- ↑ 21.0 21.1 21.2 21.3 21.4 21.5 Taylor, J. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. p. 479. ISBN 978-0-13-805715-2.
- ↑ 22.0 22.1 Lerner; Trigg (1991). Encyclopedia of Physics (2nd ed.). New York: VCH. p. 1308. ISBN 978-0-89573-752-6. https://archive.org/details/encyclopediaofph00lern/page/1308.
- ↑ 23.0 23.1 Krane, Kenneth (1983). Modern Physics. New York: John Wiley and Sons. p. 423. ISBN 978-0-471-07963-7. https://archive.org/details/modernphysics00kran/page/423.
- ↑ 24.0 24.1 Knight, R. D. (2004). Physics for Scientists and Engineers: With Modern Physics. Pearson Education. p. 1311. ISBN 978-0-321-22369-2.
- ↑ Ionescu, Adrian M.; Riel, Heike (2011). "Tunnel field-effect transistors as energy-efficient electronic switches". Nature 479 (7373): 329–337. doi:10.1038/nature10679. PMID 22094693. Bibcode: 2011Natur.479..329I. https://infoscience.epfl.ch/handle/20.500.14299/73304.
- ↑ Vyas, P. B.; Naquin, C.; Edwards, H.; Lee, M.; Vandenberghe, W. G.; Fischetti, M. V. (2017-01-23). "Theoretical simulation of negative differential transconductance in lateral quantum well nMOS devices". Journal of Applied Physics 121 (4): 044501. doi:10.1063/1.4974469. ISSN 0021-8979. Bibcode: 2017JAP...121d4501V. https://aip.scitation.org/doi/10.1063/1.4974469.
- ↑ 27.0 27.1 27.2 27.3 Trixler, F. (2013). "Quantum tunnelling to the origin and evolution of life". Current Organic Chemistry 17 (16): 1758–1770. doi:10.2174/13852728113179990083. PMID 24039543.
- ↑ Talou, P.; Carjan, N.; Strottman, D. (1998). "Time-dependent properties of proton decay from crossing single-particle metastable states in deformed nuclei". Physical Review C 58 (6): 3280–3285. doi:10.1103/PhysRevC.58.3280. Bibcode: 1998PhRvC..58.3280T.
- ↑ "adsabs.harvard.edu". http://adsabs.harvard.edu/pdf/1982ApJ...252....1D.
- ↑ 30.0 30.1 Wild, Robert; Nötzold, Markus; Simpson, Malcolm; Tran, Thuy Dung; Wester, Roland (2023-03-16). "Tunnelling measured in a very slow ion–molecule reaction" (in en). Nature 615 (7952): 425–429. doi:10.1038/s41586-023-05727-z. ISSN 0028-0836. PMID 36859549. Bibcode: 2023Natur.615..425W. https://www.nature.com/articles/s41586-023-05727-z.
- ↑ Bell, Ronald Percy (1980). The tunnel effect in chemistry. London: Chapman and Hall. ISBN 0-412-21340-0. OCLC 6854792.
- ↑ Trixler, F. (2013). "Quantum Tunnelling to the Origin and Evolution of Life". Current Organic Chemistry 17 (16): 1758–1770. doi:10.2174/13852728113179990083. PMID 24039543.
- ↑ Matta, Cherif F. (2014). Quantum Biochemistry: Electronic Structure and Biological Activity. Weinheim: Wiley-VCH. ISBN 978-3-527-62922-0. https://books.google.com/books?id=a4JhVFaUOjgC.
- ↑ Majumdar, Rabi (2011). Quantum Mechanics: In Physics and Chemistry with Applications to Bioloty. Newi: PHI Learning. ISBN 978-81-203-4304-7. https://books.google.com/books?id=IJDvyNVeBiYC.
- ↑ Cooper, W. G. (June 1993). "Roles of Evolution, Quantum Mechanics and Point Mutations in Origins of Cancer". Cancer Biochemistry Biophysics 13 (3): 147–170. PMID 8111728.
- ↑ Low, F. E. (1998). "Comments on apparent superluminal propagation". Annalen der Physik 7 (7–8): 660–661. doi:10.1002/(SICI)1521-3889(199812)7:7/8<660::AID-ANDP660>3.0.CO;2-0. Bibcode: 1998AnP...510..660L.
- ↑ Nimtz, G. (2011). "Tunneling Confronts Special Relativity". Found. Phys. 41 (7): 1193–1199. doi:10.1007/s10701-011-9539-2. Bibcode: 2011FoPh...41.1193N.
- ↑ "Quantum-tunnelling time is measured using ultracold atoms – Physics World". 22 July 2020. https://physicsworld.com/a/quantum-tunnelling-time-is-measured-using-ultracold-atoms/.
- ↑ "Quanta Magazine". 20 October 2020. https://www.quantamagazine.org/quantum-tunnel-shows-particles-can-break-the-speed-of-light-20201020/.
- ↑ Winful, H. G. (2006). "Tunneling time, the Hartman effect, and superluminality: A proposed resolution of an old paradox". Phys. Rep. 436 (1–2): 1–69. doi:10.1016/j.physrep.2006.09.002. Bibcode: 2006PhR...436....1W.
- ↑ Thaller, Bernd (1992) (in en). The Dirac Equation. doi:10.1007/978-3-662-02753-0. ISBN 978-3-642-08134-7. https://link.springer.com/book/10.1007/978-3-662-02753-0.
- ↑ Gavassino, L.; Disconzi, M. M. (2023-03-13). "Subluminality of relativistic quantum tunneling". Physical Review A 107 (3). doi:10.1103/PhysRevA.107.032209. Bibcode: 2023PhRvA.107c2209G. https://link.aps.org/doi/10.1103/PhysRevA.107.032209.
- ↑ Alkhateeb, M.; Matzkin, A. (2025-10-07). "Microcausality and tunneling times in relativistic quantum field theory". Physical Review D 112 (7). doi:10.1103/4sh5-d838. https://doi.org/10.1103/4sh5-d838.
- ↑ Davis, Michael J.; Heller, Eric J. (1981-07-01). "Quantum dynamical tunneling in bound states". The Journal of Chemical Physics 75 (1): 246–254. doi:10.1063/1.441832. ISSN 0021-9606. Bibcode: 1981JChPh..75..246D. https://aip.scitation.org/doi/10.1063/1.441832.
- ↑ Keshavamurthy, Srihari; Schlagheck, Peter (2011-03-09) (in en). Dynamical Tunneling: Theory and Experiment. CRC Press. ISBN 978-1-4398-1666-0. https://books.google.com/books?id=c6HMBQAAQBAJ&q=dynamical+tunneling+theory+and+experiment.
- ↑ Wilkinson, Michael (1986-09-01). "Tunnelling between tori in phase space" (in en). Physica D: Nonlinear Phenomena 21 (2): 341–354. doi:10.1016/0167-2789(86)90009-6. ISSN 0167-2789. Bibcode: 1986PhyD...21..341W.
- ↑ Tomsovic, Steven; Ullmo, Denis (1994-07-01). "Chaos-assisted tunneling". Physical Review E 50 (1): 145–162. doi:10.1103/PhysRevE.50.145. PMID 9961952. Bibcode: 1994PhRvE..50..145T. https://link.aps.org/doi/10.1103/PhysRevE.50.145.
- ↑ Brodier, Olivier; Schlagheck, Peter; Ullmo, Denis (2002-08-25). "Resonance-Assisted Tunneling" (in en). Annals of Physics 300 (1): 88–136. doi:10.1006/aphy.2002.6281. ISSN 0003-4916. Bibcode: 2002AnPhy.300...88B. http://www.sciencedirect.com/science/article/pii/S0003491602962810.
- ↑ Martin, Th.; Landauer, R. (1992-02-01). "Time delay of evanescent electromagnetic waves and the analogy to particle tunneling" (in en). Physical Review A 45 (4): 2611–2617. doi:10.1103/PhysRevA.45.2611. ISSN 1050-2947. PMID 9907285. Bibcode: 1992PhRvA..45.2611M. https://link.aps.org/doi/10.1103/PhysRevA.45.2611.
- ↑ Eddi, A.; Fort, E.; Moisy, F.; Couder, Y. (16 June 2009). "Unpredictable Tunneling of a Classical Wave-Particle Association". Physical Review Letters 102 (24). doi:10.1103/PhysRevLett.102.240401. PMID 19658983. Bibcode: 2009PhRvL.102x0401E. http://stilton.tnw.utwente.nl/people/eddi/Papers/PhysRevLett_TUNNEL.pdf. Retrieved 1 May 2016.
- ↑ Bush, John W M; Oza, Anand U (2021-01-01). "Hydrodynamic quantum analogs". Reports on Progress in Physics 84 (1): 017001. doi:10.1088/1361-6633/abc22c. ISSN 0034-4885. PMID 33065567. https://iopscience.iop.org/article/10.1088/1361-6633/abc22c.
Further reading
- Binney, James; Skinner, David (2010). The physics of quantum mechanics (3. ed.). Great Malvern: Cappella Archive. ISBN 978-1-902918-51-8.
- Fröman, Nanny; Fröman, Per Olof (1965) (in en). JWKB Approximation: Contributions to the Theory. Amsterdam: North-Holland. ISBN 978-0-7204-0085-4.
- Griffiths, David J. (2004). Introduction to electrodynamics (3. ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 978-0-13-805326-0. https://archive.org/details/introductiontoel00grif_0.
- Liboff, Richard L. (2002). Introductory quantum mechanics (4th ed.). San Francisco: Addison-Wesley. ISBN 978-0-8053-8714-8.
- Muller-kirsten, Harald J. W. (2012) (in en). Introduction To Quantum Mechanics: Schrodinger Equation And Path Integral (2nd ed.). Singapore: World Scientific Publishing Company. ISBN 978-981-4397-76-6.
- Razavy, Mohsen (2003). Quantum theory of tunneling. River Edge, NJ: World Scientific. ISBN 978-981-238-019-7. OCLC ocm52498470. https://archive.org/details/quantumtheoryoft0000raza.
- Hong, Jooyoo; Vilenkin, Alexander; Winitzki, Serge (2003). "Particle creation in a tunneling universe." (in en). Physical Review D 68 (2). doi:10.1103/PhysRevD.68.023520. ISSN 0556-2821. Bibcode: 2003PhRvD..68b3520H.
- Wolf, E. L. (2012). Principles of electron tunneling spectroscopy. International series of monographs on physics (2nd ed.). Oxford; New York: Oxford University Press. ISBN 978-0-19-958949-4. OCLC 768067375.
External links
- Animation, applications and research linked to tunnel effect and other quantum phenomena (Université Paris Sud)
- Animated illustration of quantum tunnelling
- Animated illustration of quantum tunnelling in a RTD device
- Interactive Solution of Schrodinger Tunnel Equation
 |
