Physics:Lead–lead dating
Lead–lead dating is a method for dating geological samples, normally based on 'whole-rock' samples of material such as granite. For most dating requirements it has been superseded by uranium–lead dating (U–Pb dating), but in certain specialized situations (such as dating meteorites and the age of the Earth) it is more important than U–Pb dating.
Decay equations for common Pb–Pb dating
There are three stable "daughter" Pb isotopes that result from the radioactive decay of uranium and thorium in nature; they are 206Pb, 207Pb, and 208Pb. 204Pb is the only non-radiogenic lead isotope, therefore is not one of the daughter isotopes. These daughter isotopes are the final decay products of U and Th radioactive decay chains beginning from 238U, 235U and 232Th respectively. With the progress of time, the final decay product accumulates as the parent isotope decays at a constant rate. This shifts the ratio of radiogenic Pb versus non-radiogenic 204Pb (207Pb/204Pb or 206Pb/204Pb) in favor of radiogenic 207Pb or 206Pb. This can be expressed by the following decay equations:
- [math]\displaystyle{ {\left(\frac\ce{^{207}Pb}\ce{^{204}Pb}\right)_{P}} = {\left(\frac\ce{^{207}Pb}\ce{^{204}Pb}\right)_{I}} + {\left(\frac\ce{^{235}U}\ce{^{204}Pb}\right)_{P}} {\left({e^{\lambda_{235}t}-1}\right)} }[/math]
- [math]\displaystyle{ {\left(\frac\ce{^{206}Pb}\ce{^{204}Pb}\right)_{P}} = {\left(\frac\ce{^{206}Pb}\ce{^{204}Pb}\right)_{I}} + {\left(\frac\ce{^{238}U}\ce{^{204}Pb}\right)_{P}} {\left({e^{\lambda_{238}t}-1}\right)} }[/math]
where the subscripts P and I refer to present-day and initial Pb isotope ratios, λ235 and λ238 are decay constants for 235U and 238U, and t is the age.
The concept of common Pb–Pb dating (also referred to as whole rock lead isotope dating) was deduced through mathematical manipulation of the above equations.[1] It was established by dividing the first equation above by the second, under the assumption that the U/Pb system was undisturbed. This rearranged equation formed:
- [math]\displaystyle{ \left[\frac{\left(\frac\ce{^{207}Pb}\ce{^{204}Pb}\right)_{P}-\left(\frac\ce{^{207}Pb}\ce{^{204}Pb}\right)_{I}}{\left(\frac\ce{^{206}Pb}\ce{^{204}Pb}\right)_{P}-\left(\frac\ce{^{206}Pb}\ce{^{204}Pb}\right)_{I}}\right]= {\left(\frac{1}{137.88}\right)}{\left(\frac{e^{\lambda_{235}t}-1}{e^{\lambda_{238}t}-1}\right)} }[/math]
where the factor of 137.88 is the present-day 238U/235U ratio. As evident by the equation, initial Pb isotope ratios, as well as the age of the system are the two factors which determine the present day Pb isotope compositions. If the sample behaved as a closed system then graphing the difference between the present and initial ratios of 207Pb/204Pb versus 206Pb/204Pb should produce a straight line. The distance the point moves along this line is dependent on the U/Pb ratio, whereas the slope of the line depends on the time since Earth's formation. This was first established by Nier et al., 1941.[1]
The development of the Geochron database
The development of the Geochron database was mainly attributed to Clair Cameron Patterson’s application of Pb–Pb dating on meteorites in 1956. The Pb ratios of three stony and two iron meteorites were measured.[2] The dating of meteorites would then help Patterson in determining not only the age of these meteorites but also the age of Earth's formation. By dating meteorites Patterson was directly dating the age of various planetesimals. Assuming the process of elemental differentiation is identical on Earth as it is on other planets, the core of these planetesimals would be depleted of uranium and thorium, while the crust and mantle would contain higher U/Pb ratios. As planetesimals collided, various fragments were scattered and produced meteorites. Iron meteorites were identified as pieces of the core, while stony meteorites were segments of the mantle and crustal units of these various planetesimals.
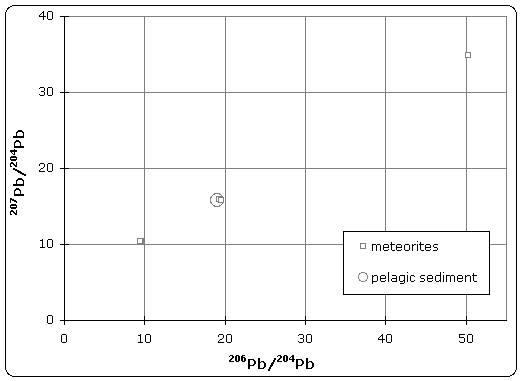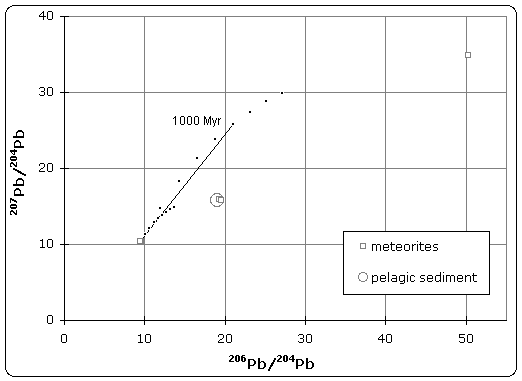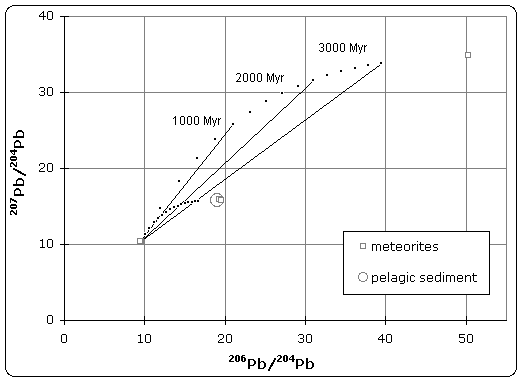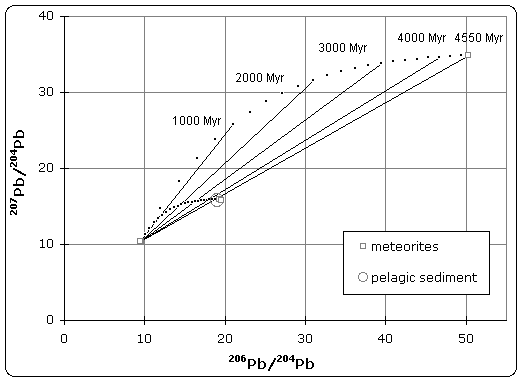
Samples of iron meteorite from Canyon Diablo (Meteor Crater) Arizona were found to have the least radiogenic composition of any material in the solar system. The U/Pb ratio was so low that no radiogenic decay was detected in the isotopic composition.[3] As illustrated in figure 1, this point defines the lower (left) end of the isochron. Therefore, troilite found in Canyon Diablo represents the primeval lead isotope composition of the solar system, dating back to 4.55 +/- 0.07 Byr.
Stony meteorites however, exhibited very high 207Pb/204Pb versus 206Pb/204Pb ratios, indicating that these samples came from the crust or mantle of the planetesimal. Together, these samples define an isochron, whose slope gives the age of meteorites as 4.55 Byr.
Patterson also analyzed terrestrial sediment collected from the ocean floor, which was believed to be representative of the Bulk Earth composition. Because the isotope composition of this sample plotted on the meteorite isochron, it suggested that earth had the same age and origin as meteorites, therefore solving the age of the Earth and giving rise to the name 'geochron'.
Lead isotope isochron diagram used by C. C. Patterson to determine the age of the Earth in 1956. Animation shows progressive growth over 4550 million years (Myr) of the lead isotope ratios for two stony meteorites (Nuevo Laredo and Forest City) from initial lead isotope ratios matching those of the Canyon Diablo iron meteorite.
Precise Pb–Pb dating of meteorites
Chondrules and calcium–aluminium-rich inclusions (CAIs) are spherical particles that make up chondritic meteorites and are believed to be the oldest objects in the Solar System. Hence precise dating of these objects is important to constrain the early evolution of the Solar System and the age of the Earth. The U–Pb dating method can yield the most precise ages for early Solar System objects due to the optimal half-life of 238U. However, the absence of zircon or other uranium-rich minerals in chondrites, and the presence of initial non-radiogenic Pb (common Pb), rules out direct use of the U-Pb concordia method. Therefore, the most precise dating method for these meteorites is the Pb–Pb method, which allows a correction for common Pb.[3]
When the abundance of 204Pb is relatively low, this isotope has larger measurement errors than the other Pb isotopes, leading to very strong correlation of errors between the measured ratios. This makes it difficult to determine the analytical uncertainty on the age. To avoid this problem, researchers[5] developed an 'alternative Pb–Pb isochron diagram' (see figure) with reduced error correlation between the measured ratios. In this diagram the 204Pb/206Pb ratio (the reciprocal of the normal ratio) is plotted on the x-axis, so that a point on the y axis (zero 204Pb/206Pb) would have infinitely radiogenic Pb. The ratio plotted on this axis is the 207Pb/206Pb ratio, corresponding to the slope of a normal Pb/Pb isochron, which yields the age. The most accurate ages are produced by samples near the y-axis, which was achieved by step-wise leaching and analysis of the samples.
Previously, when applying the alternative Pb–Pb isochron diagram, the 238U/235U isotope ratios were assumed to be invariant among meteoritic material. However, it has been shown that 238U/235U ratios are variable among meteoritic material.[6] To accommodate this, U-corrected Pb–Pb dating analysis is used to generate ages for the oldest solid material in the Solar System using a revised 238U/235U value of 137.786 ± 0.013 to represent the mean 238U/235U isotope ratio bulk inner Solar System materials.[4]
The result of U-corrected Pb–Pb dating has produced ages of 4567.35 ± 0.28 My for CAIs (A) and chondrules with ages between 4567.32 ± 0.42 and 4564.71 ± 0.30 My (B and C) (see figure). This supports the idea that CAIs crystallization and chondrule formation occurred around the same time during the formation of the solar system. However, chondrules continued to form for approximately 3 My after CAIs. Hence the best age for the original formation of the Solar System is 4567.7 My. This date also represents the time of initiation of planetary accretion. Successive collisions between accreted bodies led to the formation of larger and larger planetesimals, finally forming the Earth–Moon system in a giant impact event.
The age difference between CAIs and chondrules measured in these studies verifies the chronology of the early Solar System derived from extinct short-lived nuclide methods such as 26Al-26Mg, thus improving our understanding of the development of the Solar System and the formation of the Earth.
References
- ↑ 1.0 1.1 Nier, Alfred O.; Thompson, Robert W.; Murphey, Byron F. (1941). "The Isotopic Constitution of Lead and the Measurement of Geological Time. III". Physical Review 60 (2): 112–116. doi:10.1103/PhysRev.60.112. Bibcode: 1941PhRv...60..112N.
- ↑ Patterson, Claire (1956). "Age of meteorites and the earth". Geochimica et Cosmochimica Acta 10 (4): 230–237. doi:10.1016/0016-7037(56)90036-9. Bibcode: 1956GeCoA..10..230P.
- ↑ 3.0 3.1 Dickin, Alan P. (2005). Radiogenic Isotope Geology. p. 117. doi:10.1017/CBO9781139165150. ISBN 9781139165150.
- ↑ 4.0 4.1 Connelly, J. N.; Bizzarro, M.; Krot, A. N.; Nordlund, A.; Wielandt, D.; Ivanova, M. A. (2012). "The Absolute Chronology and Thermal Processing of Solids in the Solar Protoplanetary Disk". Science 338 (6107): 651–655. doi:10.1126/science.1226919. PMID 23118187. Bibcode: 2012Sci...338..651C.
- ↑ Amelin, Y.; Krot, Alexander N.; Hutcheon, Ian D.; Ulyanov, Alexander A. (2002). "Lead Isotopic Ages of Chondrules and Calcium-Aluminum-Rich Inclusions". Science 297 (5587): 1678–1683. doi:10.1126/science.1073950. PMID 12215641. Bibcode: 2002Sci...297.1678A.
- ↑ Brennecka, G. A.; Weyer, S.; Wadhwa, M.; Janney, P. E.; Zipfel, J.; Anbar, A. D. (2010). "238U/235U Variations in Meteorites: Extant 247Cm and Implications for Pb-Pb Dating". Science 327 (5964): 449–451. doi:10.1126/science.1180871. PMID 20044543. Bibcode: 2010Sci...327..449B.
External links
 |