Physics:Lenticular lens

A series of cylindrical lenses molded in a plastic substrate

A lenticular lens is an array of lenses, designed so that when viewed from slightly different angles, different parts of the image underneath are shown. The most common example is the lenses used in lenticular printing, where the technology is used to give an illusion of depth, or to make images that appear to change or move as the image is viewed from different angles.

Applications

Lenticular printing

Principle of operation of an animated or 3D lenticular print, showing repetition of views

Lenticular printing is a multi-step process consisting of creating a lenticular image from at least two existing images, and combining it with a lenticular lens. This process can be used to create various frames of animation (for a motion effect), offsetting the various layers at different increments (for a 3D effect), or simply to show a set of alternate images which may appear to transform into each other.

Corrective lenses

Lenticular lenses are sometimes used as corrective lenses for improving vision. A bifocal lens could be considered a simple example.

Lenticular eyeglass lenses have been employed to correct extreme hyperopia (farsightedness), a condition often created by cataract surgery when lens implants are not possible. To limit the great thickness and weight that such high-power lenses would otherwise require, all the power of the lens is concentrated in a small area in the center. In appearance, such a lens is often described as resembling a fried egg: a hemisphere atop a flat surface. The flat surface or "carrier lens" has little or no power and is there merely to fill up the rest of the eyeglass frame and to hold or "carry" the lenticular portion of the lens. This portion is typically 40 mm (1.6 in) in diameter but may be smaller, as little as 20 mm (0.79 in), in sufficiently high powers. These lenses are generally used for plus (hyperopic) corrections at about 12 diopters or higher. A similar sort of eyeglass lens is the myodisc, sometimes termed a minus lenticular lens, used for very high negative (myopic) corrections. More aesthetic aspheric lens designs are sometimes fitted. A film made of cylindrical lenses molded in a plastic substrate as shown in above picture, can be applied to the inside of standard glasses to correct for diplopia. The film is typically applied to the eye with the good muscle control of direction. Diplopia (also known as double vision) is typically caused by a sixth cranial nerve palsy that prevents full control of the muscles that control the direction the eye is pointed in. These films are defined in the number of degrees of correction that is needed where the higher the degree, the higher the directive correction that is needed.

Lenticular screens

Screens with a molded lenticular surface are frequently used with projection television systems. In this case, the purpose of the lenses is to focus more of the light into a horizontal beam and allow less of the light to escape above and below the plane of the viewer. In this way, the apparent brightness of the image is increased.

Ordinary front-projection screens can also be described as lenticular. In this case, rather than transparent lenses, the shapes formed are tiny curved reflectors. Lenticular screens are most often used for ambient light rejecting projector screens for ultra-short throw projectors. The lenticular structure of the surface reflects the light from the projector to the viewer without reflecting the light from sources above the screen.

3D television

(As of 2010), a number of manufacturers were developing auto-stereoscopic high definition 3D televisions, using lenticular lens systems to avoid the need for special spectacles. One of these, Chinese manufacturer TCL, was selling a 42-inch (110 cm) LCD model—the TD-42F—in China for around US$20,000.

In 2021 only specialist manufacturers are making these kinds of display.

Lenticular color motion picture processes

Lenticular lenses were used in early color motion picture processes of the 1920s such as the Keller-Dorian system and Kodacolor. This enabled color pictures with the use of merely monochrome film stock.

Angle of view of a lenticular print

The angle of view of a lenticular print is the range of angles within which the observer can see the entire image. This is determined by the maximum angle at which a ray can leave the image through the correct lenticule.

Angle within the lens

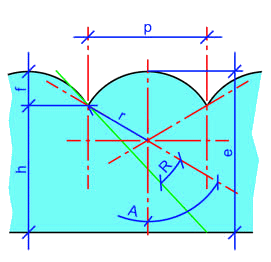
The diagram at right shows in green the most extreme ray within the lenticular lens that will be refracted correctly by the lens. This ray leaves one edge of an image strip (at the lower right) and exits through the opposite edge of the corresponding lenticule.

Definitions

• [math]\displaystyle{ R }[/math] is the angle between the extreme ray and the normal at the point where it exits the lens,
• [math]\displaystyle{ p }[/math] is the pitch, or width of each lenticular cell,
• [math]\displaystyle{ r }[/math] is the radius of curvature of the lenticule,
• [math]\displaystyle{ e }[/math] is the thickness of the lenticular lens
• [math]\displaystyle{ h }[/math] is the thickness of the substrate below the curved surface of the lens, and
• [math]\displaystyle{ n }[/math] is the lens's index of refraction.

Calculation

[math]\displaystyle{ R=A-\arctan\left({p \over h}\right) }[/math],

where

[math]\displaystyle{ A=\arcsin \left({p \over 2r}\right) }[/math],

[math]\displaystyle{ h=e-f }[/math] is the distance from the back of the grating to the edge of the lenticule, and

[math]\displaystyle{ f=r-\sqrt{r^2-\left({p \over 2}\right)^2} }[/math].

Angle outside the lens

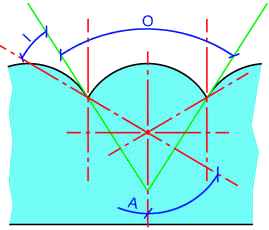
The angle outside the lens is given by refraction of the ray determined above. The full angle of observation [math]\displaystyle{ O }[/math] is given by

[math]\displaystyle{ O=2(A-I) }[/math],

where [math]\displaystyle{ I }[/math] is the angle between the extreme ray and the normal outside the lens. From Snell's Law,

[math]\displaystyle{ I=\arcsin \left({n\sin(R) \over n_a}\right) }[/math],

where [math]\displaystyle{ n_a \approx 1.0003 }[/math] is the index of refraction of air.

Example

Consider a lenticular print that has lenses with 336.65 µm pitch, 190.5 µm radius of curvature, 457 µm thickness, and an index of refraction of 1.557. The full angle of observation [math]\displaystyle{ O }[/math] would be 64.6°.

Rear focal plane of a lenticular network

The focal length of the lens is calculated from the lensmaker's equation, which in this case simplifies to:

[math]\displaystyle{ F={r \over n-1} }[/math],

where [math]\displaystyle{ F }[/math] is the focal length of the lens.

The back focal plane is located at a distance [math]\displaystyle{ BFD }[/math] from the back of the lens:

[math]\displaystyle{ BFD=F- {e \over n}. }[/math]

A negative BFD indicates that the focal plane lies inside the lens.

In most cases, lenticular lenses are designed to have the rear focal plane coincide with the back plane of the lens. The condition for this coincidence is [math]\displaystyle{ BFD=0 }[/math], or

[math]\displaystyle{ e={nr \over n-1}. }[/math]

This equation imposes a relation between the lens thickness [math]\displaystyle{ e }[/math] and its radius of curvature [math]\displaystyle{ r }[/math].

Example

The lenticular lens in the example above has focal length 342 µm and back focal distance 48 µm, indicating that the focal plane of the lens falls 48 micrometers behind the image printed on the back of the lens.

See also

• Fresnel lens, a different 'flat' lens technology
• Integral imaging
• Microlens

References

• Bartholdi, Paul (1997). "Quelques notions d'optique" (in fr). Observatoire de Genève. http://obswww.unige.ch/~bartho/Optic/Optic/node1.html. 
• Soulier, Bernard (2002). "Principe de fonctionnement de l'optique lenticulaire" (in fr). Séquence 3d. http://sq3d.v2.free.fr/fr_pages/technique/optique_0.html. 
• Okoshi, Takanori Three-Dimensional Imaging Techniques Atara Press (2011), ISBN:978-0-9822251-4-1.

External links

• Lecture slides covering lenticular lenses (PowerPoint) by John Canny
• Choosing the right lenticular sheet for inkjet printer
• http://www.microlens.com/pdfs/history_of_lenticular.pdf