Physics:Macroscopic quantum phenomena
Macroscopic quantum phenomena are processes showing quantum behaviour at the macroscopic scale, rather than at the atomic scale where quantum effects are prevalent. The best-known examples of macroscopic quantum phenomena are superfluidity and superconductivity; other examples include the quantum Hall effect, Josephson effect and topological order. Since 2000 there has been extensive experimental work on quantum gases, particularly Bose–Einstein condensates.
As of 2025, seven Nobel Prizes in Physics have been awarded for work related to macroscopic quantum phenomena.[lower-alpha 1] Macroscopic quantum phenomena can be observed in superfluid helium and in superconductors,[1] but also in dilute quantum gases, dressed photons such as polaritons and in laser light. Although these media are very different, they are all similar in that they show macroscopic quantum behaviour, and in this respect they all can be referred to as quantum fluids.
Quantum phenomena are generally classified as macroscopic when the quantum states are occupied by a large number of particles (of the order of the Avogadro number) or the quantum states involved are macroscopic in size (up to kilometre-sized in superconducting wires).[2]
Consequences of the macroscopic occupation
The concept of macroscopically occupied quantum states is introduced by Fritz London.[3][4] In this section it will be explained what it means if a single state is occupied by a very large number of particles. We start with the wave function of the state written as
|
|
( ) |
with Ψ0 the amplitude and the phase. The wave function is normalized so that
|
|
( ) |
The physical interpretation of the quantity
|
|
() |
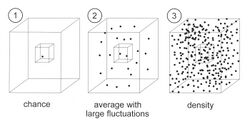
depends on the number of particles. Fig. 1 represents a container with a certain number of particles with a small control volume ΔV inside. We check from time to time how many particles are in the control box. We distinguish three cases:
- There is only one particle. In this case the control volume is empty most of the time. However, there is a certain chance to find the particle in it given by Eq. (3). The probability is proportional to ΔV. The factor ΨΨ∗ is called the chance density.
- If the number of particles is a bit larger there are usually some particles inside the box. We can define an average, but the actual number of particles in the box has relatively large fluctuations around this average.
- In the case of a very large number of particles there will always be a lot of particles in the small box. The number will fluctuate but the fluctuations around the average are relatively small. The average number is proportional to ΔV and ΨΨ∗ is now interpreted as the particle density.
In quantum mechanics the particle probability flow density Jp (unit: particles per second per m2), also called probability current, can be derived from the Schrödinger equation to be
|
|
( ) |
with q the charge of the particle and the vector potential; cc stands for the complex conjugate of the other term inside the brackets.[5] For neutral particles q = 0, for superconductors q = −2e (with e the elementary charge) the charge of Cooper pairs. With Eq. (1)
|
|
( ) |
If the wave function is macroscopically occupied the particle probability flow density becomes a particle flow density. We introduce the fluid velocity vs via the mass flow density
|
|
( ) |
The density (mass per volume) is
|
|
( ) |
so Eq. (5) results in
|
|
( ) |
This important relation connects the velocity, a classical concept, of the condensate with the phase of the wave function, a quantum-mechanical concept.
Superfluidity

At temperatures below the lambda point, helium shows the unique property of superfluidity. The fraction of the liquid that forms the superfluid component is a macroscopic quantum fluid. The helium atom is a neutral particle, so q = 0. Furthermore, when considering helium-4, the relevant particle mass is m = m4, so Eq. (8) reduces to
|
|
( ) |
For an arbitrary loop in the liquid, this gives
|
|
( ) |
Due to the single-valued nature of the wave function
|
|
() |
with n integer, we have
|
|
() |
The quantity
|
|
( ) |
is the quantum of circulation. For a circular motion with radius r
|
|
( ) |
In case of a single quantum (n = 1)
|
|
( ) |
When superfluid helium is put in rotation, Eq. (13) will not be satisfied for all loops inside the liquid unless the rotation is organized around vortex lines (as depicted in Fig. 2). These lines have a vacuum core with a diameter of about 1 Å (which is smaller than the average particle distance). The superfluid helium rotates around the core with very high speeds. Just outside the core (r = 1 Å), the velocity is as large as 160 m/s. The cores of the vortex lines and the container rotate as a solid body around the rotation axes with the same angular velocity. The number of vortex lines increases with the angular velocity (as shown in the upper half of the figure). Note that the two right figures both contain six vortex lines, but the lines are organized in different stable patterns.[6]
Superconductivity
In the original paper[7] Ginzburg and Landau observed the existence of two types of superconductors depending on the energy of the interface between the normal and superconducting states. The Meissner state breaks down when the applied magnetic field is too large. Superconductors can be divided into two classes according to how this breakdown occurs. In Type I superconductors, superconductivity is abruptly destroyed when the strength of the applied field rises above a critical value Hc. Depending on the geometry of the sample, one may obtain an intermediate state[8] consisting of a baroque pattern of regions of normal material carrying a magnetic field mixed with regions of superconducting material containing no field. In Type II superconductors, raising the applied field past a critical value Hc1 leads to a mixed state (also known as the vortex state) in which an increasing amount of magnetic flux penetrates the material, but there remains no resistance to the flow of electric current as long as the current is not too large. At a second critical field strength Hc2, superconductivity is destroyed. The mixed state is actually caused by vortices in the electronic superfluid, sometimes called fluxons because the flux carried by these vortices is quantized. Most pure elemental superconductors, except niobium and carbon nanotubes, are Type I, while almost all impure and compound superconductors are Type II.
The most important finding from Ginzburg–Landau theory was made by Alexei Abrikosov in 1957. He used Ginzburg–Landau theory to explain experiments on superconducting alloys and thin films. He found that in a type-II superconductor in a high magnetic field, the field penetrates in a triangular lattice of quantized tubes of flux vortices. For this and related work, he was awarded the Nobel Prize in 2003 with Ginzburg and Leggett.[9]
Fluxoid quantization
For superconductors the bosons involved are the so-called Cooper pairs which are quasiparticles formed by two electrons.[10] Hence m = 2me and q = −2e where me and e are the mass of an electron and the elementary charge. It follows from Eq. (8) that
|
|
( ) |
Integrating Eq. (15) over a closed loop gives
|
|
( ) |
As in the case of helium we define the vortex strength
|
|
( ) |
and use the general relation
|
|
( ) |
where Φ is the magnetic flux enclosed by the loop. The so-called fluxoid is defined by
|
|
( ) |
In general the values of κ and Φ depend on the choice of the loop. Due to the single-valued nature of the wave function and Eq. (16) the fluxoid is quantized
|
|
( ) |
The unit of quantization is called the flux quantum
|
|
( ) |
The flux quantum plays a very important role in superconductivity. The earth magnetic field is very small (about 50 μT), but it generates one flux quantum in an area of 6 μm by 6 μm. So, the flux quantum is very small. Yet it was measured to an accuracy of 9 digits as shown in Eq. (21). Nowadays the value given by Eq. (21) is exact by definition.

- thick superconducting ring. The integration loop is completely in the region with vs = 0;
- thick superconducting ring with a weak link. The integration loop is completely in the region with vs = 0 except for a small region near the weak link.
In Fig. 3 two situations are depicted of superconducting rings in an external magnetic field. One case is a thick-walled ring and in the other case the ring is also thick-walled, but is interrupted by a weak link. In the latter case we will meet the famous Josephson relations. In both cases we consider a loop inside the material. In general a superconducting circulation current will flow in the material. The total magnetic flux in the loop is the sum of the applied flux Φa and the self-induced flux Φs induced by the circulation current
|
|
( ) |
Thick ring
The first case is a thick ring in an external magnetic field (Fig. 3a). The currents in a superconductor only flow in a thin layer at the surface. The thickness of this layer is determined by the so-called London penetration depth. It is of μm size or less. We consider a loop far away from the surface so that vs = 0 everywhere so κ = 0. In that case the fluxoid is equal to the magnetic flux (Φv = Φ). If vs = 0 Eq. (15) reduces to
|
|
( ) |
Taking the rotation gives
|
|
( ) |
Using the well-known relations and shows that the magnetic field in the bulk of the superconductor is zero as well. So, for thick rings, the total magnetic flux in the loop is quantized according to
|
|
( ) |
Interrupted ring, weak link s

Weak links play a very important role in modern superconductivity. In most cases weak links are oxide barriers between two superconducting thin films, but it can also be a crystal boundary (in the case of high-Tc superconductors). A schematic representation is given in Fig. 4. Now consider the ring which is thick everywhere except for a small section where the ring is closed via a weak link (Fig. 3b). The velocity is zero except near the weak link. In these regions the velocity contribution to the total phase change in the loop is given by (with Eq. (15))
|
|
( ) |
The line integral is over the contact from one side to the other in such a way that the end points of the line are well inside the bulk of the superconductor where vs = 0. So the value of the line integral is well-defined (e.g. independent of the choice of the end points). With Eqs. (19), (22), and (26)
|
|
( ) |
Without proof we state that the supercurrent through the weak link is given by the so-called DC Josephson relation[11]
|
|
( ) |
The voltage over the contact is given by the AC Josephson relation
|
|
( ) |
The names of these relations (DC and AC relations) are misleading since they both hold in DC and AC situations. In the steady state (constant ) Eq. (29) shows that V=0 while a nonzero current flows through the junction. In the case of a constant applied voltage (voltage bias) Eq. (29) can be integrated easily and gives
|
|
( ) |
Substitution in Eq. (28) gives
|
|
( ) |
This is an AC current. The frequency
|
|
( ) |
is called the Josephson frequency. One μV gives a frequency of about 500 MHz. By using Eq. (32) the flux quantum is determined with the high precision as given in Eq. (21).
The energy difference of a Cooper pair, moving from one side of the contact to the other, is ΔE = 2eV. With this expression Eq. (32) can be written as ΔE = hν which is the relation for the energy of a photon with frequency ν.
- The AC Josephson relation (Eq. (29)) can be easily understood in terms of Newton's law, (or from one of the London equation's[12]). We start with Newton's law
- Substituting the expression for the Lorentz force and using the general expression for the co-moving time derivative gives
- Eq. (8) gives so
- Take the line integral of this expression. In the end points the velocities are zero so the ∇v2 term gives no contribution. Using and Eq. (26), with q = −2e and m = 2me, gives Eq. (29).
DC SQUID


Fig. 5 shows a so-called DC SQUID. It consists of two superconductors connected by two weak links. The fluxoid quantization of a loop through the two bulk superconductors and the two weak links demands
|
|
( ) |
If the self-inductance of the loop can be neglected the magnetic flux in the loop Φ is equal to the applied flux
|
|
( ) |
with B the magnetic field, applied perpendicular to the surface, and A the surface area of the loop. The total supercurrent is given by
|
|
( ) |
Substitution of Eq(33) in (35) gives
|
|
( ) |
Using a well known geometrical formula we get
|
|
( ) |
Since the sin-function can vary only between −1 and +1 a steady solution is only possible if the applied current is below a critical current given by
|
|
( ) |
Note that the critical current is periodic in the applied flux with period Φ0. The dependence of the critical current on the applied flux is depicted in Fig. 6. It has a strong resemblance with the interference pattern generated by a laser beam behind a double slit. In practice the critical current is not zero at half integer values of the flux quantum of the applied flux. This is due to the fact that the self-inductance of the loop cannot be neglected.[13]
Type II superconductivity
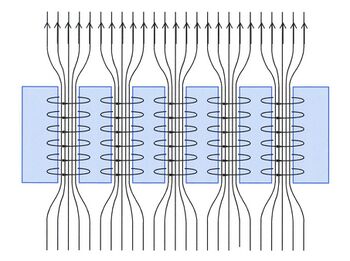
Type-II superconductivity is characterized by two critical fields called Bc1 and Bc2. At a magnetic field Bc1 the applied magnetic field starts to penetrate the sample, but the sample is still superconducting. Only at a field of Bc2 the sample is completely normal. For fields in between Bc1 and Bc2 magnetic flux penetrates the superconductor in well-organized patterns, the so-called Abrikosov vortex lattice similar to the pattern shown in Fig. 2.[14] A cross section of the superconducting plate is given in Fig. 7. Far away from the plate the field is homogeneous, but in the material superconducting currents flow which squeeze the field in bundles of exactly one flux quantum. The typical field in the core is as big as 1 tesla. The currents around the vortex core flow in a layer of about 50 nm with current densities on the order of 15×1012 A/m2. That corresponds with 15 million ampère in a wire of one mm2.
Dilute quantum gases
The classical types of quantum systems, superconductors and superfluid helium, were discovered in the beginning of the 20th century. Near the end of the 20th century, scientists discovered how to create very dilute atomic or molecular gases, cooled first by laser cooling and then by evaporative cooling.[15] They are trapped using magnetic fields or optical dipole potentials in ultrahigh vacuum chambers. Isotopes which have been used include rubidium (Rb-87 and Rb-85), strontium (Sr-87, Sr-86, and Sr-84) potassium (K-39 and K-40), sodium (Na-23), lithium (Li-7 and Li-6), and hydrogen (H-1). The temperatures to which they can be cooled are as low as a few nanokelvin. The developments have been very fast in the past few years. A team of NIST and the University of Colorado has succeeded in creating and observing vortex quantization in these systems.[16] The concentration of vortices increases with the angular velocity of the rotation, similar to the case of superfluid helium and superconductivity.
Mechanical systems
Macroscopic quantum effects have been observed in the motion of engineered mechanical objects.[17] Research in the field of quantum optomechanics focuses on the manipulation of the quantized vibrational states (phonons) of mechanical resonators.[18]
Control is realized via two primary experimental architectures. Cavity optomechanics uses laser light in an optical cavity to couple to the motion of objects like mirrors or membranes.[19] Circuit electromechanics uses superconducting microwave circuits to couple to piezoelectric resonators, typically realized as surface acoustic wave (SAW) or bulk acoustic resonator (BAR) devices.[20] Both architectures have been used to cool massive resonators to their quantum ground state.[21][22]
A landmark experiment in 2010, using an electromechanical system, was the first to demonstrate the deterministic preparation of non-classical states in a mechanical resonator.[21] This work achieved cooling to the quantum ground state (), preparation of a single-phonon Fock state (), and the generation of a quantum superposition between these two states (). This achievement was recognized by Science as its 2010 Breakthrough of the Year.[23]
Progress in both architectures has also enabled the demonstration of quantum entanglement between two distinct macroscopic mechanical resonators.[24][25]
See also
- Charge density wave
- Chiral magnetic effect
- Domain wall (magnetism)
- Flux pinning
- Ginzburg–Landau theory
- Husimi Q representation
- Josephson effect
- Magnetic flux quantum
- Meissner effect
- N-slit interferometric equation
- Quantum boomerang effect
- Quantum machine
- Quantum turbulence
- Quantum vortex
- Schrödinger's cat paradox
- Second sound
- SQUID
- Superconductivity
- Topological defect
- Type-I superconductor
- Type-II superconductor
Notes
- ↑ These Nobel prizes were:
- 1996 - for the discovery of superfluidity in helium-3;
- 1998 - for the discovery of the fractional quantum Hall effect;
- 2001 - for the demonstration of Bose–Einstein condensation;
- 2003 - for contributions to the theory of superconductivity and superfluidity;
- 2007 - for the discovery of giant magnetoresistance (2007);
- 2016 - for theoretical discoveries of topological phase transitions and topological phases of matter;
- 2025 - macroscopic phenomena in Josephson junctions (see phase qubit).
References and footnotes
- ↑ D.R. Tilley and J. Tilley, Superfluidity and Superconductivity, Adam Hilger, Bristol and New York, 1990
- ↑ Jaeger, Gregg (September 2014). "What in the (quantum) world is macroscopic?". American Journal of Physics 82 (9): 896–905. doi:10.1119/1.4878358. Bibcode: 2014AmJPh..82..896J.
- ↑ Fritz London Superfluids (London, Wiley, 1954–1964)
- ↑ Gavroglu, K.; Goudaroulis, Y. (1988). "Understanding macroscopic quantum phenomena: The history of superfluidity 1941–1955". Annals of Science 45 (4): 367. doi:10.1080/00033798800200291.
- ↑ "The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity, Section 21-5: Superconductivity". https://feynmanlectures.caltech.edu/III_21.html.
- ↑ E.J. Yarmchuk; R.E. Packard (1982). "Photographic studies of quantized vortex lines". J. Low Temp. Phys. 46 (5–6): 479. doi:10.1007/BF00683912. Bibcode: 1982JLTP...46..479Y.
- ↑ Landau, Lev Davidovich; Ginzburg, Vitaly L (1950). "On the theory of superconductivity" (in en). Zh. Eksp. Teor. Fiz. 20. https://cds.cern.ch/record/486430.
- ↑ Lev D. Landau; Evgeny M. Lifschitz (1984). Electrodynamics of Continuous Media. Course of Theoretical Physics. 8. Oxford: Butterworth-Heinemann. ISBN 978-0-7506-2634-7.
- ↑ Abrikosov, Alexei A. (2004-07-19). "Type H Superconductors and the Vortex Lattice" (in en). ChemPhysChem 5 (7): 924–929. doi:10.1002/cphc.200400138. ISSN 1439-4235. PMID 15298378.
- ↑ M. Tinkham (1975). Introduction to Superconductivity. McGraw-Hill.
- ↑ B.D. Josephson (1962). "Possible new effects in superconductive tunneling". Phys. Lett. 1 (7): 251–253. doi:10.1016/0031-9163(62)91369-0. Bibcode: 1962PhL.....1..251J.
- ↑ London, F.; London, H. (1935). "The Electromagnetic Equations of the Supraconductor". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 149 (866): 71. doi:10.1098/rspa.1935.0048. Bibcode: 1935RSPSA.149...71L.
- ↑ A.TH.A.M. de Waele; R. de Bruyn Ouboter (1969). "Quantum-interference phenomena in point contacts between two superconductors". Physica 41 (2): 225–254. doi:10.1016/0031-8914(69)90116-5. Bibcode: 1969Phy....41..225D.
- ↑ Essmann, U.; Träuble, H. (1967). "The direct observation of individual flux lines in type II superconductors". Physics Letters A 24 (10): 526. doi:10.1016/0375-9601(67)90819-5. Bibcode: 1967PhLA...24..526E.
- ↑ Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. (1995). "Observation of Bose–Einstein Condensation in a Dilute Atomic Vapor". Science 269 (5221): 198–201. doi:10.1126/science.269.5221.198. PMID 17789847. Bibcode: 1995Sci...269..198A.
- ↑ Schweikhard, V.; Coddington, I.; Engels, P.; Tung, S.; Cornell, E.A. (2004). "Vortex-Lattice Dynamics in Rotating Spinor Bose-Einstein Condensates". Phys. Rev. Lett. 93 (3): 210403. doi:10.1103/PhysRevLett.93.030403. PMID 15323808. Bibcode: 2004PhRvL..93c0403N.
- ↑ Aspelmeyer, Markus; Kippenberg, Tobias J.; Marquardt, Florian (2014). "Cavity optomechanics". Reviews of Modern Physics 86 (4): 1391–1452. doi:10.1103/RevModPhys.86.1391. Bibcode: 2014RvMP...86.1391A.
- ↑ Barzanjeh, Shabir; Xuereb, André; Gröblacher, Simon; Paternostro, Mauro; Regal, Cindy A.; Weig, Eva M. (2022). "Optomechanics for quantum technologies". Nature Physics 18 (1): 15–24. doi:10.1038/s41567-021-01402-0. Bibcode: 2022NatPh..18...15B.
- ↑ Aspelmeyer, Markus; Kippenberg, Tobias J.; Marquardt, Florian (2014). "Cavity optomechanics". Reviews of Modern Physics 86 (4): 1391–1452. doi:10.1103/RevModPhys.86.1391. Bibcode: 2014RvMP...86.1391A.
- ↑ Clerk, A. A.; Lehnert, K. W.; Bertet, P.; Nakamura, Y.; Schoelkopf, R. J. (2020). "Hybrid quantum systems with circuit quantum electrodynamics". Nature Physics 16 (3): 257–267. doi:10.1038/s41567-020-0797-9. Bibcode: 2020NatPh..16..257C.
- ↑ 21.0 21.1 O’Connell, A. D.; Hofheinz, M.; Ansmann, M.; Bialczak, R. C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D. et al. (2010). "Quantum ground state and single-phonon control of a mechanical resonator". Nature 464 (7289): 697–703. doi:10.1038/nature08967. PMID 20237473. Bibcode: 2010Natur.464..697O.
- ↑ Chan, Jasper; Alegre, Thiago P. Mayer; Safavi-Naeini, Amir H.; Hill, Jeff T.; Krause, Alex; Gröblacher, Simon; Aspelmeyer, Markus; Painter, Oskar (2011). "Laser cooling of a nanomechanical oscillator into its quantum ground state". Nature 478 (7367): 89–92. doi:10.1038/nature10461. PMID 21979049. Bibcode: 2011Natur.478...89C.
- ↑ Cho, Adrian (2010). "Breakthrough of the Year: The First Quantum Machine". Science 330 (6011): 1604. doi:10.1126/science.330.6011.1604. PMID 21163973.
- ↑ Kotler, Shlomi; Peterson, Gabriel A.; Shojaee, Ezad; Lecocq, Florent; Cicak, Katarina; Kwiatkowski, Alex; Geller, Shawn; Glancy, Scott et al. (7 May 2021). "Direct observation of deterministic macroscopic entanglement". Science 372 (6542): 622–625. doi:10.1126/science.abf2998. PMID 33958475. Bibcode: 2021Sci...372..622K.
- ↑ Mercier de Lépinay, Laure; Ockeloen-Korppi, Caspar F.; Woolley, Matthew J.; Oksanen, Mika; Sillanpää, Mika A. (7 May 2021). "Quantum mechanics-free subsystem with mechanical oscillators". Science 372 (6542): 625–629. doi:10.1126/science.abf5389. PMID 33958476. Bibcode: 2021Sci...372..625M.
 |
