Physics:Magnetostriction

From HandWiki
Short description: Property of materials that causes them to change their shape during magnetization

Magnetostriction is a property of magnetic materials that causes them to change their shape or dimensions during the process of magnetization. The variation of materials' magnetization due to the applied magnetic field changes the magnetostrictive strain until reaching its saturation value, λ. The effect was first identified in 1842 by James Joule when observing a sample of iron.[1]

Magnetostriction applies to magnetic fields, while electrostriction applies to electric fields.

Magnetostriction causes energy loss due to frictional heating in susceptible ferromagnetic cores, and is also responsible for the low-pitched humming sound that can be heard coming from transformers, where alternating currents produce a changing magnetic field.[2]

Explanation

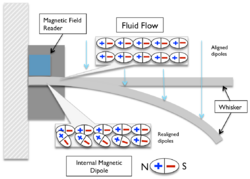
Internally, ferromagnetic materials have a structure that is divided into domains, each of which is a region of uniform magnetization. When a magnetic field is applied, the boundaries between the domains shift and the domains rotate; both of these effects cause a change in the material's dimensions. The reason that a change in the magnetic domains of a material results in a change in the material's dimensions is a consequence of magnetocrystalline anisotropy; it takes more energy to magnetize a crystalline material in one direction than in another. If a magnetic field is applied to the material at an angle to an easy axis of magnetization, the material will tend to rearrange its structure so that an easy axis is aligned with the field to minimize the free energy of the system. Since different crystal directions are associated with different lengths, this effect induces a strain in the material.[3]

The reciprocal effect, the change of the magnetic susceptibility (response to an applied field) of a material when subjected to a mechanical stress, is called the Villari effect. Two other effects are related to magnetostriction: the Matteucci effect is the creation of a helical anisotropy of the susceptibility of a magnetostrictive material when subjected to a torque and the Wiedemann effect is the twisting of these materials when a helical magnetic field is applied to them.

The Villari reversal is the change in sign of the magnetostriction of iron from positive to negative when exposed to magnetic fields of approximately 40 kA/m.

On magnetization, a magnetic material undergoes changes in volume which are small: of the order 10−6.

Magnetostrictive hysteresis loop

Magnetostrictive hysteresis loop of Mn-Zn ferrite for power applications measured by semiconductor strain gauges

Like flux density, the magnetostriction also exhibits hysteresis versus the strength of the magnetizing field. The shape of this hysteresis loop (called "dragonfly loop") can be reproduced using the Jiles-Atherton model.[4]

Magnetostrictive materials

Cut-away of a transducer comprising: magnetostrictive material (inside), magnetising coil, and magnetic enclosure completing the magnetic circuit (outside)

Magnetostrictive materials can convert magnetic energy into kinetic energy, or the reverse, and are used to build actuators and sensors. The property can be quantified by the magnetostrictive coefficient, λ, which may be positive or negative and is defined as the fractional change in length as the magnetization of the material increases from zero to the saturation value. The effect is responsible for the familiar "electric hum" (About this soundListen (help·info)) which can be heard near transformers and high power electrical devices.

Cobalt exhibits the largest room-temperature magnetostriction of a pure element at 60 microstrains. Among alloys, the highest known magnetostriction is exhibited by Terfenol-D, (Ter for terbium, Fe for iron, NOL for Naval Ordnance Laboratory, and D for dysprosium). Terfenol-D, Tb
xDy
1-xFe
2, exhibits about 2,000 microstrains in a field of 160 kA/m (2 kOe) at room temperature and is the most commonly used engineering magnetostrictive material.[5] Galfenol, Fe
xGa
1-x, and Alfer, Fe
xAl
1-x, are newer alloys that exhibit 200-400 microstrains at lower applied fields (~200 Oe) and have enhanced mechanical properties from the brittle Terfenol-D. Both of these alloys have <100> easy axes for magnetostriction and demonstrate sufficient ductility for sensor and actuator applications.[6]

Schematic of a whisker flow sensor developed using thin-sheet magnetostrictive alloys.

Another very common magnetostrictive composite is the amorphous alloy Fe
81Si
3.5B
13.5C
2 with its trade name Metglas 2605SC. Favourable properties of this material are its high saturation-magnetostriction constant, λ, of about 20 microstrains and more, coupled with a low magnetic-anisotropy field strength, HA, of less than 1 kA/m (to reach magnetic saturation). Metglas 2605SC also exhibits a very strong ΔE-effect with reductions in the effective Young's modulus up to about 80% in bulk. This helps build energy-efficient magnetic MEMS.[citation needed]

Cobalt ferrite, CoFe
2O
4 (CoO·Fe2O3), is also mainly used for its magnetostrictive applications like sensors and actuators, thanks to its high saturation magnetostriction (~200 parts per million).[7] In the absence of rare-earth elements, it is a good substitute for Terfenol-D.[8] Moreover, its magnetostrictive properties can be tuned by inducing a magnetic uniaxial anisotropy.[9] This can be done by magnetic annealing,[10] magnetic field assisted compaction,[11] or reaction under uniaxial pressure.[12] This last solution has the advantage of being ultrafast (20 min), thanks to the use of spark plasma sintering.

In early sonar transducers during World War II, nickel was used as a magnetostrictive material. To alleviate the shortage of nickel, the Japanese navy used an iron-aluminium alloy from the Alperm family.

Mechanical behaviors of magnetostrictive alloys

Effect of microstructure on elastic strain alloys

Single-crystal alloys exhibit superior microstrain, but are vulnerable to yielding due to the anisotropic mechanical properties of most metals. It has been observed that for polycrystalline alloys with a high area coverage of preferential grains for microstrain, the mechanical properties (ductility) of magnetostrictive alloys can be significantly improved. Targeted metallurgical processing steps promote abnormal grain growth of {011} grains in galfenol and alfenol thin sheets, which contain two easy axes for magnetic domain alignment during magnetostriction. This can be accomplished by adding particles such as boride species [13] and niobium carbide (NbC) [14] during initial chill casting of the ingot.

For a polycrystalline alloy, an established formula for the magnetostriction, λ, from known directional microstrain measurements is:[15]

λs = 1/5(2λ100+3λ111)

Magnetostrictive alloy deformed to fracture

During subsequent hot rolling and recrystallization steps, particle strengthening occurs in which the particles introduce a “pinning” force at grain boundaries that hinders normal (stochastic) grain growth in an annealing step assisted by a H
2S atmosphere. Thus, single-crystal-like texture (~90% {011} grain coverage) is attainable, reducing the interference with magnetic domain alignment and increasing microstrain attainable for polycrystalline alloys as measured by semiconducting strain gauges.[16] These surface textures can be visualized using electron backscatter diffraction (EBSD) or related diffraction techniques.

Compressive stress to induce domain alignment

For actuator applications, maximum rotation of magnetic moments leads to the highest possible magnetostriction output. This can be achieved by processing techniques such as stress annealing and field annealing. However, mechanical pre-stresses can also be applied to thin sheets to induce alignment perpendicular to actuation as long as the stress is below the buckling limit. For example, it has been demonstrated that applied compressive pre-stress of up to ~50 MPa can result in an increase of magnetostriction by ~90%. This is hypothesized to be due to a "jump" in initial alignment of domains perpendicular to applied stress and improved final alignment parallel to applied stress.[17]

Constitutive behavior of magnetostrictive materials

These materials generally show non-linear behavior with a change in applied magnetic field or stress. For small magnetic fields, linear piezomagnetic constitutive[18] behavior is enough. Non-linear magnetic behavior is captured using a classical macroscopic model such as the Preisach model[19] and Jiles-Atherton model.[20] For capturing magneto-mechanical behavior, Armstrong[21] proposed an "energy average" approach. More recently, Wahi et al.[22] have proposed a computationally efficient constitutive model wherein constitutive behavior is captured using a "locally linearizing" scheme.

Applications

See also

References

  1. ↑ Joule, J.P. (1847). "On the Effects of Magnetism upon the Dimensions of Iron and Steel Bars". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 30, Third Series: 76–87, 225–241. https://books.google.com/books?id=VEgEAAAAYAAJ&q=joule%20annals%20electricity%20219%201842&pg=PA76. Retrieved 2009-07-19.  Joule observed in this paper that he first reported the measurements in a "conversazione" in Manchester, England, in Joule, James (1842). "On a new class of magnetic forces". Annals of Electricity, Magnetism, and Chemistry 8: 219–224. 
  2. ↑ Questions & answers on everyday scientific phenomena. Sctritonscience.com. Retrieved on 2012-08-11.
  3. ↑ James, R. D.; Wuttig, Manfred (12 August 2009). "Magnetostriction of martensite". Philosophical Magazine A 77 (5): 1273–1299. doi:10.1080/01418619808214252. 
  4. ↑ Szewczyk, R. (2006). "Modelling of the magnetic and magnetostrictive properties of high permeability Mn-Zn ferrites". PRAMANA-Journal of Physics 67 (6): 1165–1171. doi:10.1007/s12043-006-0031-z. Bibcode: 2006Prama..67.1165S. 
  5. ↑ "Magnetostriction and Magnetostrictive Materials". UCLA. http://aml.seas.ucla.edu/research/areas/magnetostrictive/mag-composites/Magnetostriction%20and%20Magnetostrictive%20Materials.htm. 
  6. ↑ Park, Jung Jin; Na, Suok-Min; Raghunath, Ganesh; Flatau, Alison B. (March 2016). "Stress-anneal-induced magnetic anisotropy in highly textured Fe-Ga and Fe-Al magnetostrictive strips for bending-mode vibrational energy harvesters". AIP Advances 6 (5): 056221. doi:10.1063/1.4944772. Bibcode: 2016AIPA....6e6221P. 
  7. ↑ Olabi, A.G.; Grunwald, A. (January 2008). "Design and application of magnetostrictive materials". Materials & Design 29 (2): 469–483. doi:10.1016/j.matdes.2006.12.016. http://doras.dcu.ie/15063/1/Olabi-MS-paper-12-09-06.pdf. 
  8. ↑ Turtelli, R Sato; Kriegisch, M; Atif, M; Grössinger, R (17 June 2014). "Co-ferrite – A material with interesting magnetic properties". IOP Conference Series: Materials Science and Engineering 60 (1): 012020. doi:10.1088/1757-899X/60/1/012020. Bibcode: 2014MS&E...60a2020T. 
  9. ↑ Slonczewski, J. C. (15 June 1958). "Origin of Magnetic Anisotropy in Cobalt-Substituted Magnetite". Physical Review 110 (6): 1341–1348. doi:10.1103/PhysRev.110.1341. Bibcode: 1958PhRv..110.1341S. 
  10. ↑ Lo, C.C.H.; Ring, A.P.; Snyder, J.E.; Jiles, D.C. (October 2005). "Improvement of magnetomechanical properties of cobalt ferrite by magnetic annealing". IEEE Transactions on Magnetics 41 (10): 3676–3678. doi:10.1109/TMAG.2005.854790. Bibcode: 2005ITM....41.3676L. 
  11. ↑ Wang, Jiquan; Gao, Xuexu; Yuan, Chao; Li, Jiheng; Bao, Xiaoqian (March 2016). "Magnetostriction properties of oriented polycrystalline CoFe 2 O 4". Journal of Magnetism and Magnetic Materials 401: 662–666. doi:10.1016/j.jmmm.2015.10.073. Bibcode: 2016JMMM..401..662W. 
  12. ↑ Aubert, A.; Loyau, V.; Mazaleyrat, F.; LoBue, M. (August 2017). "Uniaxial anisotropy and enhanced magnetostriction of CoFe 2 O 4 induced by reaction under uniaxial pressure with SPS". Journal of the European Ceramic Society 37 (9): 3101–3105. doi:10.1016/j.jeurceramsoc.2017.03.036. https://hal.archives-ouvertes.fr/hal-01636264. 
  13. ↑ Li, J.H.; Gao, X.X.; Xie, J.X.; Yuan, C.; Zhu, J.; Yu, R.B. (July 2012). "Recrystallization behavior and magnetostriction under pre-compressive stress of Fe–Ga–B sheets". Intermetallics 26: 66–71. doi:10.1016/j.intermet.2012.02.019. 
  14. ↑ Na, S-M.; Flatau, A.B. (May 2014). "Texture evolution and probability distribution of Goss orientation in magnetostrictive Fe–Ga alloy sheets". Journal of Materials Science 49 (22): 7697–7706. doi:10.1007/s10853-014-8478-7. Bibcode: 2014JMatS..49.7697N. 
  15. ↑ Grössinger, R.; Turtelli, R. Sato; Mahmood, N. (2014). "Materials with high magnetostriction". IOP Conference Series: Materials Science and Engineering 60 (1): 012002. doi:10.1088/1757-899X/60/1/012002. Bibcode: 2014MS&E...60a2002G. 
  16. ↑ Na, S-M.; Flatau, A.B. (May 2014). "Texture evolution and probability distribution of Goss orientation in magnetostrictive Fe–Ga alloy sheets". Journal of Materials Science 49 (22): 7697–7706. doi:10.1007/s10853-014-8478-7. Bibcode: 2014JMatS..49.7697N. 
  17. ↑ Downing, J; Na, S-M; Flatau, A (January 2017). "Compressive pre-stress effects on magnetostrictive behaviors of highly textured Galfenol and Alfenol thin sheets". AIP Advances 7 (5): 056420. doi:10.1063/1.4974064. 056420. Bibcode: 2017AIPA....7e6420D. 
  18. ↑ Isaak D, Mayergoyz (1999). Handbook of giant magnetostrictive materials. Elsevier. 
  19. ↑ Preisach, F. (May 1935). "Über die magnetische Nachwirkung" (in de). Zeitschrift für Physik 94 (5–6): 277–302. doi:10.1007/BF01349418. ISSN 1434-6001. Bibcode: 1935ZPhy...94..277P. http://link.springer.com/10.1007/BF01349418. 
  20. ↑ Jiles, D. C.; Atherton, D. L. (1984-03-15). "Theory of ferromagnetic hysteresis (invited)" (in en). Journal of Applied Physics 55 (6): 2115–2120. doi:10.1063/1.333582. ISSN 0021-8979. Bibcode: 1984JAP....55.2115J. http://aip.scitation.org/doi/10.1063/1.333582. 
  21. ↑ Armstrong, William D. (1997-04-15). "Burst magnetostriction in Tb0.3Dy0.7Fe1.9" (in en). Journal of Applied Physics 81 (8): 3548–3554. doi:10.1063/1.364992. ISSN 0021-8979. Bibcode: 1997JAP....81.3548A. http://aip.scitation.org/doi/10.1063/1.364992. 
  22. ↑ Wahi, Sajan K.; Kumar, Manik; Santapuri, Sushma; Dapino, Marcelo J. (2019-06-07). "Computationally efficient locally linearized constitutive model for magnetostrictive materials" (in en). Journal of Applied Physics 125 (21): 215108. doi:10.1063/1.5086953. ISSN 0021-8979. Bibcode: 2019JAP...125u5108W. http://aip.scitation.org/doi/10.1063/1.5086953. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Magnetostriction&oldid=3417304"