Physics:Relative humidity

From HandWiki
Humidity and hygrometry
Cloud forest mount kinabalu.jpg
Specific concepts
General concepts
Measures and Instruments

Relative humidity (RH) is the ratio of the partial pressure of water vapor to the equilibrium vapor pressure of water at a given temperature. Relative humidity depends on temperature and the pressure of the system of interest. The same amount of water vapor results in higher relative humidity in cool air than warm air. A related parameter is the dew point.

Definition

The relative humidity [math]\displaystyle{ (RH }[/math] or [math]\displaystyle{ \phi) }[/math] of an air–water mixture is defined as the ratio of the partial pressure of water vapor [math]\displaystyle{ (p_\mathrm{H_2O}) }[/math] in the mixture to the equilibrium vapor pressure of water [math]\displaystyle{ (p^*_\mathrm{H_2O}) }[/math] over a flat surface of pure water[1] at a given temperature:[2][3]

[math]\displaystyle{ \phi = \frac{p_\mathrm{H_2O}}{p^*_\mathrm{H_2O}}. }[/math]

Relative humidity is normally expressed as a percentage; a higher percentage means that the air–water mixture is more humid. At 100% relative humidity, the air is saturated and is at its dew point.

Significance

Climate control

Climate control refers to the control of temperature and relative humidity in buildings, vehicles and other enclosed spaces for the purpose of providing for human comfort, health and safety, and of meeting environmental requirements of machines, sensitive materials (for example, historic) and technical processes.

Relative humidity and thermal comfort

Along with air temperature, mean radiant temperature, air speed, metabolic rate, and clothing level, relative humidity plays a role in human thermal comfort. According to ASHRAE Standard 55-2017: Thermal Environmental Conditions for Human Occupancy, indoor thermal comfort can be achieved through the PMV method with relative humidities ranging from 0–100%, depending on the levels of the other factors contributing to thermal comfort.[4] However, the recommended range of indoor relative humidity in air conditioned buildings is generally 30–60%.[5][6]

In general, higher temperatures will require lower relative humidities to achieve thermal comfort compared to lower temperatures, with all other factors held constant. For example, with clothing level = 1, metabolic rate = 1.1, and air speed 0.1 m/s, a change in air temperature and mean radiant temperature from 20 °C to 24 °C would lower the maximum acceptable relative humidity from 100% to 65% to maintain thermal comfort conditions. The CBE Thermal Comfort Tool can be used to demonstrate the effect of relative humidity for specific thermal comfort conditions and it can be used to demonstrate compliance with ASHRAE Standard 55-2017.[7]

When using the adaptive model to predict thermal comfort indoors, relative humidity is not taken into account.[4]

Although relative humidity is an important factor for thermal comfort, humans are more sensitive to variations in temperature than they are to changes in relative humidity.[8] Relative humidity has a small effect on thermal comfort outdoors when air temperatures are low, a slightly more pronounced effect at moderate air temperatures, and a much stronger influence at higher air temperatures.[9]

Human discomfort caused by low relative humidity

In cold climates, the outdoor temperature causes lower capacity for water vapor to flow about. Although it may be snowing and the relative humidity outdoors is high, once that air comes into a building and heats up, its new relative humidity is very low (meaning the air is very dry), which can cause discomfort. Dry cracked skin can result from dry air.

Low humidity causes tissue lining nasal passages to dry, crack and become more susceptible to penetration of Rhinovirus cold viruses.[10] Low humidity is a common cause of nosebleeds. The use of a humidifier in homes, especially bedrooms, can help with these symptoms.[11]

Indoor relative humidities should be kept above 30% to reduce the likelihood of the occupant's nasal passages drying out.[12][13]

Humans can be comfortable within a wide range of humidities depending on the temperature—from 30–70%[14]—but ideally between 50 %[15] and 60 %.[16] Very low humidity can create discomfort, respiratory problems, and aggravate allergies in some individuals. In the winter, it is advisable to maintain relative humidity at 30% or above.[17] Extremely low (below 20 %) relative humidities may also cause eye irritation.[12][18]

Buildings

For climate control in buildings using HVAC systems, the key is to maintain the relative humidity at a comfortable range—low enough to be comfortable but high enough to avoid problems associated with very dry air.

When the temperature is high and the relative humidity is low, evaporation of water is rapid; soil dries, wet clothes hung on a line or rack dry quickly, and perspiration readily evaporates from the skin. Wooden furniture can shrink, causing the paint that covers these surfaces to fracture.

When the temperature is low and the relative humidity is high, evaporation of water is slow. When relative humidity approaches 100 %, condensation can occur on surfaces, leading to problems with mold, corrosion, decay, and other moisture-related deterioration. Condensation can pose a safety risk as it can promote the growth of mold and wood rot as well as possibly freezing emergency exits shut.

Certain production and technical processes and treatments in factories, laboratories, hospitals, and other facilities require specific relative humidity levels to be maintained using humidifiers, dehumidifiers and associated control systems.

Vehicles

The basic principles for buildings, above, also apply to vehicles. In addition, there may be safety considerations. For instance, high humidity inside a vehicle can lead to problems of condensation, such as misting of windshields and shorting of electrical components. In vehicles and pressure vessels such as pressurized airliners, submersibles and spacecraft, these considerations may be critical to safety, and complex environmental control systems including equipment to maintain pressure are needed.

Aviation

Airliners operate with low internal relative humidity, often under 20 %[19], especially on long flights. The low humidity is a consequence of drawing in the very cold air with a low absolute humidity, which is found at airliner cruising altitudes. Subsequent warming of this air lowers its relative humidity. This causes discomfort such as sore eyes, dry skin, and drying out of mucosa, but humidifiers are not employed to raise it to comfortable mid-range levels because the volume of water required to be carried on board can be a significant weight penalty. As airliners descend from colder altitudes into warmer air (perhaps even flying through clouds a few thousand feet above the ground), the ambient relative humidity can increase dramatically. Some of this moist air is usually drawn into the pressurized aircraft cabin and into other non-pressurized areas of the aircraft and condenses on the cold aircraft skin. Liquid water can usually be seen running along the aircraft skin, both on the inside and outside of the cabin. Because of the drastic changes in relative humidity inside the vehicle, components must be qualified to operate in those environments. The recommended environmental qualifications for most commercial aircraft components is listed in RTCA DO-160.

Cold, humid air can promote the formation of ice, which is a danger to aircraft as it affects the wing profile and increases weight. Carburetor engines have a further danger of ice forming inside the carburetor. Aviation weather reports (METARs) therefore include an indication of relative humidity, usually in the form of the dew point.

Pilots must take humidity into account when calculating takeoff distances, because high humidity requires longer runways and will decrease climb performance.

Density altitude is the altitude relative to the standard atmosphere conditions (International Standard Atmosphere) at which the air density would be equal to the indicated air density at the place of observation, or, in other words, the height when measured in terms of the density of the air rather than the distance from the ground. "Density Altitude" is the pressure altitude adjusted for non-standard temperature.

An increase in temperature, and, to a much lesser degree, humidity, will cause an increase in density altitude. Thus, in hot and humid conditions, the density altitude at a particular location may be significantly higher than the true altitude.

Measurement

A hygrometer is a device used for measuring the humidity of air.

The humidity of an air and water vapor mixture is determined through the use of psychrometric charts if both the dry bulb temperature (T) and the wet bulb temperature (Tw) of the mixture are known. These quantities are readily estimated by using a sling psychrometer.

There are several empirical formulas that can be used to estimate the equilibrium vapor pressure of water vapor as a function of temperature. The Antoine equation is among the least complex of these, having only three parameters (A, B, and C). Other formulas, such as the Goff–Gratch equation and the Magnus–Tetens approximation, are more complicated but yield better accuracy.[citation needed]

The Arden Buck equation[20] is commonly encountered in the literature regarding this topic:

[math]\displaystyle{ e^*_w = (1.0007 + 3.46 \times 10^{-6} P) \times 6.1121\, e^{17.502 T/(240.97 + T)}, }[/math]

where [math]\displaystyle{ T }[/math] is the dry-bulb temperature expressed in degrees Celsius (°C), [math]\displaystyle{ P }[/math] is the absolute pressure expressed in millibars, and [math]\displaystyle{ e^*_w }[/math] is the equilibrium vapor pressure expressed in millibars. Buck has reported that the maximal relative error is less than 0.20% between −20 °C and +50 °C when this particular form of the generalized formula is used to estimate the equilibrium vapor pressure of water.

Water vapor is independent of air

The notion of air "holding" water vapor or being "saturated" by it is often mentioned in connection with the concept of relative humidity. This, however, is misleading—the amount of water vapor that enters (or can enter) a given space at a given temperature is almost independent of the amount of air (nitrogen, oxygen, etc.) that is present. Indeed, a vacuum has approximately the same equilibrium capacity to hold water vapor as the same volume filled with air; both are given by the equilibrium vapor pressure of water at the given temperature.[1][21] There is a very small difference described under "Enhancement factor" below, which can be neglected in many calculations unless high accuracy is required.

Pressure dependence

The relative humidity of an air–water system is dependent not only on the temperature but also on the absolute pressure of the system of interest. This dependence is demonstrated by considering the air–water system shown below. The system is closed (i.e., no matter enters or leaves the system).

Changes in Relative Humidity.png

If the system at State A is isobarically heated (heating with no change in system pressure), then the relative humidity of the system decreases because the equilibrium vapor pressure of water increases with increasing temperature. This is shown in State B.

If the system at State A is isothermally compressed (compressed with no change in system temperature), then the relative humidity of the system increases because the partial pressure of water in the system increases with the volume reduction. This is shown in State C. Above 202.64 kPa, the RH would exceed 100% and water may begin to condense.

If the pressure of State A was changed by simply adding more dry air, without changing the volume, the relative humidity would not change.

Therefore, a change in relative humidity can be explained by a change in system temperature, a change in the volume of the system, or change in both of these system properties.

Enhancement factor

The enhancement factor [math]\displaystyle{ (f_w) }[/math] is defined as the ratio of the saturated vapor pressure of water in moist air [math]\displaystyle{ (e'_w) }[/math] to the saturated vapor pressure of pure water:

[math]\displaystyle{ f_W = \frac{e'_w}{e^*_w}. }[/math]

The enhancement factor is equal to unity for ideal gas systems. However, in real systems the interaction effects between gas molecules result in a small increase of the equilibrium vapor pressure of water in air relative to equilibrium vapor pressure of pure water vapor. Therefore, the enhancement factor is normally slightly greater than unity for real systems.

The enhancement factor is commonly used to correct the equilibrium vapor pressure of water vapor when empirical relationships, such as those developed by Wexler, Goff, and Gratch, are used to estimate the properties of psychrometric systems.

Buck has reported that, at sea level, the vapor pressure of water in saturated moist air amounts to an increase of approximately 0.5% over the equilibrium vapor pressure of pure water.[22]

Related concepts

The term relative humidity is reserved for systems of water vapor in air. The term relative saturation is used to describe the analogous property for systems consisting of a condensable phase other than water in a non-condensable phase other than air.[23]

Other important facts

Relative Humidity.png

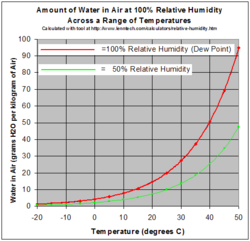
A gas in this context is referred to as saturated when the vapor pressure of water in the air is at the equilibrium vapor pressure for water vapor at the temperature of the gas and water vapor mixture; liquid water (and ice, at the appropriate temperature) will fail to lose mass through evaporation when exposed to saturated air. It may also correspond to the possibility of dew or fog forming, within a space that lacks temperature differences among its portions, for instance in response to decreasing temperature. Fog consists of very minute droplets of liquid, primarily held aloft by isostatic motion (in other words, the droplets fall through the air at terminal velocity, but as they are very small, this terminal velocity is very small too, so it doesn't look to us like they are falling, and they seem to be held aloft).

The statement that relative humidity (RH %) can never be above 100 %, while a fairly good guide, is not absolutely accurate, without a more sophisticated definition of humidity than the one given here. Cloud formation, in which aerosol particles are activated to form cloud condensation nuclei, requires the supersaturation of an air parcel to a relative humidity of slightly above 100 %. One smaller-scale example is found in the Wilson cloud chamber in nuclear physics experiments, in which a state of supersaturation is induced to accomplish its function.

For a given dew point and its corresponding absolute humidity, the relative humidity will change inversely, albeit nonlinearly, with the temperature. This is because the partial pressure of water increases with temperature—the operative principle behind everything from hair dryers to dehumidifiers.

Due to the increasing potential for a higher water vapor partial pressure at higher air temperatures, the water content of air at sea level can get as high as 3% by mass at 30 °C (86 °F) compared to no more than about 0.5% by mass at 0 °C (32 °F). This explains the low levels (in the absence of measures to add moisture) of humidity in heated structures during winter, resulting in dry skin, itchy eyes, and persistence of static electric charges. Even with saturation (100% relative humidity) outdoors, heating of infiltrated outside air that comes indoors raises its moisture capacity, which lowers relative humidity and increases evaporation rates from moist surfaces indoors (including human bodies and household plants.)

Similarly, during summer in humid climates a great deal of liquid water condenses from air cooled in air conditioners. Warmer air is cooled below its dew point, and the excess water vapor condenses. This phenomenon is the same as that which causes water droplets to form on the outside of a cup containing an ice-cold drink.

A useful rule of thumb is that the maximum absolute humidity doubles for every 20 °F or 10 °C increase in temperature. Thus, the relative humidity will drop by a factor of 2 for each 20 °F or 10 °C increase in temperature, assuming conservation of absolute moisture. For example, in the range of normal temperatures, air at 68 °F or 20 °C and 50% relative humidity will become saturated if cooled to 50 °F or 10 °C, its dew point, and 41 °F or 5 °C air at 80% relative humidity warmed to 68 °F or 20 °C will have a relative humidity of only 29% and feel dry. By comparison, thermal comfort standard ASHRAE 55 requires systems designed to control humidity to maintain a dew point of 16.8 °C (62.2 °F) though no lower humidity limit is established.[24]

Water vapor is a lighter gas than other gaseous components of air at the same temperature, so humid air will tend to rise by natural convection. This is a mechanism behind thunderstorms and other weather phenomena. Relative humidity is often mentioned in weather forecasts and reports, as it is an indicator of the likelihood of precipitation, dew, or fog. In hot summer weather, it also increases the apparent temperature to humans (and other animals) by hindering the evaporation of perspiration from the skin as the relative humidity rises. This effect is calculated as the heat index or humidex.

A device used to measure humidity is called a hygrometer; one used to regulate it is called a humidistat, or sometimes hygrostat. (These are analogous to a thermometer and thermostat for temperature, respectively.)

See also

References

  1. ↑ 1.0 1.1 "Water Vapor Myths: A Brief Tutorial". Archived from the original on 2016-01-25. https://web.archive.org/web/20160125031338/http://www.atmos.umd.edu/~stevenb/vapor/. 
  2. ↑ Perry, R. H. and Green, D. W, Perry's Chemical Engineers' Handbook (7th Edition), McGraw-Hill, ISBN:0-07-049841-5 , Eqn 12-7
  3. ↑ Lide, David (2005). CRC Handbook of Chemistry and Physics (85 ed.). CRC Press. pp. 15–25. ISBN 0-8493-0485-7. https://archive.org/details/crchandbookofche81lide/page/15. 
  4. ↑ 4.0 4.1 ASHRAE Standard 55 (2017). "Thermal Environmental Conditions for Human Occupancy".
  5. ↑ Wolkoff, Peder; Kjaergaard, Søren K. (August 2007). "The dichotomy of relative humidity on indoor air quality". Environment International 33 (6): 850–857. doi:10.1016/j.envint.2007.04.004. ISSN 0160-4120. PMID 17499853. 
  6. ↑ ASHRAE Standard 160 (2016). "Criteria for Moisture-Control Design Analysis in Buildings"
  7. ↑ Schiavon, Stefano; Hoyt, Tyler; Piccioli, Alberto (2013-12-27). "Web application for thermal comfort visualization and calculation according to ASHRAE Standard 55" (in en). Building Simulation 7 (4): 321–334. doi:10.1007/s12273-013-0162-3. ISSN 1996-3599. http://www.escholarship.org/uc/item/4db4q37h. 
  8. ↑ Fanger, P. O. (1970). Thermal comfort: analysis and applications in environmental engineering. Danish Technical Press. 
  9. ↑ Bröde, Peter; Fiala, Dusan; Błażejczyk, Krzysztof; Holmér, Ingvar; Jendritzky, Gerd; Kampmann, Bernhard; Tinz, Birger; Havenith, George (2011-05-31). "Deriving the operational procedure for the Universal Thermal Climate Index (UTCI)" (in en). International Journal of Biometeorology 56 (3): 481–494. doi:10.1007/s00484-011-0454-1. ISSN 0020-7128. PMID 21626294. http://rcin.org.pl/Content/29015. 
  10. ↑ "Archived copy". Archived from the original on 2016-02-04. https://web.archive.org/web/20160204170937/https://www.urmc.rochester.edu/Encyclopedia/Content.aspx?ContentTypeID=85&ContentID=P00620. Retrieved 2016-01-24.  University of Rochester Medical Center | What causes the common cold? | Health Encyclopedia
  11. ↑ "Archived copy". Archived from the original on 2015-11-10. https://web.archive.org/web/20151110084258/http://www.webmd.com/first-aid/tc/nosebleeds-prevention. Retrieved 2015-11-01.  Nosebleeds - Prevention | WebMD Medical Reference
  12. ↑ 12.0 12.1 Arundel, A. V.; Sterling, E. M.; Biggin, J. H.; Sterling, T. D. (1986). "Indirect health effects of relative humidity in indoor environments". Environ. Health Perspect. 65: 351–61. doi:10.1289/ehp.8665351. PMID 3709462. 
  13. ↑ "Indoor Air Quality". NH DHHS, Division of Public Health Services. Archived from the original on 2015-09-22. https://web.archive.org/web/20150922045933/http://www.dhhs.nh.gov/dphs/holu/documents/hom-airindoor.pdf. Retrieved 2016-01-24. 
  14. ↑ Gilmore, C. P. (September 1972). "More Comfort for Your Heating Dollar". Popular Science: 99. 
  15. ↑ "Winter Indoor Comfort and Relative Humidity", Information please, Pearson, 2007, archived from the original on 2013-04-27, https://web.archive.org/web/20130427093228/http://www.infoplease.com/ipa/A0001412.html, retrieved 2013-05-01, "…by increasing the relative humidity to above 50% within the above temperature range, 80% or more of all average dressed persons would feel comfortable." 
  16. ↑ "Recommended relative humidity level", The engineering toolbox, archived from the original on 2013-05-11, https://web.archive.org/web/20130511044413/http://www.engineeringtoolbox.com/relative-humidity-d_895.html, retrieved 2013-05-01, "Relative humidity above 60% feels uncomfortable wet. Human comfort requires the relative humidity to be in the range 25–60% RH." 
  17. ↑ "Archived copy". Archived from the original on 2015-01-20. https://web.archive.org/web/20150120050352/http://www.doh.wa.gov/Portals/1/Documents/Pubs/333-044.pdf. Retrieved 2015-11-01.  School Indoor Air Quality | Best Management Practices Manual | November 2003 | Office | Office of Environmental Health and Safety | Indoor Air Quality Program DOH 333-044 November 2003 | Washington State Department of Health
  18. ↑ "Indoor air quality testing". Archived from the original on 2017-09-21. https://web.archive.org/web/20170921045630/https://watertreatmentservices.co.uk/air/indoor-air-quality-assessment/. 
  19. ↑ https://www.aviatoratlas.com/posts/airplane-humidity
  20. ↑ Buck, Arden (December 1981). "New Equations for Computing Vapor Pressure and Enhancement Factor". National Center for Atmospheric Research. Archived from the original on March 4, 2016. https://web.archive.org/web/20160304093405/http://www.public.iastate.edu/~bkh/teaching/505/arden_buck_sat.pdf. Retrieved July 21, 2017. 
  21. ↑ Fraser, Alistair B.. "Bad Clouds FAQ". Archived from the original on 2006-06-17. https://web.archive.org/web/20060617034620/http://www.ems.psu.edu/~fraser/Bad/BadFAQ/BadCloudsFAQ.html. 
  22. ↑ Buck, A. L. (1981). "New Equations for Computing Vapor Pressure and Enhancement Factor". Journal of Applied Meteorology 20 (12): 1527–1532. doi:10.1175/1520-0450(1981)020<1527:NEFCVP>2.0.CO;2. Bibcode: 1981JApMe..20.1527B. 
  23. ↑ "Vapor-Liquid/Solid System, 201 Class Page". University of Arizona. http://blowers.chee.arizona.edu/201project/GLsys.interrelatn.pg1.HTML. 
  24. ↑ "Thermal Environmental Conditions for Human Occupancy". ASHRAE Standard 55. 2013. 
General
  • Himmelblau, David M. (1989). Basic Principles And Calculations In Chemical Engineering. Prentice Hall. ISBN 0-13-066572-X. 
  • Perry, R.H. & Green, D.W (1997). Perry's Chemical Engineers' Handbook (7th Edition). McGraw-Hill. ISBN 0-07-049841-5. 

External links




Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Relative_humidity&oldid=300790"