Physics:Resistive pulse sensing

Resistive pulse sensing (RPS) is the generic, non-commercial term given for the well-developed technology used to detect, and measure the size of, individual particles in fluid. First invented by Wallace H. Coulter in 1953, the RPS technique is the basic principle behind the Coulter Principle, which is a trademark term. Resistive pulse sensing is also known as the electrical zone sensing technique, reflecting its fundamentally electrical nature, which distinguishes it from other particle sizing technologies such as the optically-based dynamic light scattering (DLS) and nanoparticle tracking analysis (NTA). An international standard has been developed for the use of the resistive pulse sensing technique by the International Organization for Standardization.

Construction and operation

Fig. 1. Schematic diagram for resistive pulse sensing, in which particles, suspended in a weakly conducting fluid, flow through a nanoconstriction, and are sensed electrically by electrodes placed on either side of the nanoconstriction.

Fig. 2. Line drawing of resistive pulse sensing time-based schematic data. A single particle passing through a constriction causes a momentary change in the electrical resistance, proportional to the particle volume.

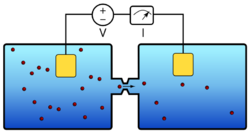
The basic design principle underlying resistive pulse sensing is shown in Fig. 1. Individual particles, suspended in a conductive fluid, flow one-at-a-time through a constriction. The fluids most commonly used are water containing some amount of dissolved salts, sufficient to carry an electrical current. The salinity levels of seawater or of a wide range of concentrations of phosphate-buffered saline are easily sufficient for this purpose, with electrical conductivity in the mS-S range and salt concentrations of order 1 percent. Typical tap water often contains sufficient dissolved minerals to conduct sufficiently for this application as well.

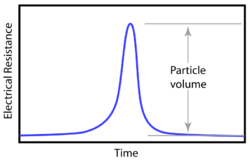
Electrical contact is made with the fluid using metal electrodes, in the best case using platinum or other low electrode potential metals, as are found in electrochemical cell constructions. Biasing the electrodes with an electrical potential of order 1 volt will cause an electrical current to flow through the fluid. If properly designed, the electrical resistance of the constriction will dominate in the total electrical resistance of the circuit. Particles that flow through the constriction while the electrical current is being monitored will cause an obscuration of that current, resulting in an increase in the voltage drop between the two electrodes. In other words, the particle causes a change in the electrical resistance of the constriction. The change in the electrical resistance as a particle passes through a constriction is shown schematically in Fig. 2.

Theory of operation

The quantitative relationship between the measured change in electrical resistance and the size of the particle that caused that change was worked out by De Blois and Bean in 1970. De Blois and Bean found the very simple result that the resistance change [math]\displaystyle{ \Delta R }[/math] is proportional to the ratio of particle volume [math]\displaystyle{ V_p }[/math] to the effective volume [math]\displaystyle{ V_c }[/math] of the constriction: [math]\displaystyle{ \Delta R = A \frac{V_p}{V_c} }[/math], where [math]\displaystyle{ A }[/math] is a factor that depends on the detailed geometry of the constriction and the electrical conductivity of the working fluid.

Hence, by monitoring the electrical resistance as indicated by changes in the voltage drop across the constriction, one can count particles, as each increase in resistance indicates passage of a particle through the constriction, and one can measure the size of that particle, as the magnitude of the resistance change during the particle passage is proportional to that particle's volume. As one can usually calculate the volumetric flow rate of fluid through the constriction, controlled externally by setting the pressure difference across the constriction, one can then calculate the concentration of particles. With a large enough number of particle transients to provide adequate statistical significance, the concentration as a function of particle size, also known as the concentration spectral density, with units of per volume fluid per volume particle, can be calculated.

Minimum detectable size and dynamic range

Two important considerations when evaluating a resistive pulse sensing (RPS) instrument are the minimum detectable particle size and the dynamic range of the instrument. The minimum detectable size is determined by the volume [math]\displaystyle{ V_c }[/math] of the constriction, the voltage difference applied across that constriction, and the noise of the first-stage amplifier used to detect the particle signal. In other words, one must evaluate the minimum signal-to-noise ratio of the system. The minimum particle size can be defined as the size of the particle that generates a signal whose magnitude is equal to the noise, integrated over the same frequency bandwidth as generated by the signal. The dynamic range of an RPS instrument is set at its upper end by the diameter of the constriction, as that is the maximum size particle that can pass through the constriction. One can also instead choose a somewhat smaller maximum, perhaps setting it to 70 percent of this maximum volume. The dynamic range is then equal to the ratio of the maximum particle size to the minimum detectable size. This ratio can be quoted either as the ratio of the maximum to minimum particle volume, or as the ratio of the maximum to minimum particle diameter (the cube of the first method).

Microfluidic resistive pulse sensing (MRPS)

The original Coulter counter was originally designed using a special technology to fabricate small pores in glass volumes, but the expense and complexity of fabricating these elements means they become a semi-permanent part of the analytic RPS instrument. This also limited the minimum diameter constrictions that could be reliably fabricated, making the RPS technique challenging to use for particles below roughly 1 micron in diameter.

There was therefore significant interest in applying the fabrication techniques developed for microfluidic circuits to RPS sensing. This translation of RPS technology to the microfluidic domain enables very small constrictions, well below effective diameters of 1 micron; this therefore extends the minimum detectable particle size to the deep sub-micron range. Using microfluidics technology also allows the use of inexpensive cast plastic or elastomer parts for defining the critical constriction component, which also become disposable. The use of a disposable element eliminates concerns about sample cross-contamination as well as obviating the need for time-consuming cleaning of the RPS instrument. Scientific advances demonstrating these capabilities have been published in the scientific literature, such as by Kasianowicz et al., Saleh and Sohn, and Fraikin et al. These together illustrate a variety of methods to fabricate microfluidic or lab-on-a-chip versions of the Coulter counter technology.