Physics:Self-buckling

From HandWiki
Short description: Concept in mechanical engineering

A column can buckle due to its own weight with no other direct forces acting on it, in a failure mode called self-buckling. In conventional column buckling problems, the self-weight is often neglected since it is assumed to be small when compared to the applied axial loads. However, when this assumption is not valid, it is important to take the self-buckling into account.

Elastic buckling of a "heavy" column i.e., column buckling under its own weight, was first investigated by Greenhill in 1881.[1] He found that a free-standing, vertical column, with density [math]\displaystyle{ \rho }[/math], Young's modulus [math]\displaystyle{ E }[/math], and cross-sectional area [math]\displaystyle{ A }[/math], will buckle under its own weight if its height exceeds a certain critical value:

[math]\displaystyle{ l_\text{max} \approx \left(7.8373\,\frac{EI}{\rho gA}\right)^\frac{1}{3} }[/math]

where [math]\displaystyle{ g }[/math] is the acceleration due to gravity, [math]\displaystyle{ I }[/math] is the second moment of area of the beam cross section.

One interesting example for the use of the equation was suggested by Greenhill in his paper. He estimated the maximal height of a pine tree, and found it cannot grow over 300-ft tall. This length sets the maximum height for trees on earth if we assume the trees to be prismatic and the branches are neglected.

Mathematical derivation

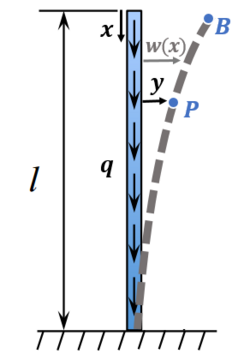
A column exhibiting a compressive buckling load due to its own weight.

Suppose a uniform column fixed in a vertical direction at its lowest point, and carried to a height [math]\displaystyle{ l }[/math], in which the vertical position becomes unstable and flexure begins. There is a body force [math]\displaystyle{ q }[/math] per unit length [math]\displaystyle{ q = \rho g A }[/math], where [math]\displaystyle{ A }[/math] is the cross-sectional area of the column, [math]\displaystyle{ g }[/math] is the acceleration due to gravity and [math]\displaystyle{ \rho }[/math] is its mass density.

The column is slightly curved under its own weight, so the curve [math]\displaystyle{ w(x) }[/math] describes the deflection of the beam in the [math]\displaystyle{ y }[/math] direction at some position [math]\displaystyle{ x }[/math]. Looking at any point on the column, we can write the moment equilibrium:

[math]\displaystyle{ M = -\int_0^x q(y - w)\mathrm{d}x }[/math]

where the right-hand side of the equation is the moment of the weight of BP about P.

According to Euler–Bernoulli beam theory:

[math]\displaystyle{ M = -EI{\mathrm{d}^2w \over \mathrm{d}x^2} }[/math]

Where [math]\displaystyle{ E }[/math] is the Young's modulus of elasticity of the substance, [math]\displaystyle{ I }[/math] is the second moment of area.

Therefore, the differential equation of the central line of BP is:[math]\displaystyle{ }[/math][math]\displaystyle{ }[/math]

[math]\displaystyle{ EI{\mathrm{d}^2w \over \mathrm{d}x^2} = q\int_0^x (y - w)\mathrm{d}x }[/math]

Differentiating with respect to x, we get

[math]\displaystyle{ \begin{align} EI{\mathrm{d}^3w \over \mathrm{d}x^3} &= q\int_0^x \left(-{\mathrm{d}w \over \mathrm{d}x}\right)\mathrm{d}x \\ &= -qx {\mathrm{d}w \over \mathrm{d}x} \end{align} }[/math]

We get that the governing equation is the third order linear differential equation with a variable coefficient. The way to solve the problem is to use new variables [math]\displaystyle{ n, z, k }[/math] and [math]\displaystyle{ r }[/math]:

[math]\displaystyle{ k^2 = {4 \over 9}{q \over EI},\quad r^2 = x^3,\quad \sqrt{x} z = {\mathrm{d}w \over \mathrm{d}x},\quad n^2 = {1 \over 3^2} }[/math]

Then, the equation transforms to the Bessel equation

[math]\displaystyle{ r^2 {\mathrm{d}^2z \over \mathrm{d}r^2} + r{\mathrm{d}z \over \mathrm{d}r} + \left(k^2 r^2 - n^2\right)z = 0 }[/math]

The solution of the transformed equation is [math]\displaystyle{ z = AJ_\frac{1}{3}(kr) + BJ_{-\frac{1}{3}}(kr) }[/math]

Where [math]\displaystyle{ J_n }[/math] is the Bessel function of the first kind. Then, the solution of the original equation is:

[math]\displaystyle{ {\mathrm{d}w \over \mathrm{d}x} = \sqrt{x}\left(AJ_\frac{1}{3} \left(kx^{\frac{3}{2}}\right) + BJ_{-\frac{1}{3},1} \left(kx^{\frac{3}{2}}\right)\right) }[/math]

Now, we will use the boundary conditions:

  • No moment at [math]\displaystyle{ x = 0 \rightarrow {\mathrm{d}^2 w \over \mathrm{d}x^2}(x = 0) = 0 \rightarrow A = 0 }[/math]
  • Fixed at [math]\displaystyle{ x = l \rightarrow w(l) = 0 \rightarrow J_{-\frac{1}{3}} \left(kl^{\frac{3}{2}}\right) = 0 }[/math]

From the second B.C., we get that the critical length in which a vertical column will buckle under its own weight is:

[math]\displaystyle{ l_\text{max} = \left(\frac{j_{\frac{1}{3},1}}{k}\right)^\frac{2}{3} = \left(\frac{9 {j_{\frac{1}{3},1}}^2}{4} \frac{EI}{q}\right)^\frac{1}{3} }[/math]

Using [math]\displaystyle{ j_{\frac{1}{3},1} \approx 1.86635 }[/math] , the first zero of the Bessel function of the first kind of order [math]\displaystyle{ -\frac{1}{3} }[/math], [math]\displaystyle{ l_\text{max} }[/math] can be approximated to:

[math]\displaystyle{ l_\text{max} \approx \left(7.8373\,\frac{EI}{\rho gA}\right)^\frac{1}{3} }[/math]

Euler's mistake

The column under its own weight was considered by Euler in three famous papers (1778a, 1778b, 1778c).[2][3][4] In his first paper, Euler (1778a) concluded that the column simply supported under its own weight would never lose its stability. In his second paper on this topic Euler (1778b) described his previous result as paradoxical and suspicious (see Panovko and Gubanova (1965); Nicolai, (1955);[5] Todhunter and Pierson (1866)[6] on this topic). In the next, third in series, paper, Euler (1778c) found that he had made a conceptual mistake and the “infinite buckling load” conclusion was proved to be wrong. Unfortunately, however, he made a numerical mistake and instead of the first eigenvalue, he calculated a second one. Correct solutions were derived by Dinnik (1912),[7] 132 years later, as well as Willers (1941),[8] Engelhardt (1954)[9] and Frich-Fay (1966).[10] Numerical solution with arbitrary accuracy was given by Eisenberger (1991).[11]

222 years later, after Euler's mistake in 1778, in the year 2000, Elishakoff [12][13] revisited this famous problem and derived closed-form solutions for the first time, for self-buckling problems, by resorting to semi-inverse method. Numerous other problems are treated in his monograph.[14]

See also

External links

References

  1. ↑ "Greenhill, A. G. (1881). "Determination of the greatest height consistent with stability that a vertical pole or mast can be made, and the greatest height to which a tree of given proportions can grow." Proc. Cambridge Philos. Soc., 4, 65–73.". https://martingillie.files.wordpress.com/2013/11/longest-column.pdf. 
  2. ↑ Euler, L. (1778a) Determinatio onerum, quae columnae gestare valent, Acta Academiae Scientiarum Petropolitanae, Vol. 1, 121-145 (in Latin).
  3. ↑ Euler, L. (1778b) Examen insignis puradoxi in theoria columnarum occurentis, Acta Academiae Scientiarum Petropolitanae, Vol. 1, 146-162 (in Latin).
  4. ↑ Euler, L. (1778c) De Altitudine columnarum sub proprio pondere corruentium, Acta Academiae Scientiarum Petropolitanae, Vol. 1, 163-193 (in Latin).
  5. ↑ Nicolai, E.V., Works in Mechanics, pp.436-454, Gostekhizdat, Moscow, 1955 (in Russian).
  6. ↑ Todhunter, I. and Pearson K., History of the Theory of Elasticity, Vol. 1, pp. 39-50. Cambridge University Press, 1886.
  7. ↑ Dinnik, A.N., Buckling under Own Weight, Proceedings of Don Polytechnical Institute 1 (Part 2), p. 19, 1912 (in Russian).
  8. ↑ Willers, F.A., Das Knicken schwerer Gestänge, ZAMM‐Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 21(1),(1941) 43–51 (in German).
  9. ↑ Engelhardt, H., Die einheitliche Behandlung der Stabknickung mit Beruecksichtung des Stabeigengewichte in den Eulerfaellen 1 bis 4 als Eigenwertproblem, Der Stahlbau, Vol. 23 (4),80–84, 1954 (in German).
  10. ↑ Frich-Fay, R., On the Stability of a Strut under Uniformly Distributed Axial Forces, Int. J. Solids Struct., Vol. 2, 361–369, 1966.
  11. ↑ Eisenberger, M., Buckling Loads for Variable Cross-Section Member with Variable Axial Forces, Int. J. Solids Struct., Vol. 27, 135–143, 1991.
  12. ↑ Elishakoff, I., A Closed Form-Solution for Generalized Euler Problem, Proc. Royal Soc. London, Vol. 456, 2409–2417, 2000.
  13. ↑ Elishakoff, I., Euler's Problem Revisited: 222 Years Later, Meccanica, Vol. 36, 265-272, 2001.
  14. ↑ Elishakoff, I., Eigenvalues of Inhomogeneous Structures: Unusual Closed-Form Solutions of Semi-Inverse Problems, CRC Press, Boca Raton, 2005, XIV + pp. 729; ISBN:0-8493-2892-6.



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Self-buckling&oldid=3417091"