Physics:Sitnikov problem
The Sitnikov problem is a restricted version of the three-body problem named after Russian mathematician Kirill Alexandrovitch Sitnikov that attempts to describe the movement of three celestial bodies due to their mutual gravitational attraction. A special case of the Sitnikov problem was first discovered by the American scientist William Duncan MacMillan in 1911, but the problem as it currently stands wasn't discovered until 1961 by Sitnikov.
Definition
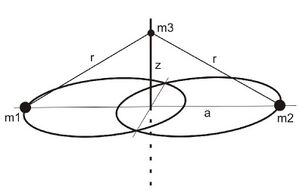
The system consists of two primary bodies with the same mass [math]\displaystyle{ \left(m_1 = m_2 = \tfrac{m}{2}\right) }[/math], which move in circular or elliptical Kepler orbits around their center of mass. The third body, which is substantially smaller than the primary bodies and whose mass can be set to zero [math]\displaystyle{ (m_3 = 0) }[/math], moves under the influence of the primary bodies in a plane that is perpendicular to the orbital plane of the primary bodies (see Figure 1). The origin of the system is at the focus of the primary bodies. A combined mass of the primary bodies [math]\displaystyle{ m = 1 }[/math], an orbital period of the bodies [math]\displaystyle{ 2\pi }[/math], and a radius of the orbit of the bodies [math]\displaystyle{ a = 1 }[/math] are used for this system. In addition, the gravitational constant is 1. In such a system that the third body only moves in one dimension – it moves only along the z-axis.
Equation of motion
In order to derive the equation of motion in the case of circular orbits for the primary bodies, use that the total energy [math]\displaystyle{ \,E }[/math] is:
- [math]\displaystyle{ E=\frac{1}{2}\left(\frac{dz}{dt}\right)^2 - \frac{1}{r} }[/math]
After differentiating with respect to time, the equation becomes:
- [math]\displaystyle{ \frac{d^2z}{dt^2}=-\frac{z}{r^3} }[/math]
This, according to Figure 1, is also true:
- [math]\displaystyle{ r^2 = a^2 + z^2 = 1 + z^2 }[/math]
Thus, the equation of motion is as follows:
- [math]\displaystyle{ \frac{d^2z}{dt^2} = -\frac{z}{\left(\sqrt{1+z^2}\right)^3} }[/math]
which describes an integrable system since it has one degree of freedom.
If on the other hand the primary bodies move in elliptical orbits then the equations of motion are
- [math]\displaystyle{ \frac{d^2z}{dt^2} = -\frac{z}{\left(\sqrt{ \rho(t)^2+z^2}\right)^3} }[/math]
where [math]\displaystyle{ \rho(t) = \rho(t+2 \pi) }[/math] is the distance of either primary from their common center of mass. Now the system has one-and-a-half degrees of freedom and is known to be chaotic.
Significance
Although it is nearly impossible in the real world to find or arrange three celestial bodies exactly as in the Sitnikov problem, the problem is still widely and intensively studied for decades: although it is a simple case of the more general three-body problem, all the characteristics of a chaotic system can nevertheless be found within the problem, making the Sitnikov problem ideal for general studies on effects in chaotic dynamical systems.
See also
Literature
- K. A. Sitnikov: The existence of oscillatory motions in the three-body problems. In: Doklady Akademii Nauk SSSR, 133/1960, pp. 303–306, ISSN 0002-3264 (English Translation in Soviet Physics. Doklady., 5/1960, S. 647–650)
- K. Wodnar: The original Sitnikov article – new insights. In: Celestial Mechanics and Dynamical Astronomy, 56/1993, pp. 99–101, ISSN 0923-2958, pdf
- D. Hevia, F. Rañada: Chaos in the three-body problem: the Sitnikov case. In: European Journal of Physics, 17/1996, pp. 295–302, ISSN 0143-0807, pdf
- Rudolf Dvorak, Florian Freistetter, J. Kurths, Chaos and Stability in Planetary Systems., Springer, 2005, ISBN:3540282084
- J. Moser: "Stable and Random Motion", Princeton Univ. Press, 1973, ISBN:978-0691089102
References
External links
 |