Physics:Three-body problem

From HandWiki
Short description: Physics problem related to laws of motion and gravity
Approximate trajectories of three identical bodies located at the vertices of a scalene triangle and having zero initial velocities. The center of mass, in accordance with the law of conservation of momentum, remains in place.

In physics and classical mechanics, the three-body problem is the problem of taking the initial positions and velocities (or momenta) of three point masses and solving for their subsequent motion according to Newton's laws of motion and Newton's law of universal gravitation.[1] The three-body problem is a special case of the n-body problem. Unlike two-body problems, no general closed-form solution exists,[1] as the resulting dynamical system is chaotic for most initial conditions, and numerical methods are generally required.

Historically, the first specific three-body problem to receive extended study was the one involving the Moon, Earth, and the Sun.[2] In an extended modern sense, a three-body problem is any problem in classical mechanics or quantum mechanics that models the motion of three particles.

Mathematical description

The mathematical statement of the three-body problem can be given in terms of the Newtonian equations of motion for vector positions [math]\displaystyle{ \mathbf{r_i} = (x_i, y_i, z_i) }[/math] of three gravitationally interacting bodies with masses [math]\displaystyle{ m_i }[/math]:

[math]\displaystyle{ \begin{align} \ddot\mathbf{r}_{\mathbf{1}} &= -G m_2 \frac{\mathbf{r_1} - \mathbf{r_2}}{|\mathbf{r_1} - \mathbf{r_2}|^3} - G m_3 \frac{\mathbf{r_1} - \mathbf{r_3}}{|\mathbf{r_1} - \mathbf{r_3}|^3}, \\ \ddot\mathbf{r}_{\mathbf{2}} &= -G m_3 \frac{\mathbf{r_2} - \mathbf{r_3}}{|\mathbf{r_2} - \mathbf{r_3}|^3} - G m_1 \frac{\mathbf{r_2} - \mathbf{r_1}}{|\mathbf{r_2} - \mathbf{r_1}|^3}, \\ \ddot\mathbf{r}_{\mathbf{3}} &= -G m_1 \frac{\mathbf{r_3} - \mathbf{r_1}}{|\mathbf{r_3} - \mathbf{r_1}|^3} - G m_2 \frac{\mathbf{r_3} - \mathbf{r_2}}{|\mathbf{r_3} - \mathbf{r_2}|^3}. \end{align} }[/math]

where [math]\displaystyle{ G }[/math] is the gravitational constant.[3][4] This is a set of nine second-order differential equations. The problem can also be stated equivalently in the Hamiltonian formalism, in which case it is described by a set of 18 first-order differential equations, one for each component of the positions [math]\displaystyle{ \mathbf{r_i} }[/math] and momenta [math]\displaystyle{ \mathbf{p_i} }[/math]:

[math]\displaystyle{ \frac{d \mathbf{r_i}}{dt} = \frac{\partial \mathcal{H}}{\partial \mathbf{p_i}}, \qquad \frac{d\mathbf{p_i}}{dt} = -\frac{\partial \mathcal{H}}{\partial \mathbf{r_i}}, }[/math]

where [math]\displaystyle{ \mathcal{H} }[/math] is the Hamiltonian:

[math]\displaystyle{ \mathcal{H} = -\frac{G m_1 m_2}{|\mathbf{r_1} - \mathbf{r_2}|}-\frac{G m_2 m_3}{|\mathbf{r_3} - \mathbf{r_2}|} -\frac{G m_3 m_1}{|\mathbf{r_3} - \mathbf{r_1}|} + \frac{\mathbf{p_1}^2}{2m_1} + \frac{\mathbf{p_2}^2}{2m_2} + \frac{\mathbf{p_3}^2}{2m_3}. }[/math]

In this case [math]\displaystyle{ \mathcal{H} }[/math] is simply the total energy of the system, gravitational plus kinetic.

Restricted three-body problem

The circular restricted three-body problem[clarification needed] is a valid approximation of elliptical orbits found in the Solar System,[citation needed] and this can be visualized as a combination of the potentials due to the gravity of the two primary bodies along with the centrifugal effect from their rotation (Coriolis effects are dynamic and not shown). The Lagrange points can then be seen as the five places where the gradient on the resultant surface is zero, indicating that the forces are in balance there.[citation needed]

In the restricted three-body problem, a body of negligible mass (the "planetoid") moves under the influence of two massive bodies. Having negligible mass, the force that the planetoid exerts on the two massive bodies may be neglected, and the system can be analysed and can therefore be described in terms of a two-body motion.[3][5] With respect to a rotating reference frame, the two co-orbiting bodies are stationary, and the third can be stationary as well at the Lagrangian points, or move around them, for instance on a horseshoe orbit. It can be useful to consider the effective potential. Usually this two-body motion is taken to consist of circular orbits around the center of mass, and the planetoid is assumed to move in the plane defined by the circular orbits.

The restricted three-body problem is easier to analyze theoretically than the full problem. It is of practical interest as well since it accurately describes many real-world problems, the most important example being the Earth–Moon–Sun system. For these reasons, it has occupied an important role in the historical development of the three-body problem.

Mathematically, the problem is stated as follows.[according to whom?] Let [math]\displaystyle{ m_{1,2} }[/math] be the masses of the two massive bodies, with (planar) coordinates [math]\displaystyle{ (x_1, y_1) }[/math] and [math]\displaystyle{ (x_2, y_2) }[/math], and let [math]\displaystyle{ (x, y) }[/math] be the coordinates of the planetoid. For simplicity, choose units such that the distance between the two massive bodies, as well as the gravitational constant, are both equal to [math]\displaystyle{ 1 }[/math]. Then, the motion of the planetoid is given by

[math]\displaystyle{ \begin{align} \frac{d^2 x}{dt^2} = -m_1 \frac{x - x_1}{r_1^3} - m_2 \frac{x - x_2}{r_2^3}, \\ \frac{d^2 y}{dt^2} = -m_1 \frac{y - y_1}{r_1^3} - m_2 \frac{y - y_2}{r_2^3}, \end{align} }[/math]

where [math]\displaystyle{ r_i = \sqrt{(x - x_i)^2 + (y - y_i)^2} }[/math]. In this form the equations of motion carry an explicit time dependence through the coordinates [math]\displaystyle{ x_i(t), y_i(t) }[/math]. However, this time dependence can be removed through a transformation to a rotating reference frame, which simplifies any subsequent analysis.

Solutions

General solution

While a system of 3 bodies interacting gravitationally is chaotic, a system of 3 bodies interacting elastically isn't.

There is no general closed-form solution to the three-body problem,[1] meaning there is no general solution that can be expressed in terms of a finite number of standard mathematical operations. Moreover, the motion of three bodies is generally non-repeating, except in special cases.[6]

However, in 1912 the Finland mathematician Karl Fritiof Sundman proved that there exists an analytic solution to the three-body problem in the form of a Puiseux series, specifically a power series in terms of powers of t1/3.[7] This series converges for all real t, except for initial conditions corresponding to zero angular momentum. In practice, the latter restriction is insignificant since initial conditions with zero angular momentum are rare, having Lebesgue measure zero.

An important issue in proving this result is the fact that the radius of convergence for this series is determined by the distance to the nearest singularity. Therefore, it is necessary to study the possible singularities of the three-body problems. As is briefly discussed below, the only singularities in the three-body problem are binary collisions (collisions between two particles at an instant) and triple collisions (collisions between three particles at an instant).

Collisions, whether binary or triple (in fact, any number), are somewhat improbable, since it has been shown that they correspond to a set of initial conditions of measure zero. However, there is no criterion known to be put on the initial state in order to avoid collisions for the corresponding solution. So Sundman's strategy consisted of the following steps:

  1. Using an appropriate change of variables to continue analyzing the solution beyond the binary collision, in a process known as regularization.
  2. Proving that triple collisions only occur when the angular momentum L vanishes. By restricting the initial data to L ≠ 0, he removed all real singularities from the transformed equations for the three-body problem.
  3. Showing that if L ≠ 0, then not only can there be no triple collision, but the system is strictly bounded away from a triple collision. This implies, by using Cauchy's existence theorem for differential equations, that there are no complex singularities in a strip (depending on the value of L) in the complex plane centered around the real axis (shades of Kovalevskaya).
  4. Find a conformal transformation that maps this strip into the unit disc. For example, if s = t1/3 (the new variable after the regularization) and if |ln s| ≤ β,[clarification needed] then this map is given by [math]\displaystyle{ \sigma = \frac{e^\frac{\pi s}{2\beta} - 1}{e^\frac{\pi s}{2\beta} + 1}. }[/math]

This finishes the proof of Sundman's theorem.

The corresponding series, however, converges very slowly. That is, obtaining a value of meaningful precision requires so many terms that this solution is of little practical use. Indeed, in 1930, David Beloriszky calculated that if Sundman's series were to be used for astronomical observations, then the computations would involve at least 108000000 terms.[8]

Special-case solutions

In 1767, Leonhard Euler found three families of periodic solutions in which the three masses are collinear at each instant. See Euler's three-body problem.

In 1772, Lagrange found a family of solutions in which the three masses form an equilateral triangle at each instant. Together with Euler's collinear solutions, these solutions form the central configurations for the three-body problem. These solutions are valid for any mass ratios, and the masses move on Keplerian ellipses. These four families are the only known solutions for which there are explicit analytic formulae. In the special case of the circular restricted three-body problem, these solutions, viewed in a frame rotating with the primaries, become points referred to as L1, L2, L3, L4, and L5, and called Lagrangian points, with L4 and L5 being symmetric instances of Lagrange's solution.

In work summarized in 1892–1899, Henri Poincaré established the existence of an infinite number of periodic solutions to the restricted three-body problem, together with techniques for continuing these solutions into the general three-body problem.

In 1893, Meissel stated what is now called the Pythagorean three-body problem: three masses in the ratio 3:4:5 are placed at rest at the vertices of a 3:4:5 right triangle. Burrau[9] further investigated this problem in 1913. In 1967 Victor Szebehely and C. Frederick Peters established eventual escape for this problem using numerical integration, while at the same time finding a nearby periodic solution.[10]

An animation of the figure-8 solution to the three-body problem over a single period T ≃ 6.3259.[11]
20 examples of periodic solutions to the three-body problem.

In the 1970s, Michel Hénon and Roger A. Broucke each found a set of solutions that form part of the same family of solutions: the Broucke–Henon–Hadjidemetriou family. In this family the three objects all have the same mass and can exhibit both retrograde and direct forms. In some of Broucke's solutions two of the bodies follow the same path.[12]

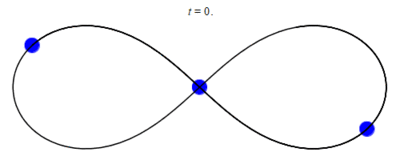
In 1993, a zero angular momentum solution with three equal masses moving around a figure-eight shape was discovered numerically by physicist Cris Moore at the Santa Fe Institute.[13] Its formal existence was later proved in 2000 by mathematicians Alain Chenciner and Richard Montgomery.[14][15] The solution has been shown numerically to be stable for small perturbations of the mass and orbital parameters, which makes it possible that such orbits could be observed in the physical universe. However, it has been argued that this occurrence is unlikely since the domain of stability is small. For instance, the probability of a binary–binary scattering event[clarification needed] resulting in a figure-8 orbit has been estimated to be a small fraction of a percent.[16]

In 2013, physicists Milovan Šuvakov and Veljko Dmitrašinović at the Institute of Physics in Belgrade discovered 13 new families of solutions for the equal-mass zero-angular-momentum three-body problem.[6][12]

In 2015, physicist Ana Hudomal discovered 14 new families of solutions for the equal-mass zero-angular-momentum three-body problem.[17]

In 2017, researchers Xiaoming Li and Shijun Liao found 669 new periodic orbits of the equal-mass zero-angular-momentum three-body problem.[18] This was followed in 2018 by an additional 1223 new solutions for a zero-angular-momentum system of unequal masses.[19]

In 2018, Li and Liao reported 234 solutions to the unequal-mass "free-fall" three-body problem.[20] The free fall formulation of the three body problem starts with all three bodies at rest. Because of this, the masses in a free-fall configuration do not orbit in a closed "loop", but travel forward and backward along an open "track".

In 2023, Ivan Hristov, Radoslava Hristova, Dmitrašinović and Kiyotaka Tanikawa published a search for "periodic free-fall orbits" three-body problem, limited to the equal-mass case, in which they found 12,409 distinct solutions.[21]

Numerical approaches

Using a computer, the problem may be solved to arbitrarily high precision using numerical integration although high precision requires a large amount of CPU time. There have been attempts of creating computer programs that numerically solve the three-body problem (and by extension, the n-body problem) involving both electromagnetic and gravitational interactions, and incorporating modern theories of physics such as special relativity.[22] In addition, using the theory of random walks, an approximate probability of different outcomes may be computed.[23][24]

History

The gravitational problem of three bodies in its traditional sense dates in substance from 1687, when Isaac Newton published his Philosophiæ Naturalis Principia Mathematica, when Newton was trying to figure out if any long term stability is possible, especially the system of our Earth, the Moon, and the Sun. He was guided under the major Renaissance astronomers Nicolaus Copernicus, Tycho Brahe and Johannes Kepler to the beginning of the gravitational three-body problem.[25] In Proposition 66 of Book 1 of the Principia, and its 22 Corollaries, Newton took the first steps in the definition and study of the problem of the movements of three massive bodies subject to their mutually perturbing gravitational attractions. In Propositions 25 to 35 of Book 3, Newton also took the first steps in applying his results of Proposition 66 to the lunar theory, the motion of the Moon under the gravitational influence of Earth and the Sun.[26] Later, this problem was also applied to other planets' interactions with the Earth and the Sun.[25]

The physical problem was first addressed by Amerigo Vespucci and subsequently by Galileo Galilei, as well as Simon Stevin, but they did not realize what they contributed. Though Galileo determined that the speed of fall of all bodies changes uniformly and in the same way, he did not apply it to planetary motions.[25] Whereas in 1499, Vespucci used knowledge of the position of the Moon to determine his position in Brazil.[27] It became of technical importance in the 1720s, as an accurate solution would be applicable to navigation, specifically for the determination of longitude at sea, solved in practice by John Harrison's invention of the marine chronometer. However the accuracy of the lunar theory was low, due to the perturbing effect of the Sun and planets on the motion of the Moon around Earth.

Jean le Rond d'Alembert and Alexis Clairaut, who developed a longstanding rivalry, both attempted to analyze the problem in some degree of generality; they submitted their competing first analyses to the Académie Royale des Sciences in 1747.[28] It was in connection with their research, in Paris during the 1740s, that the name "three-body problem" (French: Problème des trois Corps) began to be commonly used. An account published in 1761 by Jean le Rond d'Alembert indicates that the name was first used in 1747.[29]

From the end of the 19th century to early 20th century, the approach to solve the three-body problem with the usage of short-range attractive two-body forces was developed by scientists, which offered P.F. Bedaque, H.-W. Hammer and U. van Kolck an idea to renormalize the short-range three-body problem, providing scientists a rare example of a renormalization group limit cycle at the beginning of the 21st century.[30] George William Hill worked on the restricted problem in the late 19th century with an application of motion of Venus and Mercury.[31]

At the beginning of the 20th century, Karl Sundman approached the problem mathematically and systematically by providing a function theoretical proof to the problem valid for all values of time. It was the first time scientists theoretically solved three-body problem. However, because there was not enough qualitative solution of this system, and it was too slow for scientists to practically apply it, this solution still left some issues unresolved.[32] In the 1970s, implication to three-body from two-body forces had been discovered by V. Efimov, which was named as Efimov Effect.[33]

In 2017, Shijun Liao and Xiaoming Li applied a new strategy of numerical simulation for chaotic systems called the clean numerical simulation (CNS), with the use of a national supercomputer, to successfully gain 695 families of periodic solutions of the three-body system with equal mass.[34]

In 2019, Breen et al. announced a fast neural network solver for the three-body problem, trained using a numerical integrator.[35]

In September 2023, several possible solutions have been found to the problem according to reports.[36][37]

Other problems involving three bodies

The term "three-body problem" is sometimes used in the more general sense to refer to any physical problem involving the interaction of three bodies.

A quantum-mechanical analogue of the gravitational three-body problem in classical mechanics is the helium atom, in which a helium nucleus and two electrons interact according to the inverse-square Coulomb interaction. Like the gravitational three-body problem, the helium atom cannot be solved exactly.[38]

In both classical and quantum mechanics, however, there exist nontrivial interaction laws besides the inverse-square force that do lead to exact analytic three-body solutions. One such model consists of a combination of harmonic attraction and a repulsive inverse-cube force.[39] This model is considered nontrivial since it is associated with a set of nonlinear differential equations containing singularities (compared with, e.g., harmonic interactions alone, which lead to an easily solved system of linear differential equations). In these two respects it is analogous to (insoluble) models having Coulomb interactions, and as a result has been suggested as a tool for intuitively understanding physical systems like the helium atom.[39][40]

Within the point vortex model, the motion of vortices in a two-dimensional ideal fluid is described by equations of motion that contain only first-order time derivatives. I.e. in contrast to Newtonian mechanics, it is the velocity and not the acceleration that is determined by their relative positions. As a consequence, the three-vortex problem is still integrable,[41] while at least four vortices are required to obtain chaotic behavior.[42] One can draw parallels between the motion of a passive tracer particle in the velocity field of three vortices and the restricted three-body problem of Newtonian mechanics.[43]

The gravitational three-body problem has also been studied using general relativity. Physically, a relativistic treatment becomes necessary in systems with very strong gravitational fields, such as near the event horizon of a black hole. However, the relativistic problem is considerably more difficult than in Newtonian mechanics, and sophisticated numerical techniques are required. Even the full two-body problem (i.e. for arbitrary ratio of masses) does not have a rigorous analytic solution in general relativity.[44]

n-body problem

The three-body problem is a special case of the n-body problem, which describes how n objects move under one of the physical forces, such as gravity. These problems have a global analytical solution in the form of a convergent power series, as was proven by Karl F. Sundman for n = 3 and by Qiudong Wang for n > 3 (see n-body problem for details). However, the Sundman and Wang series converge so slowly that they are useless for practical purposes;[45] therefore, it is currently necessary to approximate solutions by numerical analysis in the form of numerical integration or, for some cases, classical trigonometric series approximations (see n-body simulation). Atomic systems, e.g. atoms, ions, and molecules, can be treated in terms of the quantum n-body problem. Among classical physical systems, the n-body problem usually refers to a galaxy or to a cluster of galaxies; planetary systems, such as stars, planets, and their satellites, can also be treated as n-body systems. Some applications are conveniently treated by perturbation theory, in which the system is considered as a two-body problem plus additional forces causing deviations from a hypothetical unperturbed two-body trajectory.

See also


References

  1. ↑ 1.0 1.1 1.2 Barrow-Green, June (2008). "The Three-Body Problem". The Princeton Companion to Mathematics. Princeton University Press. pp. 726–728. 
  2. ↑ "Historical Notes: Three-Body Problem". http://www.wolframscience.com/reference/notes/972d. 
  3. ↑ 3.0 3.1 Barrow-Green, June (1997). Poincaré and the Three Body Problem. American Mathematical Society. pp. 8–12. ISBN 978-0-8218-0367-7. Bibcode: 1997ptbp.book.....B. 
  4. ↑ "The Three-Body Problem". http://www.phys.lsu.edu/faculty/gonzalez/Teaching/Phys7221/ThreeBodyProblem.pdf. 
  5. ↑ Restricted Three-Body Problem, Science World.
  6. ↑ 6.0 6.1 Cartwright, Jon (8 March 2013). "Physicists Discover a Whopping 13 New Solutions to Three-Body Problem". Science Now. https://www.science.org/content/article/physicists-discover-whopping-13-new-solutions-three-body-problem. Retrieved 2013-04-04. 
  7. ↑ Barrow-Green, J. (2010). The dramatic episode of Sundman, Historia Mathematica 37, pp. 164–203.
  8. ↑ Beloriszky, D. (1930). "Application pratique des méthodes de M. Sundman à un cas particulier du problème des trois corps". Bulletin Astronomique. Série 2 6: 417–434. Bibcode: 1930BuAst...6..417B. 
  9. ↑ Burrau (1913). "Numerische Berechnung eines Spezialfalles des Dreikörperproblems". Astronomische Nachrichten 195 (6): 113–118. doi:10.1002/asna.19131950602. Bibcode: 1913AN....195..113B. https://zenodo.org/record/1424886. 
  10. ↑ Victor Szebehely; C. Frederick Peters (1967). "Complete Solution of a General Problem of Three Bodies". Astronomical Journal 72: 876. doi:10.1086/110355. Bibcode: 1967AJ.....72..876S. 
  11. ↑ Here the gravitational constant G has been set to 1, and the initial conditions are r1(0) = -r3(0) = (-0.97000436, 0.24308753); r2(0) = (0,0); v1(0) = v3(0) = (0.4662036850, 0.4323657300); v2(0) = (-0.93240737, -0.86473146). The values are obtained from Chenciner & Montgomery (2000).
  12. ↑ 12.0 12.1 "Three-body Gallery". http://suki.ipb.ac.rs/3body/. 
  13. ↑ Moore, Cristopher (1993). "Braids in classical dynamics". Physical Review Letters 70 (24): 3675–3679. doi:10.1103/PhysRevLett.70.3675. PMID 10053934. Bibcode: 1993PhRvL..70.3675M. http://tuvalu.santafe.edu/~moore/braids-prl.pdf. Retrieved 2016-01-01. 
  14. ↑ Chenciner, Alain; Montgomery, Richard (2000). "A remarkable periodic solution of the three-body problem in the case of equal masses". Annals of Mathematics. Second Series 152 (3): 881–902. doi:10.2307/2661357. Bibcode: 2000math.....11268C. 
  15. ↑ Montgomery, Richard (2001). "A new solution to the three-body problem". Notices of the American Mathematical Society 48: 471–481. https://www.ams.org/notices/200105/fea-montgomery.pdf. 
  16. ↑ Heggie, Douglas C. (2000). "A new outcome of binary–binary scattering". Monthly Notices of the Royal Astronomical Society 318 (4): L61–L63. doi:10.1046/j.1365-8711.2000.04027.x. Bibcode: 2000MNRAS.318L..61H. 
  17. ↑ Hudomal, Ana (October 2015). "New periodic solutions to the three-body problem and gravitational waves". Master of Science Thesis at the Faculty of Physics, Belgrade University. http://www.scl.rs/theses/msc_ahudomal.pdf. Retrieved 5 February 2019. 
  18. ↑ Li, Xiaoming; Liao, Shijun (December 2017). "More than six hundreds new families of Newtonian periodic planar collisionless three-body orbits". Science China Physics, Mechanics & Astronomy 60 (12): 129511. doi:10.1007/s11433-017-9078-5. ISSN 1674-7348. Bibcode: 2017SCPMA..60l9511L. 
  19. ↑ Li, Xiaoming; Jing, Yipeng; Liao, Shijun (August 2018). "The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum". Publications of the Astronomical Society of Japan 70 (4). doi:10.1093/pasj/psy057. 
  20. ↑ Li, Xiaoming; Liao, Shijun (2019). "Collisionless periodic orbits in the free-fall three-body problem". New Astronomy 70: 22–26. doi:10.1016/j.newast.2019.01.003. Bibcode: 2019NewA...70...22L. 
  21. ↑ Hristov, Ivan; Hristova, Radoslava; Dmitrašinović, Veljko; Tanikawa, Kiyotaka (2023). "Three-body periodic collisionless equal-mass free-fall orbits revisited". arXiv:2308.16159 [physics.class-ph].
  22. ↑ "3body simulator" (in en). https://3body.hk/. 
  23. ↑ Technion (6 October 2021). "A Centuries-Old Physics Mystery? Solved". SciTechDaily (SciTech). https://scitechdaily.com/a-centuries-old-physics-mystery-solved/. 
  24. ↑ Ginat, Yonadav Barry; Perets, Hagai B. (23 July 2021). "Analytical, Statistical Approximate Solution of Dissipative and Nondissipative Binary-Single Stellar Encounters". Physical Review 11 (3): 031020. doi:10.1103/PhysRevX.11.031020. Bibcode: 2021PhRvX..11c1020G. https://journals.aps.org/prx/abstract/10.1103/PhysRevX.11.031020. Retrieved 12 October 2021. 
  25. ↑ 25.0 25.1 25.2 Valtonen, Mauri (3 May 2016). The Three-body Problem from Pythagoras to Hawking. Springer. ISBN 978-3-319-22726-9. OCLC 1171227640. 
  26. ↑ Newton, Isaac (1726). Philosophiæ naturalis principia mathematica. London: G. & J. Innys. doi:10.14711/spcol/b706487. https://lbezone.hkust.edu.hk/bib/b706487. Retrieved 2022-10-05. 
  27. ↑ "Amerigo Vespucci" (in en-us). 23 June 2021. https://www.biography.com/explorer/amerigo-vespucci. 
  28. ↑ The 1747 memoirs of both parties can be read in the volume of Histoires (including Mémoires) of the Académie Royale des Sciences for 1745 (belatedly published in Paris in 1749) (in French):
    Clairaut: "On the System of the World, according to the principles of Universal Gravitation" (at pp. 329–364); and
    d'Alembert: "General method for determining the orbits and the movements of all the planets, taking into account their mutual actions" (at pp. 365–390).The peculiar dating is explained by a note printed on page 390 of the "Memoirs" section: "Even though the preceding memoirs, of Messrs. Clairaut and d'Alembert, were only read during the course of 1747, it was judged appropriate to publish them in the volume for this year" (i.e. the volume otherwise dedicated to the proceedings of 1745, but published in 1749).
  29. ↑ Jean le Rond d'Alembert, in a paper of 1761 reviewing the mathematical history of the problem, mentions that Euler had given a method for integrating a certain differential equation "in 1740 (seven years before there was question of the Problem of Three Bodies)": see d'Alembert, "Opuscules Mathématiques", vol. 2, Paris 1761, Quatorzième Mémoire ("Réflexions sur le Problème des trois Corps, avec de Nouvelles Tables de la Lune ...") pp. 329–312, at sec. VI, p. 245.
  30. ↑ Mohr, R.F.; Furnstahl, R.J.; Hammer, H.-W.; Perry, R.J.; Wilson, K.G. (January 2006). "Precise numerical results for limit cycles in the quantum three-body problem". Annals of Physics 321 (1): 225–259. doi:10.1016/j.aop.2005.10.002. ISSN 0003-4916. Bibcode: 2006AnPhy.321..225M. 
  31. ↑ "Coplanar Motion of Two Planets, One Having a Zero Mass". Annals of Mathematics, Vol. III, pp. 65–73, 1887.
  32. ↑ Barrow-Green, June (1996-10-29). Poincaré and the Three Body Problem. History of Mathematics. 11. Providence, Rhode Island: American Mathematical Society. doi:10.1090/hmath/011. ISBN 978-0-8218-0367-7. http://oro.open.ac.uk/57403/1/335423.pdf. 
  33. ↑ Efimov, V. (1970-12-21). "Energy levels arising from resonant two-body forces in a three-body system" (in en). Physics Letters B 33 (8): 563–564. doi:10.1016/0370-2693(70)90349-7. ISSN 0370-2693. Bibcode: 1970PhLB...33..563E. 
  34. ↑ Liao, Shijun; Li, Xiaoming (2019-11-01). "On the periodic solutions of the three-body problem" (in en). National Science Review 6 (6): 1070–1071. doi:10.1093/nsr/nwz102. ISSN 2095-5138. PMID 34691975. PMC 8291409. https://academic.oup.com/nsr/article/6/6/1070/5537324. 
  35. ↑ Breen, Philip G.; Foley, Christopher N.; Boekholt, Tjarda; Portegies Zwart, Simon (2020). "Newton versus the machine: Solving the chaotic three-body problem using deep neural networks". Monthly Notices of the Royal Astronomical Society 494 (2): 2465–2470. doi:10.1093/mnras/staa713. 
  36. ↑ Watson, Claire (23 September 2023). "We Just Got 12,000 New Solutions to The Infamous Three-Body Problem". ScienceAlert. Archived from the original on 24 September 2023. https://archive.today/20230924005541/https://www.sciencealert.com/we-just-got-12000-new-solutions-to-the-infamous-three-body-problem. Retrieved 23 September 2023. 
  37. ↑ Hristov, Ivan; Hristova, Radoslava; Dmitrašinović, Veljko; Tanikawa, Kiyotaka (31 August 2023). "Three-body periodic collisionless equal-mass free-fall orbits revisited". arXiv:2308.16159 [physics.class-ph].
  38. ↑ Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. p. 311. ISBN 978-0-13-111892-8. OCLC 40251748. 
  39. ↑ 39.0 39.1 Crandall, R.; Whitnell, R.; Bettega, R. (1984). "Exactly soluble two-electron atomic model". American Journal of Physics 52 (5): 438–442. doi:10.1119/1.13650. Bibcode: 1984AmJPh..52..438C. 
  40. ↑ Calogero, F. (1969). "Solution of a Three-Body Problem in One Dimension". Journal of Mathematical Physics 10 (12): 2191–2196. doi:10.1063/1.1664820. Bibcode: 1969JMP....10.2191C. 
  41. ↑ Aref, Hassan (1979-03-01). "Motion of three vortices". The Physics of Fluids 22 (3): 393–400. doi:10.1063/1.862605. ISSN 0031-9171. Bibcode: 1979PhFl...22..393A. https://aip.scitation.org/doi/10.1063/1.862605. 
  42. ↑ Aref, Hassan; Pomphrey, Neil (1980-08-18). "Integrable and chaotic motions of four vortices" (in en). Physics Letters A 78 (4): 297–300. doi:10.1016/0375-9601(80)90375-8. ISSN 0375-9601. Bibcode: 1980PhLA...78..297A. 
  43. ↑ Neufeld, Z; Tél, T (1997-03-21). "The vortex dynamics analogue of the restricted three-body problem: advection in the field of three identical point vortices". Journal of Physics A: Mathematical and General 30 (6): 2263–2280. doi:10.1088/0305-4470/30/6/043. ISSN 0305-4470. Bibcode: 1997JPhA...30.2263N. https://iopscience.iop.org/article/10.1088/0305-4470/30/6/043. 
  44. ↑ Musielak, Z. E.; Quarles, B. (2014). "The three-body problem". Reports on Progress in Physics 77 (6): 065901. doi:10.1088/0034-4885/77/6/065901. ISSN 0034-4885. PMID 24913140. Bibcode: 2014RPPh...77f5901M. 
  45. ↑ Florin Diacu. "The Solution of the n-body Problem", The Mathematical Intelligencer, 1996.

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Three-body_problem&oldid=3284188"