Physics:Spacetime triangle diagram technique

From HandWiki

In physics and mathematics, the spacetime triangle diagram (STTD) technique, also known as the Smirnov method of incomplete separation of variables, is the direct space-time domain method for electromagnetic and scalar wave motion.

Basic stages

  1. (Electromagnetics) The system of Maxwell's equations is reduced to a second-order PDE for the field components, or potentials, or their derivatives.
  2. The spatial variables are separated using convenient expansions into series and/or integral transforms—except one that remains bounded with the time variable, resulting in a PDE of hyperbolic type.
  3. The resulting hyperbolic PDE and the simultaneously transformed initial conditions compose a problem, which is solved using the Riemann–Volterra integral formula. This yields the generic solution expressed via a double integral over a triangle domain in the bounded-coordinate—time space. Then this domain is replaced by a more complicated but smaller one, in which the integrant is essentially nonzero, found using a strictly formalized procedure involving specific spacetime triangle diagrams (see, e.g., Refs.[1][2][3]).
  4. In the majority of cases the obtained solutions, being multiplied by known functions of the previously separated variables, result in the expressions of a clear physical meaning (nonsteady-state modes). In many cases, however, more explicit solutions can be found summing up the expansions or doing the inverse integral transform.

STTD versus Green's function technique

The STTD technique belongs to the second among the two principal ansätze for theoretical treatment of waves — the frequency domain and the direct spacetime domain. The most well-established method for the inhomogeneous (source-related) descriptive equations of wave motion is one based on the Green's function technique.[4] For the circumstances described in Section 6.4 and Chapter 14 of Jackson's Classical Electrodynamics,[4] it can be reduced to calculation of the wave field via retarded potentials (in particular, the Liénard–Wiechert potentials).

Despite certain similarity between Green's and Riemann–Volterra methods (in some literature the Riemann function is called the Riemann–Green function [5]), their application to the problems of wave motion results in distinct situations:

  • The definitions of both Green's function and corresponding Green's solution are not unique as they leave room for addition of arbitrary solution of the homogeneous equation; in some circumstances the particular choice of Green's function and the final solution are defined by boundary condition(s) or plausibility and physical admissibility of the constructed wavefunctions.[6] The Riemann function is a solution of the homogeneous equation that additionally must take a certain value at the characteristics and thus is defined in a unique way.
  • In contrast to Green's method that provides a particular solution of the inhomogeneous equation, the Riemann–Volterra method is related to the corresponding problem, comprising the PDE and initial conditions,

[7] [8] and it was the Riemann–Volterra representation that Smirnov used in his Course of Higher Mathematics to prove the uniqueness of the solution to the above problem (see,[8] item 143).

  • In the general case, Green's formula implies integration over the entire domain of variation of coordinates and time, while integration in the Riemann–Volterra solution is carried out within a limited triangle region, assuring the boundness of the solution support.
  • Causality of the (unique) Riemann–Volterra solution is provided automatically, without need to recur to additional considerations, such as the retarded nature of the argument, wave propagation in certain direction, specific choice of the integration path, etc. (Usually the descriptive equations, such as the classical scalar wave equation, possess the T-symmetry. It is the time-asymmetric initial conditions that define the arrow of time through the limitation of the integration domain in the Riemann formula to [math]\displaystyle{ t \gt 0 }[/math], see more in[2] and a particular example given below.)
  • Green's function can be readily derived from the Liénard–Wiechert potential of a moving point source, but concrete calculation of the wavefunction, inevitably involving the analysis of the retarded argument, may develop in a rather complicated task unless some special techniques, like the parametric method,[9]

are invoked. The Riemann-Volterra approach presents the same or even more serious difficulties, especially when one deals with the bounded-support sources: here the actual limits of integration must be defined from the system of inequalities involving the space-time variables and parameters of the source term. However, this definition can be strictly formalized using the spacetime triangle diagrams. Playing the same role as the Feynman diagrams in particle physics, STTDs provide a strict and illustrative procedure for definition of areas with the same analytic representation of the integration domain in the 2D space spanned by the non-separated spatial variable and time.

Drawbacks of the method

  • The method can only be applied to problems possessing known Riemann function.
  • Application of the method and analysis of the results obtained require more profound knowledge of the special functions of mathematical physics (e.g., operating with the generalized functions, Mathieu functions of different kinds and Lommel's functions of two variables) than Green's function method.
  • In some cases the final integrals require special consideration in the domains of rapid oscillation of the Riemann function.

Most important concretizations

General considerations

Several efficient methods for scalarizing electromagnetic problems in the orthogonal coordinates [math]\displaystyle{ x_1, x_2, x_3 }[/math] were discussed by Borisov in Ref.[10] The most important conditions of their applicability are [math]\displaystyle{ h_3 = 1 }[/math] and [math]\displaystyle{ \partial_3(h_1/h_2) = 0 }[/math], where [math]\displaystyle{ h_i, i= 1,2,3 }[/math] are the metric (Lamé) coefficients (so that the squared length element is [math]\displaystyle{ ds^2 = h_1^2 dx_1^2+h_2^2 dx_2^2+h_3^2 dx_3^2 }[/math]). Remarkably, this condition is met for the majority of practically important coordinate systems, including the Cartesian, general-type cylindrical and spherical ones.

For the problems of wave motion is free space, the basic method of separating spatial variables is the application of integral transforms, while for the problems of wave generation and propagation in the guiding systems the variables are usually separated using expansions in terms of the basic functions (modes) meeting the required boundary conditions at the surface of the guiding system.

Cartesian and cylindrical coordinates

In the Cartesian [math]\displaystyle{ \left\{ x_1=x, \; x_2=y, \; x_3=z \right\} }[/math] and general-type cylindrical coordinates [math]\displaystyle{ \left\{ x_1=x_1(x,y), \; x_2=x_2(x,y), \; x_3=z \right\} }[/math] separation of the spatial variables result in the initial value problem for a hyperbolic PDE known as the 1D Klein–Gordon equation (KGE)

[math]\displaystyle{ \begin{align} & \left( \partial_\tau ^2 - \partial_z^2 + k^2 \right)\psi(\tau,z) = f(\tau,z) \\ & \psi (\tau ,z) = 0 \text{ for } \tau \lt 0 \end{align} }[/math]

Here [math]\displaystyle{ \tau }[/math] is the time variable expressed in units of length using some characteristic velocity (e.g., speed of light or sound), [math]\displaystyle{ k }[/math] is a constant originated from the separation of variables, and [math]\displaystyle{ f(\tau ,z) }[/math] represents a part of the source term in the initial wave equation that remains after application of the variable-separation procedures (a series coefficient or a result of an integral transform).

The above problem possesses known Riemann function

[math]\displaystyle{ R_k(\tau ,z;\tau ',z') = J_0\left( k\sqrt {(\tau - \tau')^2 - (z - z')^2} \right), }[/math]

where [math]\displaystyle{ J_0(\cdot) }[/math] is the Bessel function of the first kind of order zero.

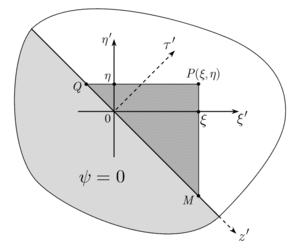
Canonical variables
Canonical variables ξ, η.
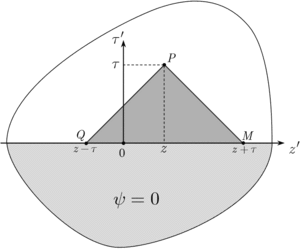
Initial variables
Initial variables z, τ.
The simplest STTD representing a triangle integration domain resulted from the Riemann–Volterra integral formula.

Passing to the canonical variables [math]\displaystyle{ z, \tau \to \xi, \eta }[/math] one gets the simplest STTD diagram reflecting straightforward application of the Riemann–Volterra method,[7][8] with the fundamental integration domain represented by spacetime triangle MPQ (in dark grey).

Rotation of the STTD 45° counter clockwise yields more common form of the STTD in the conventional spacetime [math]\displaystyle{ z, \tau }[/math].

For the homogeneous initial conditions the (unique[8]) solution of the problem is given by the Riemann formula

[math]\displaystyle{ \psi(\tau ,z) = \frac{1}{2} \iint\limits_{\triangle MPQ} \, d\tau' \, dz'R(\tau ,z;\tau',z')f(\tau',z'). }[/math]

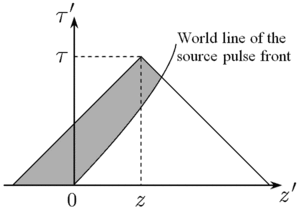
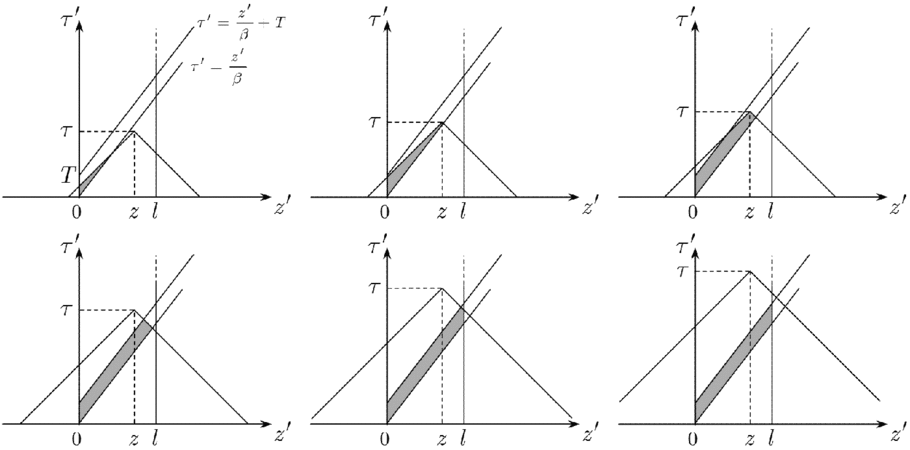
Evolution of the wave process can be traced using a fixed observation point ([math]\displaystyle{ z = \text{const} }[/math]) successively increasing the triangle height ([math]\displaystyle{ \tau }[/math]) or, alternatively, taking "momentary picture" of the wavefunction [math]\displaystyle{ \psi }[/math] by shifting the spacetime triangle along the [math]\displaystyle{ z }[/math] axis ([math]\displaystyle{ \tau = \text{const} }[/math]).

More useful and sophisticated STTDs correspond to pulsed sources whose support is limited in spacetime. Each limitation produce specific modifications in the STTD, resulting to smaller and more complicated integration domains in which the integrand is essentially non-zero. Examples of most common modifications and their combined actions are illustrated below.

Static limitations to the source area[10]
STTD for a source limited from left by plane [math]\displaystyle{ z = 0 }[/math], i.e. [math]\displaystyle{ f(\tau ,z) = 0 \text{ for } z \lt 0 }[/math], which is the case, e.g., for a travelling source propagating along a semi-infinite radiator [math]\displaystyle{ l }[/math].
STTD for a source limited from right by plane [math]\displaystyle{ z = l }[/math], i.e. [math]\displaystyle{ f(\tau,z) = 0 \text{ for } z \gt l. }[/math]
STTD for a source limited from both sides, i.e. [math]\displaystyle{ f(\tau ,z) = 0 \text{ for } z \notin [0,l] }[/math], which is the case, e.g., for a travelling source propagating along a radiator of finite length [math]\displaystyle{ l }[/math].
Combined action of limitations of different type, see Refs.[1][10][11][12][13] for details and more complicated examples
STTD for a semi-infinite travelling source pulse.
STTD for a finite travelling source pulse.
STTD for a finite travelling source pulse propagating along a semi-infinite radiator [math]\displaystyle{ z \isin \left[ 0, \infty \right) }[/math].
A sequence of generic STTDs for a "short", finite source pulse of duration [math]\displaystyle{ T }[/math] propagating along a finite radiator [math]\displaystyle{ z \isin [0,l] }[/math] with a constant velocity [math]\displaystyle{ \beta }[/math].[citation needed] In this case the source can be expressed in the form
[math]\displaystyle{ f(\tau,z) = f_0(\tau,z) \times h(z) h(l - z) h \left( \tau - \frac{z}{\beta} \right) h \left( T - \tau + \frac{z}{\beta} \right), }[/math]
    where [math]\displaystyle{ h ( \cdot ) }[/math] is the Heaviside step function.
The same STTD sequence for a "long" pulse.[citation needed]

Spherical coordinates

In the spherical coordinate system — which in view of the General considerations must be represented in the sequence [math]\displaystyle{ \left\{x_1=\theta, \; x_2=\varphi, \; x_3=r \right\} }[/math], assuring [math]\displaystyle{ h_3 = 1 }[/math] — one can scalarize problems for the transverse electric (TE) or transverse magnetic (TM) waves using the Borgnis functions, Debye potentials or Hertz vectors. Subsequent separation of the angular variables [math]\displaystyle{ \theta, \varphi }[/math] via expansion of the initial wavefunction [math]\displaystyle{ \psi \left( \tau, \theta, \varphi, r \right) }[/math] and the source

[math]\displaystyle{ \; f\left( \tau, \theta, \varphi, r \right) }[/math] in terms of
[math]\displaystyle{ \left( \begin{array}{c} \sin m\varphi \\ \cos m\varphi \end{array} \right) P_n^{(m)}(\cos \theta), }[/math]

where [math]\displaystyle{ P_n^{(m)} \! \left( \cdot \right) }[/math] is the associated Legendre polynomial of degree [math]\displaystyle{ n }[/math] and order [math]\displaystyle{ m }[/math], results in the initial value problem for the hyperbolic Euler–Poisson–Darboux equation[3][10]

[math]\displaystyle{ \begin{align} & \left( \partial _\tau ^2 - \partial _r^2 + \frac{n(n + 1)}{r^2} \right)\psi_{nm}(\tau,r) = f_{nm}(\tau, r) \\ & \psi _{nm}(\tau,r) = 0 \text{ for } \tau \lt 0 \end{align} }[/math]

known to have the Riemann function

[math]\displaystyle{ R(\tau,r;\tau',r') = {P_n}\left( \frac{r^2 + {r'}^2 - (\tau - \tau')^2}{2rr'} \right), }[/math]

where [math]\displaystyle{ P_n \! \left( \cdot \right) }[/math] is the (ordinary) Legendre polynomial of degree [math]\displaystyle{ n }[/math].

Equivalence of the STTD (Riemann) and Green's function solutions

The STTD technique represents an alternative to the classical Green's function method. Due to uniqueness of the solution to the initial value problem in question,[8] in the particular case of zero initial conditions the Riemann solution provided by the STTD technique must coincide with the convolution of the causal Green's function and the source term.

The two methods provide apparently different descriptions of the wavefunction: e.g., the Riemann function to the Klein–Gordon problem is a Bessel function (which must be integrated, together with the source term, over the restricted area represented by the fundamental triangle MPQ) while the retarded Green's function to the Klein–Gordon equation is a Fourier transform of the imaginary exponential term (to be integrated over the entire plane [math]\displaystyle{ z',\tau' }[/math], see, for example, Sec. 3.1. of Ref.[14] ) reducible to

[math]\displaystyle{ G_k(\tau,z;\tau',z') = - \frac{1}{(2\pi)^2} \int\limits_{-\infty}^\infty dp \, {\rm e}^{ip(z - z')} \int\limits_{-\infty}^\infty d\Omega \, \frac{{\rm e}^{i\Omega(\tau -\tau')}}{\Omega^2 - p^2 - k^2}. }[/math]

Extending integration with respect to [math]\displaystyle{ \Omega }[/math] to the complex domain, using the residue theorem (with the poles [math]\displaystyle{ \Omega_{1,2} }[/math] chosen as [math]\displaystyle{ \lim_{\varepsilon \to 0+} \left(\pm \sqrt {p^2 + k^2 + i\varepsilon} \right) }[/math] to satisfy the causality conditions) one gets

[math]\displaystyle{ G_k(\tau,z;\tau',z') = \frac{1}{\pi} \int\limits_0^\infty dp \, \frac{{\sin \left((\tau - \tau')\sqrt {p^2 + k^2} \right)}}{\sqrt {p^2 + k^2}} \cos(p(z - z')). }[/math]

Using formula 3.876-1 of Gradshteyn and Ryzhik,[15]

[math]\displaystyle{ \int\limits_0^\infty dx \, \frac{\sin(p\sqrt {x^2 + a^2})}{\sqrt {x^2 + a^2}} \cos(bx) = \left\{ \begin{align} & \frac{\pi}{2} J_0(a\sqrt {p^2 - b^2}) & \text{ for } & 0 \lt b \lt p \\ & 0 & \text{ for } & b \gt p \gt 0 \end{align} \right. \qquad (a\gt 0), }[/math]

the last Green's function representation reduces to the expression[16]

[math]\displaystyle{ \frac{1}{2} J_0\left( k\sqrt {(\tau - \tau ')^2 - (z - z')^2} \right) h(\tau - \tau ' - |z - z'|), }[/math]

in which 1/2 is the scaling factor of the Riemann formula and [math]\displaystyle{ J_0(\cdot) }[/math] the Riemann function, while the Heaviside step function [math]\displaystyle{ h(\cdot) }[/math] reduces, for [math]\displaystyle{ \tau \gt 0 }[/math], the area of integration to the fundamental triangle MPQ, making the Green's function solution equal to that provided by the STTD technique.

References and notes

  1. ↑ 1.0 1.1 A.B. Utkin, Localized Waves Emanated by Pulsed Sources: The Riemann–Volterra Approach. In: Hugo E. Hernández-Figueroa, Erasmo Recami, and Michel Zamboni-Rached (eds.) Non-diffracting Waves. Wiley-VCH: Berlin, ISBN:978-3-527-41195-5, pp. 287–306 (2013)
  2. ↑ 2.0 2.1 A.B. Utkin, The Riemann–Volterra time-domain technique for waveguides: A case study for elliptic geometry. Wave Motion 49(2), 347–363 (2012), doi: 10.1016/j.wavemoti.2011.12.001
  3. ↑ 3.0 3.1 V.V. Borisov, A.V. Manankova, A.B. Utkin, Spherical harmonic representation of the electromagnetic field produced by a moving pulse of current density, Journal of Physics A: Mathematical and General 29(15), 4493–4514 (1996), doi: 10.1088/0305-4470/29/15/020
  4. ↑ 4.0 4.1 J. D. Jackson, Classical Electrodynamics, 3rd ed., Wiley, New York (1999)
  5. ↑ see, e.g., G. A. Korn and T. M. Korn, Mathematical Handbook for Scientists and Engineers, Courier Dover Publications, New York (2000)
  6. ↑ A comprehensive discussion of this subject can found in H. Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 5th ed., World Scientific, Singapore (2009)
  7. ↑ 7.0 7.1 R. Courant and D. Hilbert, Methods of Mathematical Physics, Vol. 2, Wiley, New York (1989)
  8. ↑ 8.0 8.1 8.2 8.3 8.4 V.I. Smirnov, A Course of Higher Mathematics, Vol. 4: Integral Equations and Partial Differential Equations, Pergamon Press, Oxford (1964)
  9. ↑ C.J. Chapman, The spiral Green function in acoustics and electromagnetism, Proc. Roy. Soc. A 431(1881), 157–167 (1990), doi: 10.1098/rspa.1990.0124
  10. ↑ 10.0 10.1 10.2 10.3 V.V. Borisov, Electromagnetic Fields of Transient Currents. Leningrad State University Press: Leningrad (1996, in Russian)
  11. ↑ V.V. Borisov and A.B. Utkin, The transient electromagnetic field produced by a moving pulse of line current, Journal of Physics D: Applied Physics 28(4), 614-622 (1995), doi: 10.1088/0022-3727/28/4/003
  12. ↑ A.B. Utkin, Droplet-shaped waves: casual finite-support analogs of X-shaped waves, J. Opt. Soc. Am. A 29(4), 457-462 (2012), doi: 10.1364/JOSAA.29.000457
  13. ↑ A.B. Utkin, Droplet-shape wave produced by line macroscopic current pulse of finite length, IEEE Xplore DD-2013, ISBN:978-1-4799-1037-3, 145–150 (2013), doi: 10.1109/DD.2013.6712820
  14. ↑ W. Geyi, A time-domain theory of waveguide, Progress in Electromagnetics Research 59, 267–297 (2006), doi: 10.2528/PIER05102102
  15. ↑ "3.876." (in English). Table of Integrals, Series, and Products (8th ed.). Academic Press, Inc.. 2015. p. 486. ISBN 978-0-12-384933-5. 
  16. ↑ Apparently this result was first published by Geyi (2006: 275), merely as a way to simplify the Green's solution and reduce the domain of integration.



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Spacetime_triangle_diagram_technique&oldid=2932836"