Physics:Two-dimensional electronic spectroscopy

From HandWiki

Two-dimensional electronic spectroscopy (2DES) is an ultrafast laser spectroscopy technique that allows the study of ultrafast phenomena inside systems in condensed phase.[1] The term electronic refers to the fact that the optical frequencies in the visible spectral range are used to excite electronic energy states of the system; however, such a technique is also used in the IR optical range (excitation of vibrational states) and in this case the method is called two-dimensional infrared spectroscopy (2DIR).[2] This technique records the signal which is emitted from a system after an interaction with a sequence of 3 laser pulses. Such pulses usually have a time duration of few hundred femtosecond (10−15 s) and this high time resolution allows capturing of dynamics inside the system that evolves with the same time scale. The main result of this technique is a two-dimensional absorption spectrum that shows the correlation between excitation and detection frequencies. The first 2DES spectra were recorded in 1998 [3]

Basic concepts about 2DES

Pulse sequence

The pulse sequence in this experiment is the same as 2DIR in which the delay between the first and second pulse is called the coherence time and is usually labeled as [math]\displaystyle{ t_1 }[/math]. The delay between the second and the third pulse is called the population time and it is labeled as [math]\displaystyle{ t_2 }[/math]. The time after the third pulse corresponds to the detection time [math]\displaystyle{ t_3 }[/math] which is usually Fourier transformed by a spectrometer.[clarification needed] The interaction with the pulses creates a third-order nonlinear response function [math]\displaystyle{ S(t_1,t_2,t_3) }[/math] of the system from which it is possible to extract two-dimensional spectra as a function of excitation and detection frequencies.[4]

2D Signal

A possible way to recover an analytical expression of the response function is to consider the system as an ensemble and deal with the light-matter interaction process by using the density matrix approach.[4] Such a result shows that the response function is proportional to the product of the three pulses' electric fields. Considering [math]\displaystyle{ \vec{k_1},\vec{k_2},\vec{k_3} }[/math] the wave vectors of the three pulses, the nonlinear signal will emit in several directions [math]\displaystyle{ \vec{k_s} }[/math] which are derived from a linear combination of the three wave vectors: [math]\displaystyle{ \vec{k_s}=\pm \vec{k_1}\pm \vec{k_2}\pm \vec{k_3} }[/math]. For this technique, two different signals which propagate in different directions are usually taken into account. When [math]\displaystyle{ \vec{k_s}=-\vec{k_1}+\vec{k_2}+\vec{k_3} }[/math] the signal is called rephasing and when [math]\displaystyle{ \vec{k_s}=\vec{k_1}-\vec{k_2}+\vec{k_3} }[/math] the signal is called non-rephasing. An interpretation of these signals is possible by considering the system to be composed of many electric dipoles. When the first pulse interacts with the system, the dipoles start to oscillate in phase. The signal generated from each dipole rapidly dephases due to the different interaction that each dipole experienced with the environment. The interaction with the third pulse, in the case of rephasing, generates a signal which has an opposite temporal evolution with respect to the previous one. The dephasing of the last signal during [math]\displaystyle{ t_3 }[/math] compensates the one during [math]\displaystyle{ t_1 }[/math]. When [math]\displaystyle{ t_3=t_1 }[/math] the oscillations are in-phase again and the new signal generated is called photon echo. In the other case, there is no creation of a photon echo and the signal is called non-rephasing.

From these signals is possible to extract the pure absorptive and dispersive spectra which are usually shown in literature. The real part of the sum of these two signals represents the absorption of the system and the imaginary part contains the dispersion contribution.[5] In the absorptive 2D spectra, the sign of the peak implies different effects. If the transmitted signal is plotted, a positive peak can be associated to a bleaching signal with respect to the ground state or stimulated emission. If the sign is negative, that peak on the 2D spectra is associated with a photoinduced absorption.

Acquisition of the 2DES spectra

The first and the second pulses act as a pump and the third as a probe. The time-domain nonlinear response of the system interferes with another pulse called local oscillator (LO) which allows measurement of both amplitude and phase. Such a signal is usually acquired with a spectrometer which separates the contribution of each spectral components (detection frequencies [math]\displaystyle{ \nu_3 }[/math]). The acquisition proceeds by scanning the delay [math]\displaystyle{ t_1 }[/math] for a fixed delay [math]\displaystyle{ t_2 }[/math]. Once the scan ends, the detector has acquired a signal as a function of coherence time per each detection frequency [math]\displaystyle{ S(t_1,t_2,\nu_3) }[/math]. The application of the Fourier transform along the [math]\displaystyle{ t_1 }[/math] axis allows for recovery of the excitation spectra for every [math]\displaystyle{ \nu_3 }[/math]. The result of this procedure is a 2D map that shows the correlation between excitation ([math]\displaystyle{ \nu_1 }[/math]) and detection frequency ([math]\displaystyle{ \nu_3 }[/math]) at a fixed population time [math]\displaystyle{ S(\nu_1,t_2,\nu_3) }[/math]. The time evolution of the system can be measured by repeating the procedure described before for different values of [math]\displaystyle{ t_2 }[/math].

There are several methods to implement this technique, all of which are based on the different configurations of the pulses.[6] Two examples of possible implementations are the "boxcar geometry" and the "partially collinear geometry". The boxcar geometry is a configuration where all the pulses arrive at the system from different directions [math]\displaystyle{ \vec{k_1}\neq\vec{k_2}\neq\vec{k_3} }[/math] this property allows acquiring separately the rephasing and non-rephasing signal. The partially collinear geometry is another implementation of this technique where the first and the second pulse coming from the same direction [math]\displaystyle{ \vec{k_1}=\vec{k_2}\neq\vec{k_3} }[/math]. In this case, the rephasing and non-rephasing signal are emitted in the same direction and it is possible to directly recover the absorptive and dispersive spectra of the system.[7][8]

Example of 2D spectra for 3 energy levels system (scheme on the right).

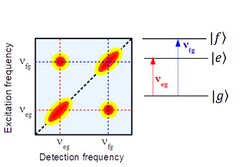
Information acquired from 2DES

2D spectra contain a lot of information about the system; in particular amplitude, position and lineshape of the peaks are related to different effects that happened inside of the system.

Position of the peaks

Diagonal Peaks

The peaks that stay along the diagonal line in the 2D spectra are called diagonal peaks. These peaks appear when the system emits a signal that oscillates at the same frequency of the excitation signal. These points reflect the information of the linear absorption spectrum.[5]

Cross Peaks

The peaks that stay out of the diagonal line are called cross peaks. These peaks appear when the system emits a signal that oscillates at a different frequency with respect to the signal used to excite. When a cross peak appears means that two electronic states of the system are coupled because when the pulses pump an electronic state, the system responds with emission from a different energy level. This coupling can be related to an energy transfer or charge transfer process between molecules.[4]

Lineshape of the peaks

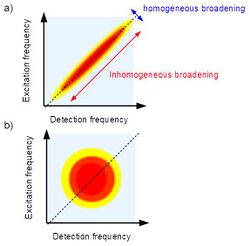
Lineshape Evolution: a)Example of the lineshape at population time close to zero b) Example of the line shape at large population time

Short population times

Thanks to the high spectral resolution, this technique acquires information based on the two dimensional shape of the peaks. When [math]\displaystyle{ t_2 }[/math] is close to zero the diagonal peaks show an elliptical lineshape as is shown in the figure on the right.[9] The width along the diagonal line represents the inhomogeneous broadening which contains information about interactions between the environment and the system. If the system is composed of a large amount of identical molecules, each of them interacts with the environment in a different way; this implies that the same electronic state of each molecule assumes different small variations. The value of the linewidth will be close to the one calculated in the linear absorption spectrum. On the other hand, the linewidth along the off-diagonal shows a smaller value with respect to the diagonal one. In this case the spectral broadening contains a contribution from a local interaction inside of the system; for this reason, the width reflects the homogeneous broadening.[5]

Long population times

For [math]\displaystyle{ t_2\gg 0 }[/math] fs, the shape of the peaks becomes circular and the width along diagonal and off-diagonal line are similar. This phenomenon takes place because all the molecules of the system experienced different local environments and the entire system lose memory of the initial condition. This effect is called Spectral Diffusion.[10]

Temporal lineshape evolution

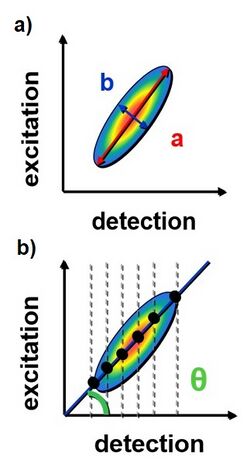
a) Example of a peak on 2D spectra where a and b are the linewidth along diagonal and off diagonal line. b) Example of an application of CLS method

The temporal evolution of the lineshape can be evaluated with several methods. One method evaluates the linewidth along diagonal and off-diagonal line separately.[11] From the two values of the widths it is possible to calculate the flattening as [math]\displaystyle{ f=\frac{a-b}{a} }[/math] where [math]\displaystyle{ a }[/math] is the linewidth along diagonal line and [math]\displaystyle{ b }[/math] is the linewidth along off-diagonal line. The flattening curve as a function of [math]\displaystyle{ t_2 }[/math] assumes a value close to 1 at [math]\displaystyle{ t_2=0 }[/math] fs ( [math]\displaystyle{ a\gg b }[/math]) and then decreases to zero at [math]\displaystyle{ t_2\gg 0 }[/math] fs ([math]\displaystyle{ a\simeq b }[/math]). Another method is called Central Line Slope (CLS).[12][13] In this case the positions of the maximum values in the 2D spectra per each detection frequency are considered. These points are then interpolated with a linear function where is possible to extract the slope [math]\displaystyle{ \theta }[/math] between this function and the detection axis (x axis). From a theoretical point of view, this value should be 45° when [math]\displaystyle{ t_2 }[/math] is close to zero because the peak is elongated along the diagonal line. When the peak assumes a circular lineshape, the value of the slope goes to zero. The same approach can also be used by considering the positions of the maximum values per each excitation frequency (y axis) and the slope will be 45° at [math]\displaystyle{ t_2=0 }[/math] fs and 90° when the shape becomes circular.[14]

See also

References

  1. ↑ Cho, Minhaeng (2009). Two-dimensional Optical Spectroscopy. CRC Press. 
  2. ↑ Hamm, Peter (2011). Concepts and methods of 2d infrared spectroscopy. Zanni, Martin T.. Cambridge: Cambridge University Press. ISBN 9781139040884. OCLC 710992325. 
  3. ↑ Hybl, J. D.; Albrecht, A. W.; Faeder, S. M. G.; Jonas, D. M. (1998). "Two-dimensional electronic spectroscopy". Chem. Phys. Lett. 297: 307–313. 
  4. ↑ 4.0 4.1 4.2 S. Mukamel (2000). "Multidimensional Femtosecond Correlation Spectroscopies of Electronic and Vibrational Excitations". Annual Review of Physical Chemistry 51: 691–729. doi:10.1146/annurev.physchem.51.1.691. PMID 11031297. Bibcode: 2000ARPC...51..691M. 
  5. ↑ 5.0 5.1 5.2 Cho, Minhaeng; Brixner, Tobias; Stiopkin, Igor; Vaswani, Harsha; Fleming, Graham R. (Feb 2006). "Two Dimensional Electronic Spectroscopy of Molecular Complexes". Journal of the Chinese Chemical Society 53 (1): 15–24. doi:10.1002/jccs.200600002. ISSN 0009-4536. 
  6. ↑ Fuller, Franklin D.; Ogilvie, Jennifer P. (2015-04-01). "Experimental Implementations of Two-Dimensional Fourier Transform Electronic Spectroscopy". Annual Review of Physical Chemistry 66 (1): 667–690. doi:10.1146/annurev-physchem-040513-103623. ISSN 0066-426X. PMID 25664841. 
  7. ↑ Brańczyk, Agata M.; Turner, Daniel B.; Scholes, Gregory D. (2014). "Crossing disciplines – A view on two-dimensional optical spectroscopy". Annalen der Physik 526 (1–2): 31–49. doi:10.1002/andp.201300153. ISSN 1521-3889. 
  8. ↑ Réhault, Julien; Maiuri, Margherita; Oriana, Aurelio; Cerullo, Giulio (2014-12-01). "Two-dimensional electronic spectroscopy with birefringent wedges". Review of Scientific Instruments 85 (12): 123107. doi:10.1063/1.4902938. ISSN 0034-6748. PMID 25554272. 
  9. ↑ Kwac, Kijeong; Cho, Minhaeng (2003). "Two-color pump-probe spectroscopies of two- and three-level systems: 2-Dimensional line shapes and solvation dynamics". J. Phys. Chem. A 107: 5903. 
  10. ↑ Roberts, Sean T.; Loparo, Joseph J.; Tokmakoff, Andrei (2006-08-22). "Characterization of spectral diffusion from two-dimensional line shapes". The Journal of Chemical Physics 125 (8): 084502. doi:10.1063/1.2232271. ISSN 0021-9606. PMID 16965024. 
  11. ↑ Kwac, Kijeong; Cho, Minhaeng (2003). "Two-color pump-probe spectroscopies of two- and three-level systems: 2-Dimensional line shapes and solvation dynamics". J. Phys. Chem. A 107: 5903. 
  12. ↑ Lazonder, Kees; Pshenichnikov, Maxim; Wiersma, Douwe (2006). "Easy interpretation of optical two-dimensional correlation spectra". Opt. Lett. 31 (22): 3354. doi:10.1364/OL.31.003354. 
  13. ↑ Roberts, Sean; Loparo, Joseph; Tokmakoff, Andrei (2006). "Characterization of spectral diffusion from two-dimensional line shapes". J. Phys. Chem. 125 (8): 084502. doi:10.1063/1.2232271. 
  14. ↑ Šanda, František; Perlík, Václav; Lincoln, Craig N.; Hauer, Jürgen (2015-11-05). "Center Line Slope Analysis in Two-Dimensional Electronic Spectroscopy". The Journal of Physical Chemistry A 119 (44): 10893–10909. doi:10.1021/acs.jpca.5b08909. ISSN 1089-5639. PMID 26463085. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Two-dimensional_electronic_spectroscopy&oldid=3283870"