Physics:Statistical ensemble (mathematical physics)

Short description: Idealization of a large number of atomic-sized systems

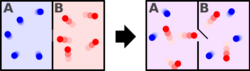
In physics, specifically statistical mechanics, an ensemble (also statistical ensemble) is an idealization consisting of a large number of virtual copies (sometimes infinitely many) of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a probability distribution for the state of the system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902.

A thermodynamic ensemble is a specific variety of statistical ensemble that, among other properties, is in statistical equilibrium (defined below), and is used to derive the properties of thermodynamic systems from the laws of classical or quantum mechanics.

Physical considerations

The ensemble formalises the notion that an experimenter repeating an experiment again and again under the same macroscopic conditions, but unable to control the microscopic details, may expect to observe a range of different outcomes.

The notional size of ensembles in thermodynamics, statistical mechanics and quantum statistical mechanics can be very large, including every possible microscopic state the system could be in, consistent with its observed macroscopic properties. For many important physical cases, it is possible to calculate averages directly over the whole of the thermodynamic ensemble, to obtain explicit formulas for many of the thermodynamic quantities of interest, often in terms of the appropriate partition function.

The concept of an equilibrium or stationary ensemble is crucial to many applications of statistical ensembles. Although a mechanical system certainly evolves over time, the ensemble does not necessarily have to evolve. In fact, the ensemble will not evolve if it contains all past and future phases of the system. Such a statistical ensemble, one that does not change over time, is called stationary and can be said to be in statistical equilibrium.

Terminology

• The word "ensemble" is also used for a smaller set of possibilities sampled from the full set of possible states. For example, a collection of walkers in a Markov chain Monte Carlo iteration is called an ensemble in some of the literature.
• The term "ensemble" is often used in physics and the physics-influenced literature. In probability theory, the term probability space is more prevalent.

Principal ensembles of statistical thermodynamics

Visual representation of five statistical ensembles (from left to right): microcanonical ensemble, canonical ensemble, grand canonical ensemble, isobaric-isothermal ensemble, isoenthalpic-isobaric ensemble

The study of thermodynamics is concerned with systems that appear to human perception to be "static" (despite the motion of their internal parts), and which can be described simply by a set of macroscopically observable variables. These systems can be described by statistical ensembles that depend on a few observable parameters, and which are in statistical equilibrium. Gibbs noted that different macroscopic constraints lead to different types of ensembles, with particular statistical characteristics. Three important thermodynamic ensembles were defined by Gibbs:

• Microcanonical ensemble or NVE ensemble—a statistical ensemble where the total energy of the system and the number of particles in the system are each fixed to particular values; each of the members of the ensemble are required to have the same total energy and particle number. The system must remain totally isolated (unable to exchange energy or particles with its environment) in order to stay in statistical equilibrium.
• Canonical ensemble or NVT ensemble—a statistical ensemble where the energy is not known exactly but the number of particles is fixed. In place of the energy, the temperature is specified. The canonical ensemble is appropriate for describing a closed system which is in, or has been in, weak thermal contact with a heat bath. In order to be in statistical equilibrium, the system must remain totally closed (unable to exchange particles with its environment) and may come into weak thermal contact with other systems that are described by ensembles with the same temperature.
• Grand canonical ensemble or μVT ensemble—a statistical ensemble where neither the energy nor particle number are fixed. In their place, the temperature and chemical potential are specified. The grand canonical ensemble is appropriate for describing an open system: one which is in, or has been in, weak contact with a reservoir (thermal contact, chemical contact, radiative contact, electrical contact, etc.). The ensemble remains in statistical equilibrium if the system comes into weak contact with other systems that are described by ensembles with the same temperature and chemical potential.

The calculations that can be made using each of these ensembles are explored further in their respective articles. Other thermodynamic ensembles can be also defined, corresponding to different physical requirements, for which analogous formulae can often similarly be derived. For example in the reaction ensemble, particle number fluctuations are only allowed to occur according to the stoichiometry of the chemical reactions which are present in the system.

Representations of statistical ensembles in statistical mechanics

The precise mathematical expression for a statistical ensemble has a distinct form depending on the type of mechanics under consideration (quantum or classical). In the classical case, the ensemble is a probability distribution over the microstates. In quantum mechanics, this notion, due to von Neumann, is a way of assigning a probability distribution over the results of each complete set of commuting observables. In classical mechanics, the ensemble is instead written as a probability distribution in phase space; the microstates are the result of partitioning phase space into equal-sized units, although the size of these units can be chosen somewhat arbitrarily.

Requirements for representations

Putting aside for the moment the question of how statistical ensembles are generated operationally, we should be able to perform the following two operations on ensembles A, B of the same system:

• Test whether A, B are statistically equivalent.
• If p is a real number such that 0 < p < 1, then produce a new ensemble by probabilistic sampling from A with probability p and from B with probability 1 – p.

Under certain conditions, therefore, equivalence classes of statistical ensembles have the structure of a convex set.

Quantum mechanical

A statistical ensemble in quantum mechanics (also known as a mixed state) is most often represented by a density matrix, denoted by [math]\displaystyle{ \hat{\rho} }[/math]. The density matrix provides a fully general tool that can incorporate both quantum uncertainties (present even if the state of the system were completely known) and classical uncertainties (due to a lack of knowledge) in a unified manner. Any physical observable X in quantum mechanics can be written as an operator, X̂. The expectation value of this operator on the statistical ensemble [math]\displaystyle{ \rho }[/math] is given by the following trace:

[math]\displaystyle{ \langle X \rangle = \operatorname{Tr}(\hat X \rho). }[/math]

This can be used to evaluate averages (operator X̂), variances (using operator X̂ ²), covariances (using operator X̂Ŷ), etc. The density matrix must always have a trace of 1: [math]\displaystyle{ \operatorname{Tr}{\hat{\rho}}=1 }[/math] (this essentially is the condition that the probabilities must add up to one).

In general, the ensemble evolves over time according to the von Neumann equation.

Equilibrium ensembles (those that do not evolve over time, [math]\displaystyle{ d\hat{\rho}/dt=0 }[/math]) can be written solely as a function of conserved variables. For example, the microcanonical ensemble and canonical ensemble are strictly functions of the total energy, which is measured by the total energy operator Ĥ (Hamiltonian). The grand canonical ensemble is additionally a function of the particle number, measured by the total particle number operator N̂. Such equilibrium ensembles are a diagonal matrix in the orthogonal basis of states that simultaneously diagonalize each conserved variable. In bra–ket notation, the density matrix is

[math]\displaystyle{ \hat \rho = \sum_i P_i |\psi_i\rangle \langle \psi_i | }[/math]

where the |ψ_i⟩, indexed by i, are the elements of a complete and orthogonal basis. (Note that in other bases, the density matrix is not necessarily diagonal.)

Classical mechanical

Evolution of an ensemble of classical systems in phase space (top). Each system consists of one massive particle in a one-dimensional potential well (red curve, lower figure). The initially compact ensemble becomes swirled up over time.

In classical mechanics, an ensemble is represented by a probability density function defined over the system's phase space. While an individual system evolves according to Hamilton's equations, the density function (the ensemble) evolves over time according to Liouville's equation.

In a mechanical system with a defined number of parts, the phase space has n generalized coordinates called q₁, ... q_n, and n associated canonical momenta called p₁, ... p_n. The ensemble is then represented by a joint probability density function ρ(p₁, ... p_n, q₁, ... q_n).

If the number of parts in the system is allowed to vary among the systems in the ensemble (as in a grand ensemble where the number of particles is a random quantity), then it is a probability distribution over an extended phase space that includes further variables such as particle numbers N₁ (first kind of particle), N₂ (second kind of particle), and so on up to N_s (the last kind of particle; s is how many different kinds of particles there are). The ensemble is then represented by a joint probability density function ρ(N₁, ... N_s, p₁, ... p_n, q₁, ... q_n). The number of coordinates n varies with the numbers of particles.

Any mechanical quantity X can be written as a function of the system's phase. The expectation value of any such quantity is given by an integral over the entire phase space of this quantity weighted by ρ:

[math]\displaystyle{ \langle X \rangle = \sum_{N_1 = 0}^{\infty} \ldots \sum_{N_s = 0}^{\infty} \int \ldots \int \rho X \, dp_1 \ldots dq_n. }[/math]

The condition of probability normalization applies, requiring

[math]\displaystyle{ \sum_{N_1 = 0}^{\infty} \ldots \sum_{N_s = 0}^{\infty} \int \ldots \int \rho \, dp_1 \ldots dq_n = 1. }[/math]

Phase space is a continuous space containing an infinite number of distinct physical states within any small region. In order to connect the probability density in phase space to a probability distribution over microstates, it is necessary to somehow partition the phase space into blocks that are distributed representing the different states of the system in a fair way. It turns out that the correct way to do this simply results in equal-sized blocks of canonical phase space, and so a microstate in classical mechanics is an extended region in the phase space of canonical coordinates that has a particular volume. In particular, the probability density function in phase space, ρ, is related to the probability distribution over microstates, P by a factor

[math]\displaystyle{ \rho = \frac{1}{h^n C} P, }[/math]

where

• h is an arbitrary but predetermined constant with the units of energy×time, setting the extent of the microstate and providing correct dimensions to ρ.
• C is an overcounting correction factor (see below), generally dependent on the number of particles and similar concerns.

Since h can be chosen arbitrarily, the notional size of a microstate is also arbitrary. Still, the value of h influences the offsets of quantities such as entropy and chemical potential, and so it is important to be consistent with the value of h when comparing different systems.

Correcting overcounting in phase space

Typically, the phase space contains duplicates of the same physical state in multiple distinct locations. This is a consequence of the way that a physical state is encoded into mathematical coordinates; the simplest choice of coordinate system often allows a state to be encoded in multiple ways. An example of this is a gas of identical particles whose state is written in terms of the particles' individual positions and momenta: when two particles are exchanged, the resulting point in phase space is different, and yet it corresponds to an identical physical state of the system. It is important in statistical mechanics (a theory about physical states) to recognize that the phase space is just a mathematical construction, and to not naively overcount actual physical states when integrating over phase space. Overcounting can cause serious problems:

• Dependence of derived quantities (such as entropy and chemical potential) on the choice of coordinate system, since one coordinate system might show more or less overcounting than another.
• Erroneous conclusions that are inconsistent with physical experience, as in the mixing paradox.
• Foundational issues in defining the chemical potential and the grand canonical ensemble.

It is in general difficult to find a coordinate system that uniquely encodes each physical state. As a result, it is usually necessary to use a coordinate system with multiple copies of each state, and then to recognize and remove the overcounting.

A crude way to remove the overcounting would be to manually define a subregion of phase space that includes each physical state only once and then exclude all other parts of phase space. In a gas, for example, one could include only those phases where the particles' x coordinates are sorted in ascending order. While this would solve the problem, the resulting integral over phase space would be tedious to perform due to its unusual boundary shape. (In this case, the factor C introduced above would be set to C = 1, and the integral would be restricted to the selected subregion of phase space.)

A simpler way to correct the overcounting is to integrate over all of phase space but to reduce the weight of each phase in order to exactly compensate the overcounting. This is accomplished by the factor C introduced above, which is a whole number that represents how many ways a physical state can be represented in phase space. Its value does not vary with the continuous canonical coordinates, so overcounting can be corrected simply by integrating over the full range of canonical coordinates, then dividing the result by the overcounting factor. However, C does vary strongly with discrete variables such as numbers of particles, and so it must be applied before summing over particle numbers.

As mentioned above, the classic example of this overcounting is for a fluid system containing various kinds of particles, where any two particles of the same kind are indistinguishable and exchangeable. When the state is written in terms of the particles' individual positions and momenta, then the overcounting related to the exchange of identical particles is corrected by using

[math]\displaystyle{ C = N_1! N_2! \ldots N_s!. }[/math]

This is known as "correct Boltzmann counting".

Ensembles in statistics

The formulation of statistical ensembles used in physics has now been widely adopted in other fields, in part because it has been recognized that the canonical ensemble or Gibbs measure serves to maximize the entropy of a system, subject to a set of constraints: this is the principle of maximum entropy. This principle has now been widely applied to problems in linguistics, robotics, and the like.

In addition, statistical ensembles in physics are often built on a principle of locality: that all interactions are only between neighboring atoms or nearby molecules. Thus, for example, lattice models, such as the Ising model, model ferromagnetic materials by means of nearest-neighbor interactions between spins. The statistical formulation of the principle of locality is now seen to be a form of the Markov property in the broad sense; nearest neighbors are now Markov blankets. Thus, the general notion of a statistical ensemble with nearest-neighbor interactions leads to Markov random fields, which again find broad applicability; for example in Hopfield networks.

Operational interpretation

In the discussion given so far, while rigorous, we have taken for granted that the notion of an ensemble is valid a priori, as is commonly done in physical context. What has not been shown is that the ensemble itself (not the consequent results) is a precisely defined object mathematically. For instance,

• It is not clear where this very large set of systems exists (for example, is it a gas of particles inside a container?)
• It is not clear how to physically generate an ensemble.

In this section, we attempt to partially answer this question.

Suppose we have a preparation procedure for a system in a physics lab: For example, the procedure might involve a physical apparatus and some protocols for manipulating the apparatus. As a result of this preparation procedure, some system is produced and maintained in isolation for some small period of time. By repeating this laboratory preparation procedure we obtain a sequence of systems X₁, X₂, ....,X_k, which in our mathematical idealization, we assume is an infinite sequence of systems. The systems are similar in that they were all produced in the same way. This infinite sequence is an ensemble.

In a laboratory setting, each one of these prepped systems might be used as input for one subsequent testing procedure. Again, the testing procedure involves a physical apparatus and some protocols; as a result of the testing procedure we obtain a yes or no answer. Given a testing procedure E applied to each prepared system, we obtain a sequence of values Meas (E, X₁), Meas (E, X₂), ...., Meas (E, X_k). Each one of these values is a 0 (or no) or a 1 (yes).

Assume the following time average exists:

[math]\displaystyle{ \sigma(E) = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{k=1}^N \operatorname{Meas}(E, X_k) }[/math]

For quantum mechanical systems, an important assumption made in the quantum logic approach to quantum mechanics is the identification of yes-no questions to the lattice of closed subspaces of a Hilbert space. With some additional technical assumptions one can then infer that states are given by density operators S so that:

[math]\displaystyle{ \sigma(E) = \operatorname{Tr}(E S). }[/math]

We see this reflects the definition of quantum states in general: A quantum state is a mapping from the observables to their expectation values.

See also

• Density matrix
• Ensemble (fluid mechanics)
• Phase space
• Liouville's theorem (Hamiltonian)
• Ensemble average (statistical mechanics)
• Replication (statistics)

External links

• Monte Carlo applet applied in statistical physics problems.