Physics:Ultraviolet catastrophe
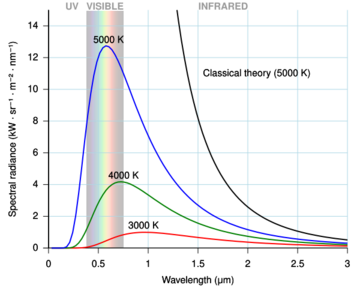
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was the prediction of late 19th century to early 20th century classical physics that an ideal black body at thermal equilibrium would emit an unbounded quantity of energy as wavelength decreased into the ultraviolet range.[1]:6-7 The term "ultraviolet catastrophe" was first used in 1911 by Paul Ehrenfest,[2] but the concept originated with the 1900 statistical derivation of the Rayleigh–Jeans law.
The phrase refers to the fact that the empirically derived Rayleigh–Jeans law, which accurately predicted experimental results at large wavelengths, failed to do so for short wavelengths. (See the image for further elaboration.) As the theory diverged from empirical observations when these frequencies reached the ultraviolet region of the electromagnetic spectrum, there was a problem.[3] This problem was later found to be due to a property of quanta as proposed by Max Planck: There could be no fraction of a discrete energy package already carrying minimal energy.
Since the first use of this term, it has also been used for other predictions of a similar nature, as in quantum electrodynamics and such cases as ultraviolet divergence.
Problem
The Rayleigh-Jeans law is an approximation to the spectral radiance of electromagnetic radiation as a function of wavelength from a black body at a given temperature through classical arguments. For wavelength [math]\displaystyle{ \lambda }[/math], it is:
- [math]\displaystyle{ B_{\lambda} (T) = \frac{2 ck_{\mathrm{B}} T}{\lambda^4}, }[/math]
where [math]\displaystyle{ B_{\lambda} }[/math] is the spectral radiance, the power emitted per unit emitting area, per steradian, per unit wavelength; [math]\displaystyle{ c }[/math] is the speed of light; [math]\displaystyle{ k_{\mathrm{B}} }[/math] is the Boltzmann constant; and [math]\displaystyle{ T }[/math] is the temperature in kelvins. For frequency [math]\displaystyle{ \nu }[/math], the expression is instead
- [math]\displaystyle{ B_{\nu}(T) = \frac{2 \nu^2 k_{\mathrm{B}} T}{c^2}. }[/math]
This formula is obtained from the equipartition theorem of classical statistical mechanics which states that all harmonic oscillator modes (degrees of freedom) of a system at equilibrium have an average energy of [math]\displaystyle{ k_{\rm B}T }[/math].
The "ultraviolet catastrophe" is the expression of the fact that the formula misbehaves at higher frequencies, i.e. [math]\displaystyle{ B_{\nu}(T) \to \infty }[/math] as [math]\displaystyle{ \nu \to \infty }[/math].
An example, from Mason's A History of the Sciences,[4] illustrates multi-mode vibration via a piece of string. As a natural vibrator, the string will oscillate with specific modes (the standing waves of a string in harmonic resonance), dependent on the length of the string. In classical physics, a radiator of energy will act as a natural vibrator. Additionally, since each mode will have the same energy, most of the energy in a natural vibrator will be in the smaller wavelengths and higher frequencies, where most of the modes are.
According to classical electromagnetism, the number of electromagnetic modes in a 3-dimensional cavity, per unit frequency, is proportional to the square of the frequency. This implies that the radiated power per unit frequency should be proportional to frequency squared. Thus, both the power at a given frequency and the total radiated power is unlimited as higher and higher frequencies are considered: this is unphysical as the total radiated power of a cavity is not observed to be infinite, a point that was made independently by Einstein and by Lord Rayleigh and Sir James Jeans in 1905.
Solution
In 1900, Max Planck derived the correct form for the intensity spectral distribution function by making some strange (for the time) assumptions. In particular, Planck assumed that electromagnetic radiation can be emitted or absorbed only in discrete packets, called quanta, of energy: [math]\displaystyle{ E_\text{quanta}=h\nu=h\frac{c}{\lambda}, }[/math] where:
- h is Planck's constant,
- ν is the frequency of light,
- c is the speed of light,
- λ is the wavelength of light.
Planck's assumptions led to the correct form of the spectral distribution functions: [math]\displaystyle{ B_\lambda(\lambda, T) =\frac{2 hc^2}{\lambda^5} \frac{1}{ \exp\left(\frac{h c}{\lambda k_\mathrm{B}T}\right) - 1} }[/math] where:
- T is the absolute temperature of the body,
- kB is the Boltzmann constant,
- exp denotes the exponential function.
Albert Einstein (in 1905) solved the problem by postulating that Planck's quanta were real physical particles – what we now call photons, not just a mathematical fiction. They modified statistical mechanics in the style of Boltzmann to an ensemble of photons. Einstein's photon had an energy proportional to its frequency and also explained an unpublished law of Stokes and the photoelectric effect.[5] This published postulate was specifically cited by the Nobel Prize in Physics committee in their decision to award the prize for 1921 to Einstein.[6]
See also
- Wien approximation
- Vacuum catastrophe
- Planckian locus
References
- ↑ Vázquez, M.; Hanslmeier, Arnold (2005). Ultraviolet Radiation in the Solar System. Springer. ISBN 978-1-4020-3726-9. https://books.google.com/books?id=2ykUzupXUKgC.
- ↑ Ehrenfest 1911
- ↑ McQuarrie, Donald A.; Simon, John D. (1997). Physical chemistry: a molecular approach (rev. ed.). Sausalito, Calif.: Univ. Science Books. ISBN 978-0-935702-99-6.
- ↑ Mason, Stephen F. (1962). A History of the Sciences. Collier Books. p. 550. https://archive.org/details/historyofscience00maso.
- ↑ Stone, A. Douglas (2013). Einstein and the Quantum. Princeton University Press. ISBN 9780691139685. https://archive.org/details/einsteinquantumq0000ston.
- ↑ "The Nobel Prize in Physics: 1921". Nobel Media AB. 2017. https://www.nobelprize.org/nobel_prizes/physics/laureates/1921/. "For his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect."
Bibliography
Further reading
- Kroemer, Herbert; Kittel, Charles (1980). "Chapter 4". Thermal Physics (2 ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë; Franck (1977). Quantum Mechanics: Volume One. Hermann, Paris. pp. 624–626. ISBN 0-471-16433-X.
 |

