Steradian
| steradian | |
|---|---|
 A graphical representation of two different steradians.The sphere has radius r, and in this case the area A of the highlighted spherical cap is r2. The solid angle Ω equals [A/r2] sr which is 1 sr in this example. The entire sphere has a solid angle of 4π sr. | |
| General information | |
| Unit system | SI |
| Unit of | solid angle |
| Symbol | sr |
| Conversions | |
| 1 sr in ... | ... is equal to ... |
| SI base units | 1 m2/m2 |
| square degrees | 32400/π2 deg2 ≈ 3282.8 deg2 |
The steradian (symbol: sr) or square radian[1][2] is the unit of solid angle in the International System of Units (SI). It is used in three dimensional geometry, and is analogous to the radian, which quantifies planar angles. Whereas an angle in radians, projected onto a circle, gives a length of a circular arc on the circumference, a solid angle in steradians, projected onto a sphere, gives the area of a spherical cap on the surface. The name is derived from the Greek στερεός stereos 'solid' + radian.
The steradian is a dimensionless unit, the quotient of the area subtended and the square of its distance from the centre. Both the numerator and denominator of this ratio have dimension length squared (i.e. L2/L2 = 1, dimensionless). It is useful, however, to distinguish between dimensionless quantities of a different kind, such as the radian (a ratio of quantities of dimension length), so the symbol "sr" is used to indicate a solid angle. For example, radiant intensity can be measured in watts per steradian (W⋅sr−1). The steradian was formerly an SI supplementary unit, but this category was abolished in 1995 and the steradian is now considered an SI derived unit.
Definition
A steradian can be defined as the solid angle subtended at the centre of a unit sphere by a unit area on its surface. For a general sphere of radius r, any portion of its surface with area A = r2 subtends one steradian at its centre.[3]
The solid angle is related to the area it cuts out of a sphere: [math]\displaystyle{ \Omega = \frac{A}{r^2}\ \text{sr} \, = \frac{2\pi h}{r}\ \text{sr}, }[/math] where
- Ω is the solid angle
- A is the surface area of the spherical cap, [math]\displaystyle{ 2\pi rh }[/math],
- r is the radius of the sphere,
- h is the height of the cap, and
- sr is the unit, steradian.
Because the surface area A of a sphere is 4πr2, the definition implies that a sphere subtends 4π steradians (≈ 12.56637 sr) at its centre, or that a steradian subtends 1/4π ≈ 0.07958 of a sphere. By the same argument, the maximum solid angle that can be subtended at any point is 4π sr.
Other properties
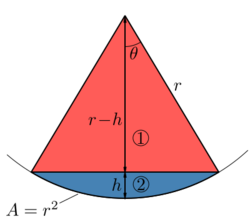
If A = r2, it corresponds to the area of a spherical cap (A = 2πrh, where h is the "height" of the cap) and the relationship [math]\displaystyle{ \tfrac{h}{r} = \tfrac{1}{2\pi} }[/math] holds. Therefore, in this case, one steradian corresponds to the plane (i.e. radian) angle of the cross-section of a simple cone subtending the plane angle 2θ, with θ given by:
[math]\displaystyle{ \begin{align} \theta & = \arccos \left( \frac{r-h}{r} \right)\\ & = \arccos \left( 1 - \frac{h}{r} \right)\\ & = \arccos \left( 1 - \frac{1}{2\pi} \right) \approx 0.572 \text{ rad, or } 32.77^\circ. \end{align} }[/math]
This angle corresponds to the plane aperture angle of 2θ ≈ 1.144 rad or 65.54°.
A steradian is also equal to the spherical area of a polygon having an angle excess of 1 radian, to [math]\displaystyle{ \tfrac{1}{4\pi} }[/math] of a complete sphere, or to [math]\displaystyle{ \left(\tfrac{180^\circ}{\pi}\right)^2 \approx }[/math] 3282.80635 square degrees.
The solid angle of a cone whose cross-section subtends the angle 2θ is: [math]\displaystyle{ \Omega = 2\pi\left(1 - \cos\theta\right) \text{ sr} = 4\pi\sin^2 \left(\frac{\theta}{2}\right) \text{ sr}. }[/math]
SI multiples
Millisteradians (msr) and microsteradians (μsr) are occasionally used to describe light and particle beams.[4][5] Other multiples are rarely used.
See also
- n-sphere
- Spat (angular unit)
- IAU designated constellations by area
References
- ↑ Stutzman, Warren L; Thiele, Gary A (2012-05-22). Antenna Theory and Design. ISBN 978-0-470-57664-9. https://books.google.com/books?id=xhZRA1K57wIC&q=steradian%20%22square%20radian%22&pg=PA51.
- ↑ Woolard, Edgar (2012-12-02). Spherical Astronomy. ISBN 978-0-323-14912-9. https://books.google.com/books?id=zLKQXGFUMPkC&q=steradian%20%22square%20radian%22&pg=PA11.
- ↑ "Steradian", McGraw-Hill Dictionary of Scientific and Technical Terms, fifth edition, Sybil P. Parker, editor in chief. McGraw-Hill, 1997. ISBN:0-07-052433-5.
- ↑ Stephen M. Shafroth, James Christopher Austin, Accelerator-based Atomic Physics: Techniques and Applications, 1997, ISBN 1563964848, p. 333
- ↑ R. Bracewell, Govind Swarup, "The Stanford microwave spectroheliograph antenna, a microsteradian pencil beam interferometer" IRE Transactions on Antennas and Propagation 9:1:22-30 (1961)
External links
 |  |
