Physics:Versor

Versors i, j, k of the Cartesian axes x, y, z for a three-dimensional Euclidean space. Every vector a in that space is a linear combination of these versors.

In geometry and physics, the versor of an axis or of a vector is a unit vector indicating its direction.

The versor of a Cartesian axis is also known as a standard basis vector. The versor of a vector is also known as a normalized vector.

Versors of a Cartesian coordinate system

The versors of the axes of a Cartesian coordinate system are the unit vectors codirectional with the axes of that system. Every Euclidean vector a in a n-dimensional Euclidean space (Rⁿ) can be represented as a linear combination of the n versors of the corresponding Cartesian coordinate system. For instance, in a three-dimensional space (R³), there are three versors:

[math]\displaystyle{ \mathbf{i} = (1,0,0), }[/math]

[math]\displaystyle{ \mathbf{j} = (0,1,0), }[/math]

[math]\displaystyle{ \mathbf{k} = (0,0,1). }[/math]

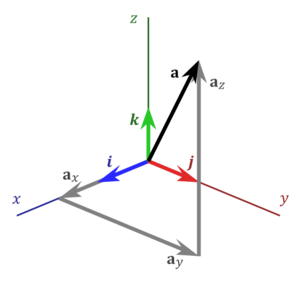
They indicate the direction of the Cartesian axes x, y, and z, respectively. In terms of these, any vector a can be represented as

[math]\displaystyle{ \mathbf{a} = \mathbf{a}_x + \mathbf{a}_y + \mathbf{a}_z = a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k}, }[/math]

where a_x, a_y, a_z are called the vector components (or vector projections) of a on the Cartesian axes x, y, and z (see figure), while a_x, a_y, a_z are the respective scalar components (or scalar projections).

In linear algebra, the set formed by these n versors is typically referred to as the standard basis of the corresponding Euclidean space, and each of them is commonly called a standard basis vector.

Notation

A hat above the symbol of a versor is sometimes used to emphasize its status as a unit vector (e.g., [math]\displaystyle{ \hat{\bold{\imath}} }[/math]).

In most contexts it can be assumed that i, j, and k, (or [math]\displaystyle{ \vec{\imath}, }[/math] [math]\displaystyle{ \vec{\jmath}, }[/math] and [math]\displaystyle{ \vec{k} }[/math]) are versors of a 3-D Cartesian coordinate system. The notations [math]\displaystyle{ (\hat{\bold{x}}, \hat{\bold{y}}, \hat{\bold{z}}) }[/math], [math]\displaystyle{ (\hat{\bold{x}}_1, \hat{\bold{x}}_2, \hat{\bold{x}}_3) }[/math], [math]\displaystyle{ (\hat{\bold{e}}_x, \hat{\bold{e}}_y, \hat{\bold{e}}_z) }[/math], or [math]\displaystyle{ (\hat{\bold{e}}_1, \hat{\bold{e}}_2, \hat{\bold{e}}_3) }[/math], with or without hat, are also used, particularly in contexts where i, j, k might lead to confusion with another quantity. This is recommended, for instance, when index symbols such as i, j, k are used to identify an element of a set of variables.

Versor of a non-zero vector

The versor (or normalized vector) [math]\displaystyle{ \hat{\mathbf{u}} }[/math] of a non-zero vector [math]\displaystyle{ \mathbf{u} }[/math] is the unit vector codirectional with [math]\displaystyle{ \mathbf{u} }[/math]:

[math]\displaystyle{ \hat{\mathbf{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|}. }[/math]

where [math]\displaystyle{ \|\mathbf{u}\| }[/math] is the norm (or length) of [math]\displaystyle{ \mathbf{u} }[/math]. Notice that a versor lost the units of the original vector. For instance, if we have the vector [math]\displaystyle{ \vec{u} = (0, 5, 0)\, \mathrm{m} }[/math], then [math]\displaystyle{ |\vec{u}| = \sqrt{0^2 + 5^2 + 0^2}\, \mathrm{m} = 5\, \mathrm{m} }[/math] and

[math]\displaystyle{ \hat{u} = \frac{\vec{u}}{|\vec{u}|} = \frac{(0, 5, 0)\, \mathrm{m}}{5\, \mathrm{m}} = (0, 1, 0) }[/math]

You can notice that [math]\displaystyle{ \hat{u} }[/math] is a dimensionless quantity.