Physics:Wiswesser rule
The Wiswesser rule gives a simple method to determine the energetic sequence of the atomic subshells [math]\displaystyle{ (n,\ell) }[/math], where n is the principal quantum number and ℓ is the azimuthal quantum number corresponding to s, p, d, f... of each atomic orbital. The energetic sequence of the subshells characterized by the quantum numbers [math]\displaystyle{ (n,\ell) }[/math] is the sequence that leads to a monotonically increasing row of function values for the Wiswesser function. The rule is named after William Wiswesser.
- [math]\displaystyle{ W(n,\ell) = n + \ell - \frac\ell{\ell + 1} }[/math]
For example: if [math]\displaystyle{ n = 2 }[/math] and [math]\displaystyle{ \ell = 1 }[/math], this corresponds to a 2p orbital.
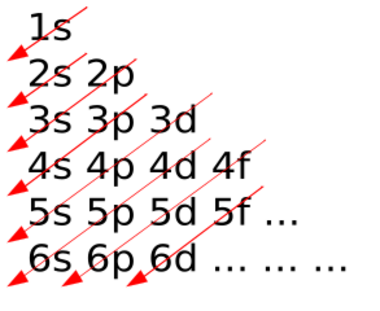
If the results of this function for each shell and subshell are ordered, the resulting sequence is: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p... This order of filling electron shells is the same as what the aufbau principle predicts.
To illustrate this, the corresponding values of each of these shells can be found in the table below:
| [math]\displaystyle{ n }[/math] | [math]\displaystyle{ \ell }[/math] | [math]\displaystyle{ W(n,\ell) }[/math] |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 0 | 2 |
| 2 | 1 | 2.5 |
| 3 | 0 | 3 |
| 3 | 1 | 3.5 |
| 3 | 2 | 4.33 |
| 4 | 0 | 4 |
| 4 | 1 | 4.5 |
| 4 | 2 | 5.33 |
| 4 | 3 | 6.25 |
| 5 | 0 | 5 |
| 5 | 1 | 5.5 |
| 5 | 2 | 6.33 |
| 5 | 3 | 7.25 |
| 5 | 4 | 8.2 |
| 6 | 0 | 6 |
| 6 | 1 | 6.5 |
| 6 | 2 | 7.33 |
| 6 | 3 | 8.25 |
| 6 | 4 | 9.2 |
| 6 | 5 | 10.16 |
| 7 | 0 | 7 |
| 7 | 1 | 7.5 |
| 7 | 2 | 8.33 |
| 7 | 3 | 9.25 |
| 7 | 4 | 10.2 |
| 7 | 5 | 11.16 |
| 8 | 0 | 8 |
| 8 | 1 | 8.5 |
| 8 | 2 | 9.33 |
| 8 | 3 | 10.25 |
| 8 | 4 | 11.2 |
| 8 | 5 | 12.16 |
See also
References