Physics:Magnetic quantum number

Short description: Number describing angular momentum along an axis

In atomic physics, a magnetic quantum number is a quantum number used to distinguish quantum states of an electron or other particle according to its angular momentum along a given axis in space. The orbital magnetic quantum number (m_l or m) distinguishes the orbitals available within a given subshell of an atom. It specifies the component of the orbital angular momentum that lies along a given axis, conventionally called the z-axis, so it describes the orientation of the orbital in space. The spin magnetic quantum number m_s specifies the z-axis component of the spin angular momentum for a particle having spin quantum number s. For an electron, s is ​¹⁄₂, and m_s is either +​¹⁄₂ or −​¹⁄₂, often called "spin-up" and "spin-down", or α and β. The term magnetic in the name refers to the magnetic dipole moment associated with each type of angular momentum, so states having different magnetic quantum numbers shift in energy in a magnetic field according to the Zeeman effect.

The four quantum numbers conventionally used to describe the quantum state of an electron in an atom are the principal quantum number n, the azimuthal (orbital) quantum number [math]\displaystyle{ \ell }[/math], and the magnetic quantum numbers m_l and m_s. Electrons in a given subshell of an atom (such as s, p, d, or f) are defined by values of [math]\displaystyle{ \ell }[/math] (0, 1, 2, or 3). The orbital magnetic quantum number takes integer values in the range from [math]\displaystyle{ -\ell }[/math] to [math]\displaystyle{ +\ell }[/math], including zero. Thus the s, p, d, and f subshells contain 1, 3, 5, and 7 orbitals each, with values of m_l within the ranges 0, ±1, ±2, ±3 respectively. Each of these orbitals can accommodate up to two electrons (with opposite spins), forming the basis of the periodic table.

Other magnetic quantum numbers are similarly defined, such as m_j for the z-axis component the total electronic angular momentum j, and m_I for the nuclear spin I. Magnetic quantum numbers are capitalized to indicate totals for a system of particles, such as M_L or m_L for the total z-axis orbital angular momentum of all the electrons in an atom.

Derivation

These orbitals have magnetic quantum numbers [math]\displaystyle{ m_l=-\ell, \ldots,\ell }[/math] from left to right in ascending order. The [math]\displaystyle{ e^{m_li\phi} }[/math] dependence of the azimuthal component can be seen as a color gradient repeating [math]\displaystyle{ m_l }[/math] times around the vertical axis.

There is a set of quantum numbers associated with the energy states of the atom. The four quantum numbers [math]\displaystyle{ n }[/math], [math]\displaystyle{ \ell }[/math], [math]\displaystyle{ m_l }[/math], and [math]\displaystyle{ m_s }[/math] specify the complete quantum state of a single electron in an atom called its wavefunction or orbital. The Schrödinger equation for the wavefunction of an atom with one electron is a separable partial differential equation. (This is not the case for the neutral helium atom or other atoms with mutually interacting electrons, which require more sophisticated methods for solution) This means that the wavefunction as expressed in spherical coordinates can be broken down into the product of three functions of the radius, colatitude (or polar) angle, and azimuth:

[math]\displaystyle{ \psi(r,\theta,\phi) = R(r)P(\theta)F(\phi) }[/math]

The differential equation for [math]\displaystyle{ F }[/math] can be solved in the form [math]\displaystyle{ F(\phi) = A e ^{\lambda\phi} }[/math]. Because values of the azimuth angle [math]\displaystyle{ \phi }[/math] differing by 2[math]\displaystyle{ \pi }[/math] radians (360 degrees) represent the same position in space, and the overall magnitude of [math]\displaystyle{ F }[/math] does not grow with arbitrarily large [math]\displaystyle{ \phi }[/math] as it would for a real exponent, the coefficient [math]\displaystyle{ \lambda }[/math] must be quantized to integer multiples of [math]\displaystyle{ i }[/math], producing an imaginary exponent: [math]\displaystyle{ \lambda = i m_l }[/math]. These integers are the magnetic quantum numbers. The same constant appears in the colatitude equation, where larger values of [math]\displaystyle{ {m_l}^2 }[/math] tend to decrease the magnitude of [math]\displaystyle{ P(\theta), }[/math] and values of [math]\displaystyle{ m_l }[/math] greater than the azimuthal quantum number [math]\displaystyle{ \ell }[/math] do not permit any solution for [math]\displaystyle{ P(\theta). }[/math]

Relationship between Quantum Numbers
Orbital	Values	Number of Values for [math]\displaystyle{ m_l }[/math]	Electrons per subshell
s	[math]\displaystyle{ \ell=0,\quad m_l=0 }[/math]	1	2
p	[math]\displaystyle{ \ell=1,\quad m_l=-1,0,+1 }[/math]	3	6
d	[math]\displaystyle{ \ell=2,\quad m_l=-2,-1,0,+1,+2 }[/math]	5	10
f	[math]\displaystyle{ \ell=3,\quad m_l = -3,-2,-1,0,+1,+2,+3 }[/math]	7	14
g	[math]\displaystyle{ \ell=4,\quad m_l = -4,-3,-2,-1,0,+1,+2,+3,+4 }[/math]	9	18

As a component of angular momentum

Illustration of quantum mechanical orbital angular momentum. The cones and plane represent possible orientations of the angular momentum vector for [math]\displaystyle{ \ell = 2 }[/math] and [math]\displaystyle{ m_l = -2, -1, 0, 1, 2 }[/math]. Even for the extreme values of [math]\displaystyle{ m_l }[/math], the [math]\displaystyle{ z }[/math]-component of this vector is less than its total magnitude.

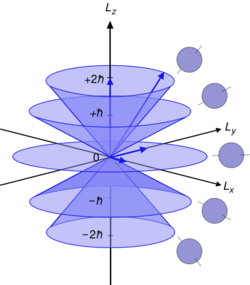
The axis used for the polar coordinates in this analysis is chosen arbitrarily. The quantum number [math]\displaystyle{ m_l }[/math] refers to the projection of the angular momentum in this arbitrarily-chosen direction, conventionally called the [math]\displaystyle{ z }[/math]-direction or quantization axis. [math]\displaystyle{ L_z }[/math], the magnitude of the angular momentum in the [math]\displaystyle{ z }[/math]-direction, is given by the formula:

[math]\displaystyle{ L_z = m_l \hbar }[/math].

This is a component of the atomic electron's total orbital angular momentum [math]\displaystyle{ \mathbf{L} }[/math], whose magnitude is related to the azimuthal quantum number of its subshell [math]\displaystyle{ \ell }[/math] by the equation:

[math]\displaystyle{ L = \hbar \sqrt{\ell (\ell + 1)} }[/math],

where [math]\displaystyle{ \hbar }[/math] is the reduced Planck constant. Note that this [math]\displaystyle{ L = 0 }[/math] for [math]\displaystyle{ \ell = 0 }[/math] and approximates [math]\displaystyle{ L = \left( \ell + \tfrac{1}{2} \right) \hbar }[/math] for high [math]\displaystyle{ \ell }[/math]. It is not possible to measure the angular momentum of the electron along all three axes simultaneously. These properties were first demonstrated in the Stern–Gerlach experiment, by Otto Stern and Walther Gerlach.

Effect in magnetic fields

The quantum number [math]\displaystyle{ m_l }[/math] refers, loosely, to the direction of the angular momentum vector. The magnetic quantum number [math]\displaystyle{ m_l }[/math] only affects the electron's energy if it is in a magnetic field because in the absence of one, all spherical harmonics corresponding to the different arbitrary values of [math]\displaystyle{ m_l }[/math] are equivalent. The magnetic quantum number determines the energy shift of an atomic orbital due to an external magnetic field (the Zeeman effect) — hence the name magnetic quantum number. However, the actual magnetic dipole moment of an electron in an atomic orbital arises not only from the electron angular momentum but also from the electron spin, expressed in the spin quantum number.

Since each electron has a magnetic moment in a magnetic field, it will be subject to a torque which tends to make the vector [math]\displaystyle{ \mathbf{L} }[/math] parallel to the field, a phenomenon known as Larmor precession.

See also

• Quantum number
  • Azimuthal quantum number
  • Principal quantum number
  • Spin quantum number
  • Total angular momentum quantum number
• Electron shell
• Basic quantum mechanics
• Bohr atom
• Schrödinger equation