Physics:Woods–Saxon potential
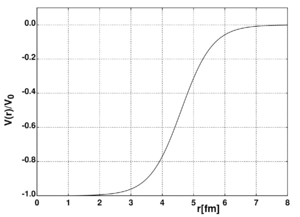
The Woods–Saxon potential is a mean field potential for the nucleons (protons and neutrons) inside the atomic nucleus, which is used to describe approximately the forces applied on each nucleon, in the nuclear shell model for the structure of the nucleus. The potential is named after Roger D. Woods and David S. Saxon.
The form of the potential, in terms of the distance r from the center of nucleus, is:
[math]\displaystyle{ V(r) = -\frac{V_0}{1+\exp({r-R\over a})} }[/math]
where V0 (having dimension of energy) represents the potential well depth, a is a length representing the "surface thickness" of the nucleus, and [math]\displaystyle{ R = r_0 A^{1/3} }[/math] is the nuclear radius where r0 = 1.25 fm and A is the mass number.
Typical values for the parameters are: V0 ≈ 50 MeV, a ≈ 0.5 fm.
For large atomic number A this potential is similar to a potential well. It has the following desired properties
- It is monotonically increasing with distance, i.e. attracting.
- For large A, it is approximately flat in the center.
- Nucleons near the surface of the nucleus (i.e. having r ≈ R within a distance of order a) experience a large force towards the center.
- It rapidly approaches zero as r goes to infinity (r − R >> a), reflecting the short-distance nature of the strong nuclear force.
The Schrödinger equation of this potential can be solved analytically, by transforming it into a hypergeometric differential equation. The radial part of the wavefunction solution is given by
[math]\displaystyle{ u(r)= \frac 1r y^\nu (1-y)^\mu {}_2F_1 (\mu+\nu, \mu+\nu+1; 2\nu+1; y) }[/math]
where [math]\displaystyle{ y = \dfrac{1}{1+\exp\left(\frac {r-R}{a}\right)} }[/math], [math]\displaystyle{ \mu = i\sqrt{\gamma^2-\nu^2} }[/math], [math]\displaystyle{ \dfrac{2mE}{\hbar^2}=-\nu^2 }[/math], [math]\displaystyle{ \nu \lt 0 }[/math] and [math]\displaystyle{ \dfrac{2mV_0}{\hbar^2}a^2=\gamma^2 }[/math].[1] Here [math]\displaystyle{ {}_2F_1(a,b;c;z) = \sum_{n=0}^\infty \frac{(a)_n (b)_n}{(c)_n} \frac{z^n}{n!} }[/math] is the hypergeometric function.
See also
- Finite potential well
- Quantum harmonic oscillator
- Particle in a box
- Yukawa potential
- Nuclear force
- Nuclear structure
- Shell model
References
- ↑ Flügge, Siegfried (1999). Practical Quantum Mechanics. Springer Berlin Heidelberg. pp. 162ff. ISBN 978-3-642-61995-3.
- Woods, R. D.; Saxon, D. S. (1954). "Diffuse Surface Optical Model for Nucleon-Nuclei Scattering". Physical Review 95 (2): 577–578. doi:10.1103/PhysRev.95.577. Bibcode: 1954PhRv...95..577W.
- Schwierz, N.; Wiedenhover, I.; Volya, A. (2007). "Parameterization of the Woods–Saxon Potential for Shell-Model Calculations". arXiv:0709.3525 [nucl-th].
- Flügge, Siegfried (1999). Practical Quantum Mechanics. Springer Berlin Heidelberg. pp. 162ff. ISBN 978-3-642-61995-3.
External links
 |

