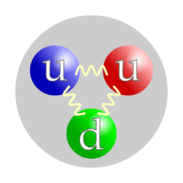
Physics:Nucleon

In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number (nucleon number).
Until the 1960s, nucleons were thought to be elementary particles, not made up of smaller parts. Now they are known to be composite particles, made of three quarks bound together by the strong interaction. The interaction between two or more nucleons is called internucleon interaction or nuclear force, which is also ultimately caused by the strong interaction. (Before the discovery of quarks, the term "strong interaction" referred to just internucleon interactions.)
Nucleons sit at the boundary where particle physics and nuclear physics overlap. Particle physics, particularly quantum chromodynamics, provides the fundamental equations that describe the properties of quarks and of the strong interaction. These equations describe quantitatively how quarks can bind together into protons and neutrons (and all the other hadrons). However, when multiple nucleons are assembled into an atomic nucleus (nuclide), these fundamental equations become too difficult to solve directly (see lattice QCD). Instead, nuclides are studied within nuclear physics, which studies nucleons and their interactions by approximations and models, such as the nuclear shell model. These models can successfully describe nuclide properties, as for example, whether or not a particular nuclide undergoes radioactive decay.
The proton and neutron are in a scheme of categories being at once fermions, hadrons and baryons. The proton carries a positive net charge, and the neutron carries a zero net charge; the proton's mass is only about 0.13% less than the neutron's. Thus, they can be viewed as two states of the same nucleon, and together form an isospin doublet (I = 1/2). In isospin space, neutrons can be transformed into protons and conversely by SU(2) symmetries. These nucleons are acted upon equally by the strong interaction, which is invariant under rotation in isospin space. According to Noether's theorem, isospin is conserved with respect to the strong interaction.[1]:129–130
Overview
Properties
Protons and neutrons are best known in their role as nucleons, i.e., as the components of atomic nuclei, but they also exist as free particles. Free neutrons are unstable, with a half-life of around 13 minutes, but they have important applications (see neutron radiation and neutron scattering). Protons not bound to other nucleons are the nuclei of hydrogen atoms when bound with an electron or – if not bound to anything – are ions or cosmic rays.
Both the proton and the neutron are composite particles, meaning that each is composed of smaller parts, namely three quarks each; although once thought to be so, neither is an elementary particle. A proton is composed of two up quarks and one down quark, while the neutron has one up quark and two down quarks. Quarks are held together by the strong force, or equivalently, by gluons, which mediate the strong force at the quark level.
An up quark has electric charge ++2/3 e, and a down quark has charge −+1/3 e, so the summed electric charges of proton and neutron are +e and 0, respectively.[lower-alpha 1] Thus, the neutron has a charge of 0 (zero), and therefore is electrically neutral; indeed, the term "neutron" comes from the fact that a neutron is electrically neutral.
The masses of the proton and neutron are similar: for the proton it is 1.6726×10−27 kg (938.27 MeV/c2), while for the neutron it is 1.6749×10−27 kg (939.57 MeV/c2); the neutron is roughly 0.13% heavier. The similarity in mass can be explained roughly by the slight difference in masses of up quarks and down quarks composing the nucleons. However, a detailed description remains an unsolved problem in particle physics.[1]:135–136
The spin of the nucleon is 1/2, which means that they are fermions and, like electrons, are subject to the Pauli exclusion principle: no more than one nucleon, e.g. in an atomic nucleus, may occupy the same quantum state.
The isospin and spin quantum numbers of the nucleon have two states each, resulting in four combinations in total. An alpha particle is composed of four nucleons occupying all four combinations, namely, it has two protons (having opposite spin) and two neutrons (also having opposite spin), and its net nuclear spin is zero. In larger nuclei constituent nucleons, by Pauli exclusion, are compelled to have relative motion, which may also contribute to nuclear spin via the orbital quantum number. They spread out into nuclear shells analogous to electron shells known from chemistry.
Both the proton and neutron have magnetic moments, though the nucleon magnetic moments are anomalous and were unexpected when they were discovered in the 1930s. The proton's magnetic moment, symbol μp, is 2.79 μN, whereas, if the proton were an elementary Dirac particle, it should have a magnetic moment of 1.0 μN. Here the unit for the magnetic moments is the nuclear magneton, symbol μN, an atomic-scale unit of measure. The neutron's magnetic moment is μn = −1.91 μN, whereas, since the neutron lacks an electric charge, it should have no magnetic moment. The value of the neutron's magnetic moment is negative because the direction of the moment is opposite to the neutron's spin. The nucleon magnetic moments arise from the quark substructure of the nucleons.[2][3] The proton magnetic moment is exploited for NMR / MRI scanning.
Stability
A neutron in free state is an unstable particle, with a half-life around ten minutes. It undergoes β− decay (a type of radioactive decay) by turning into a proton while emitting an electron and an electron antineutrino. This reaction can occur because the mass of the neutron is slightly greater than that of the proton. (See the Neutron article for more discussion of neutron decay.) A proton by itself is thought to be stable, or at least its lifetime is too long to measure. This is an important discussion in particle physics (see Proton decay).
Inside a nucleus, on the other hand, combined protons and neutrons (nucleons) can be stable or unstable depending on the nuclide, or nuclear species. Inside some nuclides, a neutron can turn into a proton (producing other particles) as described above; the reverse can happen inside other nuclides, where a proton turns into a neutron (producing other particles) through β+ decay or electron capture. And inside still other nuclides, both protons and neutrons are stable and do not change form.
Antinucleons
Both nucleons have corresponding antiparticles: the antiproton and the antineutron, which have the same mass and opposite charge as the proton and neutron respectively, and they interact in the same way. (This is generally believed to be exactly true, due to CPT symmetry. If there is a difference, it is too small to measure in all experiments to date.) In particular, antinucleons can bind into an "antinucleus". So far, scientists have created antideuterium[4][5] and antihelium-3[6] nuclei.
Tables of detailed properties
Nucleons
| Particle name |
Symbol | Quark content |
Mass[a] | I3 | JP | Q | Magnetic moment (μN) | Mean lifetime | Commonly decays to |
|---|---|---|---|---|---|---|---|---|---|
| proton[PDG 1] | p / p+ / N+ | Up quarkuDown quark | 1.00727646688 938.272013(23) MeV/c2 1.00727646677(10) Da
|
0.5 +1/2
|
0.5 1/2
+ |
1 +1 e
|
2.7 2.792847356(23)
|
+10 stable | unobserved |
| neutron[PDG 2] | n / n0 / N0 | udd | 1.00866491560 939.565346(23) MeV/c2 1.00866491597(43) Da
|
-0.5 −+1/2
|
0.5 1/2
+ |
0 0 e
|
-1.9 −1.91304273(45)
|
+2 885.7(8) s | Proton + e− + Electron antineutrino |
| antiproton | p / p− / N− | uud | 1.00727646688 938.272013(23) MeV/c2 1.00727646677(10) Da
|
-0.5 −+1/2
|
0.5 1/2
+ |
-1 −1 e
|
-2.7 −2.793(6)
|
+10 stable | unobserved |
| antineutron | n / n0 / N0 | udd | 1.00866491560 939.485(51) MeV/c2 1.00866491597(43) Da
|
0.5 ++1/2
|
0.5 1/2
+ |
0 0 e
|
? | +2 885.7(8) s | Antiproton + Positron + Electron neutrino |
^a The masses of the proton and neutron are known with far greater precision in daltons (Da) than in MeV/c2 due to the way in which these are defined. The conversion factor used is 1 Da = 931.494028(23) MeV/c2.
^b At least 1035 years. See proton decay.
^c For free neutrons; in most common nuclei, neutrons are stable.
The masses of their antiparticles are assumed to be identical, and no experiments have refuted this to date. Current experiments show any relative difference between the masses of the proton and antiproton must be less than 2×10−9[PDG 1] and the difference between the neutron and antineutron masses is on the order of (9±6)×10−5 MeV/c2.[PDG 2]
| Test | Formula | PDG result[PDG 1] |
|---|---|---|
| Mass | <2×10−9 | |
| Charge-to-mass ratio | 0.99999999991(9) | |
| Charge-to-mass-to-mass ratio | (−9±9)×10−11 | |
| Charge | <2×10−9 | |
| Electron charge | <1×10−21 | |
| Magnetic moment | (−0.1±2.1)×10−3 |
Nucleon resonances
Nucleon resonances are excited states of nucleon particles, often corresponding to one of the quarks having a flipped spin state, or with different orbital angular momentum when the particle decays. Only resonances with a 3- or 4-star rating at the Particle Data Group (PDG) are included in this table. Due to their extraordinarily short lifetimes, many properties of these particles are still under investigation.
The symbol format is given as N(m) LIJ, where m is the particle's approximate mass, L is the orbital angular momentum (in the spectroscopic notation) of the nucleon–meson pair, produced when it decays, and I and J are the particle's isospin and total angular momentum respectively. Since nucleons are defined as having 1/2 isospin, the first number will always be 1, and the second number will always be odd. When discussing nucleon resonances, sometimes the N is omitted and the order is reversed, in the form LIJ (m); for example, a proton can be denoted as "N(939) S11" or "S11 (939)".
The table below lists only the base resonance; each individual entry represents 4 baryons: 2 nucleon resonances particles and their 2 antiparticles. Each resonance exists in a form with a positive electric charge (Q), with a quark composition of uud like the proton, and a neutral form, with a quark composition of udd like the neutron, as well as the corresponding antiparticles with antiquark compositions of uud and udd respectively. Since they contain no strange, charm, bottom, or top quarks, these particles do not possess strangeness, etc.
The table only lists the resonances with an isospin = 1/2. For resonances with isospin = 3/2, see the article on Delta baryons.
| Symbol | JP | PDG mass average (MeV/c2) |
Full width (MeV/c2) |
Pole position (real part) |
Pole position (−2 × imaginary part) |
Common decays (Γi/Γ > 50%) |
|---|---|---|---|---|---|---|
| N(939) P11 [PDG 3]† |
0.5 1/2
+ |
939 | † | † | † | † |
| N(1440) P11 [PDG 4] (the Roper resonance) |
0.5 1/2
+ |
1440 (1420–1470) |
300 (200–450) |
1365 (1350–1380) |
190 (160–220) |
Nucleon + Pion |
| N(1520) D13 [PDG 5] |
1.5 3/2
− |
1520 (1515–1525) |
115 (100–125) |
1510 (1505–1515) |
110 (105–120) |
Nucleon + Pion |
| N(1535) S11 [PDG 6] |
0.5 1/2
− |
1535 (1525–1545) |
150 (125–175) |
1510 (1490–1530) |
170 (90–250) |
Nucleon + Pion or Nucleon + Eta |
| N(1650) S11 [PDG 7] |
0.5 1/2
− |
1650 (1645–1670) |
165 (145–185) |
1665 (1640–1670) |
165 (150–180) |
Nucleon + Pion |
| N(1675) D15 [PDG 8] |
2.5 5/2
− |
1675 (1670–1680) |
150 (135–165) |
1660 (1655–1665) |
135 (125–150) |
Nucleon + Pion + Pion or Delta + Pion |
| N(1680) F15 [PDG 9] |
2.5 5/2
+ |
1685 (1680–1690) |
130 (120–140) |
1675 (1665–1680) |
120 (110–135) |
Nucleon + Pion |
| N(1700) D13 [PDG 10] |
1.5 3/2
− |
1700 (1650–1750) |
100 (50–150) |
1680 (1630–1730) |
100 (50–150) |
Nucleon + Pion + Pion |
| N(1710) P11 [PDG 11] |
0.5 1/2
+ |
1710 (1680–1740) |
100 (50–250) |
1720 (1670–1770) |
230 (80–380) |
Nucleon + Pion + Pion |
| N(1720) P13 [PDG 12] |
1.5 3/2
+ |
1720 (1700–1750) |
200 (150–300) |
1675 (1660–1690) |
115–275 | Nucleon + Pion + Pion or Nucleon + Rho |
| N(2190) G17 [PDG 13] |
3.5 7/2
− |
2190 (2100–2200) |
500 (300–700) |
2075 (2050–2100) |
450 (400–520) |
Nucleon + Pion (10—20%) |
| N(2220) H19 [PDG 14] |
4.5 9/2
+ |
2250 (2200–2300) |
400 (350–500) |
2170 (2130–2200) |
480 (400–560) |
Nucleon + Pion (10—20%) |
| N(2250) G19 [PDG 15] |
4.5 9/2
− |
2250 (2200–2350) |
500 (230–800) |
2200 (2150–2250) |
450 (350–550) |
Nucleon + Pion (5—15%) |
† The P11(939) nucleon represents the excited state of a normal proton or neutron. Such a particle may be stable when in an atomic nucleus, e.g. in lithium-6.[7]
Quark model classification
In the quark model with SU(2) flavour, the two nucleons are part of the ground-state doublet. The proton has quark content of uud, and the neutron, udd. In SU(3) flavour, they are part of the ground-state octet (8) of spin-1/2 baryons, known as the Eightfold way. The other members of this octet are the hyperons strange isotriplet Σ+, Σ0, Σ−, the Λ and the strange isodoublet Ξ0, Ξ−. One can extend this multiplet in SU(4) flavour (with the inclusion of the charm quark) to the ground-state 20-plet, or to SU(6) flavour (with the inclusion of the top and bottom quarks) to the ground-state 56-plet.
The article on isospin provides an explicit expression for the nucleon wave functions in terms of the quark flavour eigenstates.
Models
Although it is known that the nucleon is made from three quarks, (As of 2006), it is not known how to solve the equations of motion for quantum chromodynamics. Thus, the study of the low-energy properties of the nucleon are performed by means of models. The only first-principles approach available is to attempt to solve the equations of QCD numerically, using lattice QCD. This requires complicated algorithms and very powerful supercomputers. However, several analytic models also exist:
Skyrmion models
The skyrmion models the nucleon as a topological soliton in a nonlinear SU(2) pion field. The topological stability of the skyrmion is interpreted as the conservation of baryon number, that is, the non-decay of the nucleon. The local topological winding number density is identified with the local baryon number density of the nucleon. With the pion isospin vector field oriented in the shape of a hedgehog space, the model is readily solvable, and is thus sometimes called the hedgehog model. The hedgehog model is able to predict low-energy parameters, such as the nucleon mass, radius and axial coupling constant, to approximately 30% of experimental values.
MIT bag model
The MIT bag model[8][9][10] confines quarks and gluons interacting through quantum chromodynamics to a region of space determined by balancing the pressure exerted by the quarks and gluons against a hypothetical pressure exerted by the vacuum on all colored quantum fields. The simplest approximation to the model confines three non-interacting quarks to a spherical cavity, with the boundary condition that the quark vector current vanish on the boundary. The non-interacting treatment of the quarks is justified by appealing to the idea of asymptotic freedom, whereas the hard-boundary condition is justified by quark confinement.
Mathematically, the model vaguely resembles that of a radar cavity, with solutions to the Dirac equation standing in for solutions to the Maxwell equations, and the vanishing vector current boundary condition standing for the conducting metal walls of the radar cavity. If the radius of the bag is set to the radius of the nucleon, the bag model predicts a nucleon mass that is within 30% of the actual mass.
Although the basic bag model does not provide a pion-mediated interaction, it describes excellently the nucleon–nucleon forces through the 6 quark bag s-channel mechanism using the P-matrix.[11][12]
Chiral bag model
The chiral bag model[13][14] merges the MIT bag model and the skyrmion model. In this model, a hole is punched out of the middle of the skyrmion and replaced with a bag model. The boundary condition is provided by the requirement of continuity of the axial vector current across the bag boundary.
Very curiously, the missing part of the topological winding number (the baryon number) of the hole punched into the skyrmion is exactly made up by the non-zero vacuum expectation value (or spectral asymmetry) of the quark fields inside the bag. (As of 2017), this remarkable trade-off between topology and the spectrum of an operator does not have any grounding or explanation in the mathematical theory of Hilbert spaces and their relationship to geometry.
Several other properties of the chiral bag are notable: It provides a better fit to the low-energy nucleon properties, to within 5–10%, and these are almost completely independent of the chiral-bag radius, as long as the radius is less than the nucleon radius. This independence of radius is referred to as the Cheshire Cat principle,[15] after the fading of Lewis Carroll's Cheshire Cat to just its smile. It is expected that a first-principles solution of the equations of QCD will demonstrate a similar duality of quark–meson descriptions.
See also
Footnotes
- ↑ The resultant coefficients are obtained by summation of the component charges: ΣQ = 2/3 + 2/3 + (−+1/3) = 3/3 = +1 for proton, and ΣQ = 2/3 + (−+1/3) + (−+1/3) = 0/3 = 0 for neutron.
References
- ↑ 1.0 1.1 Griffiths, David J. (2008). Introduction to Elementary Particles (2nd revised ed.). WILEY-VCH. ISBN 978-3-527-40601-2.
- ↑ Introduction to High Energy Physics. Reading, Massachusetts: Addison Wesley. 1982. pp. 201–202. ISBN 978-0-201-05757-7. https://archive.org/details/introductiontohi0000perk.
- ↑ Kincade, Kathy (2 February 2015). "Pinpointing the magnetic moments of nuclear matter". Phys.org. http://phys.org/news/2015-02-magnetic-moments-nuclear.html.
- ↑ Massam, T; Muller, Th.; Righini, B.; Schneegans, M.; Zichichi, A. (1965). "Experimental observation of antideuteron production". Il Nuovo Cimento 39 (1): 10–14. doi:10.1007/BF02814251. Bibcode: 1965NCimS..39...10M.
- ↑ Dorfan, D. E; Eades, J.; Lederman, L. M.; Lee, W.; Ting, C. C. (June 1965). "Observation of Antideuterons". Phys. Rev. Lett. 14 (24): 1003–1006. doi:10.1103/PhysRevLett.14.1003. Bibcode: 1965PhRvL..14.1003D.
- ↑ R. Arsenescu (2003). "Antihelium-3 production in lead-lead collisions at 158 A GeV/c". New Journal of Physics 5 (1): 1. doi:10.1088/1367-2630/5/1/301. Bibcode: 2003NJPh....5....1A.
- ↑ "Lithium-6. Compound summary". National Library of Medicine. https://pubchem.ncbi.nlm.nih.gov/compound/Lithium-6.
- ↑ Chodos et al. "New extended model of hadrons" , Phys. Rev. D 9, 3471 (1974).
- ↑ Chodos et al. "Baryon structure in the bag theory" , Phys. Rev. D 10, 2599 (1974).
- ↑ DeGrand et al. "Masses and other parameters of the light hadrons" , Phys. Rev. D 12, 2060 (1975).
- ↑ Jaffe, R. L.; Low, F. E. (1979). "Connection between quark-model eigenstates and low-energy scattering". Phys. Rev. D 19 (7): 2105. doi:10.1103/PhysRevD.19.2105. Bibcode: 1979PhRvD..19.2105J.
- ↑ Yu; Simonov, A. (1981). "The quark compound bag model and the Jaffe-Low P-matrix". Physics Letters B 107 (1–2): 1. doi:10.1016/0370-2693(81)91133-3. Bibcode: 1981PhLB..107....1S.
- ↑ "The little bag". Physics Letters B 82 (2): 177–180. March 1979. doi:10.1016/0370-2693(79)90729-9. Bibcode: 1979PhLB...82..177B.
- ↑ Vepstas, L.; Jackson, A. D.; Goldhaber, A. S. (1984). "Two-phase models of baryons and the chiral Casimir effect". Physics Letters B 140 (5–6): 280–284. doi:10.1016/0370-2693(84)90753-6. Bibcode: 1984PhLB..140..280V.
- ↑ Vepstas, L.; Jackson, A. D. (1990). "Justifying the chiral bag". Physics Reports 187 (3): 109–143. doi:10.1016/0370-1573(90)90056-8. Bibcode: 1990PhR...187..109V.
Particle listings
- ↑ 1.0 1.1 1.2 Particle listings – p .
- ↑ 2.0 2.1 Particle listings – n .
- ↑ Particle listings — Note on N and Delta Resonances .
- ↑ Particle listings — N(1440) .
- ↑ Particle listings — N(1520) .
- ↑ Particle listings — N(1535) .
- ↑ Particle listings — N(1650) .
- ↑ Particle listings — N(1675) .
- ↑ Particle listings — N(1680) .
- ↑ Particle listings — N(1700) .
- ↑ Particle listings — N(1710) .
- ↑ Particle listings — N(1720) .
- ↑ Particle listings — N(2190) .
- ↑ Particle listings — N(2220) .
- ↑ Particle listings — N(2250) .
Further reading
- Thomas, A. W.; Weise, W. (2001). The Structure of the Nucleon. Berlin, DE: Wiley-WCH. ISBN 3-527-40297-7.
- Brown, G .E.; Jackson, A. D. (1976). The Nucleon–Nucleon Interaction. North-Holland Publishing. ISBN 978-0-7204-0335-0.
- Nakamura, N. et al. (2011). "Review of Particle Physics". Journal of Physics G 37 (7): 075021. doi:10.1088/0954-3899/37/7A/075021. Bibcode: 2010JPhG...37g5021N.
 |