Quadrisecant

Short description: Line through four points of a curve

Three quadrisecants of a trefoil knot

In geometry, a quadrisecant or quadrisecant line of a space curve is a line that passes through four points of the curve. This is the largest possible number of intersections that a generic space curve can have with a line, and for such curves the quadrisecants form a discrete set of lines. Quadrisecants have been studied for curves of several types:

• Knots and links in knot theory, when nontrivial, always have quadrisecants, and the existence and number of quadrisecants has been studied in connection with knot invariants including the minimum total curvature and the ropelength of a knot.
• The number of quadrisecants of a non-singular algebraic curve in complex projective space can be computed by a formula derived by Arthur Cayley.
• Quadrisecants of arrangements of skew lines touch subsets of four lines from the arrangement. They are associated with ruled surfaces and the Schläfli double six configuration.

Definition and motivation

A quadrisecant is a line that intersects a curve, surface, or other set in four distinct points. It is analogous to a secant line, a line that intersects a curve or surface in two points; and a trisecant, a line that intersects a curve or surface in three points.

Compared to secants and trisecants, quadrisecants are especially relevant for space curves, because they have the largest possible number of intersection points of a line with a generic curve. In the plane, a generic curve can be crossed arbitrarily many times by a line; for instance, small generic perturbations of the sine curve are crossed infinitely often by the horizontal axis. In contrast, if an arbitrary space curve is perturbed by a small distance to make it generic, there will be no lines through five or more points of the perturbed curve. Nevertheless, any quadrisecants of the original space curve will remain present nearby in its perturbation. For generic space curves, the quadrisecants form a discrete set of lines. In contrast, when trisecants occur, they form continuous families of lines.

One explanation for this phenomenon is visual: looking at a space curve from far away, the space of such points of view can be described as a two-dimensional sphere, one point corresponding to each direction. Pairs of strands of the curve may appear to cross from all of these points of view, or from a two-dimensional subset of them. Three strands will form a triple crossing when the point of view lies on a trisecant, and four strands will form a quadruple crossing from a point of view on a quadrisecant. Each constraint that the crossing of a pair of strands lies on another strand reduces the number of degrees of freedom by one (for a generic curve), so the points of view on trisecants form a one-dimensional (continuously infinite) subset of the sphere, while the points of view on quadrisecants form a zero-dimensional (discrete) subset. C. T. C. Wall writes that the fact that generic space curves are crossed at most four times by lines is "one of the simplest theorems of the kind", a model case for analogous theorems on higher-dimensional transversals.

Depending on the properties of the curve, it may have no quadrisecants, finitely many, or infinitely many. These considerations make it of interest to determine conditions for the existence of quadrisecants, or to find bounds on their number in various special cases, such as knotted curves, algebraic curves, or arrangements of lines.

For special classes of curves

Knots and links

In three-dimensional Euclidean space, every nontrivial tame knot or link has a quadrisecant. Originally established in the case of knotted polygons and smooth knots by Erika Pannwitz, this result was extended to knots in suitably general position and links with nonzero linking number, and later to all nontrivial tame knots and links.

Pannwitz proved more strongly that, for a locally flat disk having the knot as its boundary, the number of singularities of the disk can be used to construct a lower bound on the number of distinct quadrisecants. The existence of at least one quadrisecant follows from the fact that any such disk must have at least one singularity. (Morton Mond) conjectured that the number of distinct quadrisecants of a given knot is always at least [math]\displaystyle{ n(n-1)/2 }[/math], where [math]\displaystyle{ n }[/math] is the crossing number of the knot. Counterexamples to this conjecture have since been discovered.

Two-component links have quadrisecants in which the points on the quadrisecant appear in alternating order between the two components, and nontrivial knots have quadrisecants in which the four points, ordered cyclically as [math]\displaystyle{ abcd }[/math] on the knot, appear in order [math]\displaystyle{ acbd }[/math] along the quadrisecant. The existence of these alternating quadrisecants can be used to derive the Fáry–Milnor theorem, a lower bound on the total curvature of a nontrivial knot. Quadrisecants have also been used to find lower bounds on the ropelength of knots.

G. T. Jin and H. S. Kim conjectured that, when a knotted curve [math]\displaystyle{ K }[/math] has finitely many quadrisecants, [math]\displaystyle{ K }[/math] can be approximated with an equivalent polygonal knot with its vertices at the points where the quadrisecants intersect [math]\displaystyle{ K }[/math], in the same order as they appear on [math]\displaystyle{ K }[/math]. However, their conjecture is false: in fact, for every knot type, there is a realization for which this construction leads to a self-intersecting polygon, and another realization where this construction produces a knot of a different type.

Unsolved problem in mathematics: Does every wild knot have infinitely many quadrisecants? (more unsolved problems in mathematics)

It has been conjectured that every wild knot has an infinite number of quadrisecants.

Algebraic curves

Arthur Cayley derived a formula for the number of quadrisecants of an algebraic curve in three-dimensional complex projective space, as a function of its degree and genus. For a curve of degree [math]\displaystyle{ d }[/math] and genus [math]\displaystyle{ g }[/math], the number of quadrisecants is [math]\displaystyle{ \frac{(d-2)(d-3)^2(d-4)}{12}-\frac{g(d^2-7d+13-g)}{2}. }[/math] This formula assumes that the given curve is non-singular; adjustments may be necessary if it has singular points.

Skew lines

The Schläfli double six

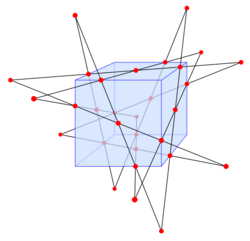
In three-dimensional Euclidean space, every set of four skew lines in general position has either two quadrisecants (also in this context called transversals) or none. Any three of the four lines determine a hyperboloid, a doubly ruled surface in which one of the two sets of ruled lines contains the three given lines, and the other ruling consists of trisecants to the given lines. If the fourth of the given lines pierces this surface, it has two points of intersection, because the hyperboloid is defined by a quadratic equation. The two trisecants of the ruled surface, through these two points, form two quadrisecants of the given four lines. On the other hand, if the fourth line is disjoint from the hyperboloid, then there are no quadrisecants. In spaces with complex number coordinates rather than real coordinates, four skew lines always have exactly two quadrisecants.

The quadrisecants of sets of lines play an important role in the construction of the Schläfli double six, a configuration of twelve lines intersecting each other in 30 crossings. If five lines [math]\displaystyle{ a_i }[/math] (for [math]\displaystyle{ i=1,2,3,4,5 }[/math]) are given in three-dimensional space, such that all five are intersected by a common line [math]\displaystyle{ b_6 }[/math] but are otherwise in general position, then each of the five quadruples of the lines [math]\displaystyle{ a_i }[/math] has a second quadrisecant [math]\displaystyle{ b_i }[/math], and the five lines [math]\displaystyle{ b_i }[/math] formed in this way are all intersected by a common line [math]\displaystyle{ a_6 }[/math]. These twelve lines and the 30 intersection points [math]\displaystyle{ a_ib_j }[/math] form the double six.

An arrangement of [math]\displaystyle{ n }[/math] complex lines with a given number of pairwise intersections and otherwise skew may be interpreted as an algebraic curve with degree [math]\displaystyle{ n }[/math] and with genus determined from its number of intersections, and Cayley's aforementioned formula used to count its quadrisecants. The same result as this formula can also be obtained by classifying the quadruples of lines by their intersections, counting the number of quadrisecants for each type of quadruple, and summing over all quadruples of lines in the given set.