Random polytope

Short description: Mathematical object

In mathematics, a random polytope is a structure commonly used in convex analysis and the analysis of linear programs in d-dimensional Euclidean space [math]\displaystyle{ \R^d }[/math]. Depending on use the construction and definition, random polytopes may differ.

Random polytope of a set of random points in accordance with definition 1

Definition

There are multiple non equivalent definitions of a Random polytope. For the following definitions. Let K be a bounded convex set in a Euclidean space:

• The convex hull of random points selected with respect to a uniform distribution inside K.
• The nonempty intersection of half-spaces in [math]\displaystyle{ \R^d }[/math].
  • The following parameterization has been used: [math]\displaystyle{ r:(\R^d \times \{0,1\})^m\rightarrow \text{Polytopes} \in \R^d }[/math] such that [math]\displaystyle{ r((p_1, 0), (p_2, 1), (p_3, 1)...(p_m, i_m)) = \{x \in \R^n: | \frac{p_j}{||p_j||} \cdot x \leq ||p_j|| \text{ if } i_j=1, \frac{p_j}{||p_j||} \cdot x \geq ||p_j|| \text{ if } i_j=0 \} }[/math] (Note: these polytopes can be empty).

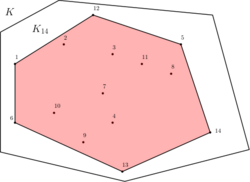
Properties definition 1

Let [math]\displaystyle{ \Kappa }[/math] be the set of convex bodies in [math]\displaystyle{ \R^d }[/math]. Assume [math]\displaystyle{ K \in\Kappa }[/math] and consider a set of uniformly distributed points [math]\displaystyle{ x_1, ..., x_n }[/math] in [math]\displaystyle{ K }[/math]. The convex hull of these points, [math]\displaystyle{ K_n }[/math], is called a random polytope inscribed in [math]\displaystyle{ K }[/math]. [math]\displaystyle{ K_n = [x_1, ..., x_n] }[/math] where the set [math]\displaystyle{ [S] }[/math] stands for the convex hull of the set. We define [math]\displaystyle{ E(k,n) }[/math] to be the expected volume of [math]\displaystyle{ K - K_n }[/math]. For a large enough [math]\displaystyle{ n }[/math] and given [math]\displaystyle{ K \in \R^n }[/math].

• vol [math]\displaystyle{ K(\frac{1}{n})\ll E(K,n) \ll }[/math] vol [math]\displaystyle{ K(\frac{1}{n}) }[/math]
  • Note: One can determine the volume of the wet part to obtain the order of the magnitude of [math]\displaystyle{ E(K,n) }[/math], instead of determining [math]\displaystyle{ E(K,n) }[/math].
• For the unit ball [math]\displaystyle{ B^d \in \R^d }[/math], the wet part [math]\displaystyle{ B^d(v \leq t) }[/math] is the annulus [math]\displaystyle{ \frac{B^d}{(1-h)B^d} }[/math] where h is of order [math]\displaystyle{ t^{\frac{2}{d+1}} }[/math]: [math]\displaystyle{ E(B^d,n) \approx }[/math] vol [math]\displaystyle{ B^d (\frac{1}{n}) \approx n^{\frac{-2}{d+1}} }[/math]

Given we have [math]\displaystyle{ V = V(x_1,...,x_d) }[/math] is the volume of a smaller cap cut off from [math]\displaystyle{ K }[/math] by aff[math]\displaystyle{ (x_1,...,x_d) }[/math], and [math]\displaystyle{ F=[x_1,...,x_d] }[/math] is a facet if and only if [math]\displaystyle{ x_{d+1},...,x_n }[/math] are all on one side of aff [math]\displaystyle{ \{x_1,...,x_d\} }[/math].

• [math]\displaystyle{ E_{\phi}(K_n) = {{n}\choose{d}} \int_K ... \int_K [(1-V)^{n-d} + V^{n-d}]\phi(F)dx_1...dx_d }[/math].
  • Note: If [math]\displaystyle{ \phi = f_{d-1} }[/math] (a function that returns the amount of d-1 dimensional faces), then [math]\displaystyle{ \phi(F) = 1 }[/math] and formula can be evaluated for smooth convex sets and for polygons in the plane.

Properties definition 2

Assume we are given a multivariate probability distribution on [math]\displaystyle{ (\R^d \times \{ 0, 1\})^m=(p_1\times i_1,\dots,p_m\times i_m)^m }[/math] that is

1. Absolutely continuous on [math]\displaystyle{ (p_1,\dots,p_d) }[/math] with respect to Lebesgue measure.
2. Generates either 0 or 1 for the [math]\displaystyle{ i }[/math]s with probability of [math]\displaystyle{ \frac{1}{2} }[/math] each.
3. Assigns a measure of 0 to the set of elements in [math]\displaystyle{ (\R^d \times \{ 0, 1\})^m }[/math] that correspond to empty polytopes.

Given this distribution, and our assumptions, the following properties hold:

• A formula is derived for the expected number of [math]\displaystyle{ k }[/math] dimensional faces on a polytope in [math]\displaystyle{ \R^d }[/math] with [math]\displaystyle{ m }[/math] constraints: [math]\displaystyle{ E_k(m) = 2^{d-k} \sum_{i = d - k}^{d}{{i}\choose{d-k}}{{m}\choose{i}}/\sum_{i=0}^{d}{{m}\choose{i}} }[/math]. (Note: [math]\displaystyle{ \lim_{m \to \infty}E_k(m) = {{d}\choose{d-k}}2^{d-k} }[/math] where [math]\displaystyle{ m\gt d }[/math]). The upper bound, or worst case, for the number of vertices with [math]\displaystyle{ m }[/math] constraints is much larger: [math]\displaystyle{ V_{max} = {m-[\frac{1}{2}(d+1)]\choose m-d} + {m-[\frac{1}{2}(d+2)]\choose m-d} }[/math].
• The probability that a new constraint is redundant is: [math]\displaystyle{ \pi_{m} = 1 - \frac{2\sum_{i=0}^{d-1}{{m-1}\choose i}}{\sum_{i=0}^{d}{m\choose i}} }[/math]. (Note: [math]\displaystyle{ \lim_{m \to \infty}{\pi_m} = 1 }[/math], and as we add more constraints, the probability a new constraint is redundant approaches 100%).
• The expected number of non-redundant constraints is: [math]\displaystyle{ C_d(m) = \frac{2m\sum_{i=0}^{d-1}{{m-1}\choose i}}{\sum_{i=0}^{d}{{m}\choose i}} }[/math]. (Note: [math]\displaystyle{ \lim_{m \to \infty}C_d(m) = 2d }[/math]).

Example uses

• Minimal caps
• Macbeath regions
• Approximations (approximations of convex bodies see properties of definition 1)
• Economic cap covering theorem (see relation from properties of definition 1 to floating bodies)