Scale-invariant feature operator

Short description: Algorithm to detect local features in images

In the fields of computer vision and image analysis, the scale-invariant feature operator (or SFOP) is an algorithm to detect local features in images. The algorithm was published by Förstner et al. in 2009.

Algorithm

The scale-invariant feature operator (SFOP) is based on two theoretical concepts:

• spiral model
• feature operator

Desired properties of keypoint detectors:

• Invariance and repeatability for object recognition
• Accuracy to support camera calibration
• Interpretability: Especially corners and circles, should be part of the detected keypoints (see figure).
• As few control parameters as possible with clear semantics
• Complementarity to known detectors

scale-invariant corner/circle detector.

Theory

Maximize the weight

Maximize the weight [math]\displaystyle{ w }[/math]= 1/variance of a point [math]\displaystyle{ p }[/math]

[math]\displaystyle{ w(\mathbf{p},\alpha,\tau,\sigma)=\left(N(\sigma)-2\right)\frac{\lambda_{min}(M(\mathbf{p},\alpha,\tau,\sigma))}{\Omega(\mathbf{p},\alpha,\tau,\sigma)}    }[/math]  

comprising:

1. the image model

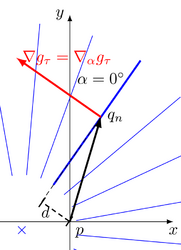
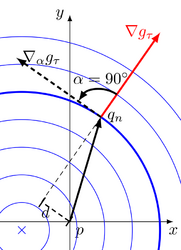
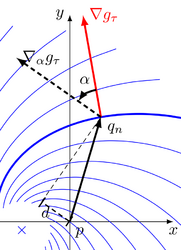
• Distance d of an edge from a reference point p in a spiral feature
• 
• 
• 

[math]\displaystyle{ \begin{align} \Omega(\mathbf{p},\alpha,\tau,\sigma)& =\sum_{n=1}^{N(\sigma)}[(\mathbf{q}_n-\mathbf{p})^T \mathbf{R}_{\alpha}\mathbf{\nabla}_T g(\mathbf{q}_n)]^2G_{\sigma}(\mathbf{q}_n-\mathbf{p}) \\ & =N(\sigma)\mathbf{tr}\left\{R_{\alpha}\mathbf{\nabla}_{\tau}\mathbf{\nabla}_{\tau}^TR_{\alpha}^T*\mathbf{p}\mathbf{p}^TG_{\sigma}(\mathbf{p})\right\} \end{align} }[/math]

2. the smaller eigenvalue of the structure tensor [math]\displaystyle{ \underbrace{M(\mathbf{p},\alpha,\tau,\sigma)}_{\text{structure tensor}}=\underbrace{G_{\sigma}(\mathbf{p})}_{\text{weighted summation}}*\underbrace{(R_{\sigma}\nabla_{\tau}\nabla_{\tau}^TR_{\sigma}^T)}_{\text{squared rotated gradients}} }[/math]

Reduce the search space

Reduce the 5-dimensional search space by

• linking the differentiation scale [math]\displaystyle{ \tau }[/math] to the integration scale

[math]\displaystyle{ \tau=\sigma/3 }[/math]

• solving for the optimal [math]\displaystyle{ \hat \alpha }[/math] using the model

[math]\displaystyle{ \Omega(\alpha) = a - b \cos(2 \alpha - 2 \alpha_0) }[/math]

• and determining the parameters from three angles, e. g.

[math]\displaystyle{ \Omega(0^\circ), \Omega(60^\circ), \Omega(120^\circ)\quad \rightarrow \quad a, b, \alpha_0 \quad \rightarrow \quad \hat\alpha }[/math]

• pre-selection possible:

[math]\displaystyle{ \alpha = 0^\circ \, \rightarrow \, \mbox{junctions}, \quad \alpha = 90^\circ \, \rightarrow \, \mbox{circular features} }[/math]

Filter potential keypoints

• non-maxima suppression over scale, space and angle

• thresholding the isotropy [math]\displaystyle{ \lambda_{2(M)} }[/math]:
  eigenvalues characterize the shape of the keypoint, smallest eigenvalue has to be larger than threshold [math]\displaystyle{ T_{\lambda} }[/math]
  derived from noise variance [math]\displaystyle{ V(n) }[/math] and significance level [math]\displaystyle{ S }[/math]:

[math]\displaystyle{ T_\lambda(V(n), \tau, \sigma, S) = \frac{N(\sigma)}{16 \pi \tau^4} V(n) \chi^2_{2,S} }[/math]

Algorithm

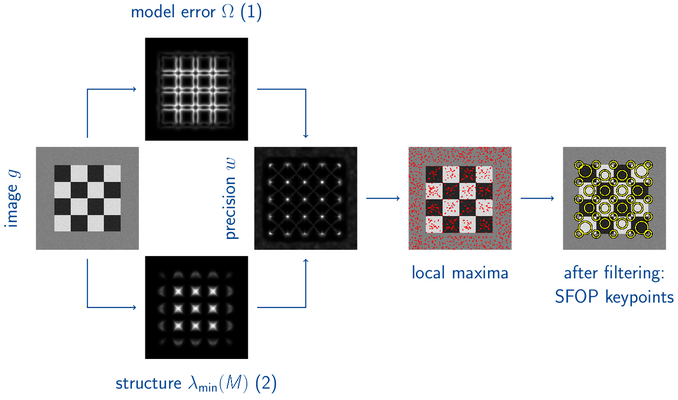
Results

Interpretability of SFOP keypoints

• Results of different detectors on a Siemens star
• 

  Sfop: junctions red, circular features cyan

• 

  Edge-based Regions

• 

  Intensity-based Regions

• 

  MSER

• 

  Harris affine

• 

  Hessian affine

• 

  Lowe

See also

• Corner detection
• Feature detection (computer vision)

External links

• Project website at University of Bonn