Signed graph

From HandWiki
Short description: Graph with sign-labeled edges
There are eight ways that signs can be assigned to the sides of a triangle. An odd number of negative signs makes an unbalanced triangle, according to Fritz Heider's theory.

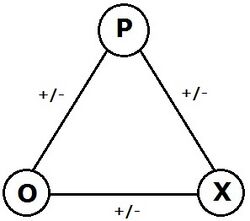
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.

A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953.[1] Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group.[2] At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs.[3][4]

Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas.[5] For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are a natural context for questions about odd and even cycles in graphs. They appear in computing the ground state energy in the non-ferromagnetic Ising model; for this one needs to find a largest balanced edge set in Σ. They have been applied to data classification in correlation clustering.

Fundamental theorem

The sign of a path is the product of the signs of its edges. Thus a path is positive only if there are an even number of negative edges in it (where zero is even). In the mathematical balance theory of Frank Harary, a signed graph is balanced when every cycle is positive. Harary proves that a signed graph is balanced when (1) for every pair of nodes, all paths between them have the same sign, or (2) the vertices partition into a pair of subsets (possibly empty), each containing only positive edges, but connected by negative edges.[1] It generalizes the theorem that an ordinary (unsigned) graph is bipartite if and only if every cycle has even length.

A simple proof uses the method of switching. Switching a signed graph means reversing the signs of all edges between a vertex subset and its complement. To prove Harary's theorem, one shows by induction that Σ can be switched to be all positive if and only if it is balanced.

A weaker theorem, but with a simpler proof, is that if every 3-cycle in a signed complete graph is positive, then the graph is balanced. For the proof, pick an arbitrary node n and place it and all those nodes that are linked to n by a positive edge in one group, called A, and all those linked to n by a negative edge in the other, called B. Since this is a complete graph, every two nodes in A must be friends and every two nodes in B must be friends, otherwise there would be a 3-cycle which was unbalanced. (Since this is a complete graph, any one negative edge would cause an unbalanced 3-cycle.) Likewise, all negative edges must go between the two groups.[6]

Frustration

Frustration index

The frustration index (early called the line index of balance[7]) of Σ is the smallest number of edges whose deletion, or equivalently whose sign reversal (a theorem of Harary[7]), makes Σ balanced. The reason for the equivalence is that the frustration index equals the smallest number of edges whose negation (or, equivalently, deletion; makes Σ balanced.

A second way of describing the frustration index is that it is the smallest number of edges that cover all negative cycles. This quantity has been called the negative cycle cover number.

There is another equivalent definition (which can be proved easily by switching). Give each vertex a value of +1 or −1; we call this a state of Σ. An edge is called satisfied if it is positive and both endpoints have the same value, or it is negative and the endpoints have opposite values. An edge that is not satisfied is called frustrated. The smallest number of frustrated edges over all states is the frustration index. This definition was first introduced in a different notation by Abelson and Rosenberg under the (obsolete) name complexity.[8] The complement of such a set is a balanced subgraph of Σ with the most possible edges.

Finding the frustration index is an NP-hard problem. Aref et al. suggest binary programming models that are capable of computing the frustration index of graphs with up to 105 edges in a reasonable time.[9][10] [11] One can see the NP-hard complexity by observing that the frustration index of an all-negative signed graph is the same as the maximum cut problem in graph theory, which is NP-hard.

The frustration index is important in a model of spin glasses, the mixed Ising model. In this model, the signed graph is fixed. A state consists of giving a "spin", either "up" or "down", to each vertex. We think of spin up as +1 and spin down as −1. Thus, each state has a number of frustrated edges. The energy of a state is larger when it has more frustrated edges, so a ground state is a state with the fewest frustrated energy. Thus, to find the ground state energy of Σ one has to find the frustration index.

Frustration number

The analogous vertex number is the frustration number, defined as the smallest number of vertices whose deletion from Σ results in balance. Equivalently, one wants the largest order of a balanced induced subgraph of Σ.

Algorithmic problems

Three fundamental questions about a signed graph are: Is it balanced? What is the largest size of a balanced edge set in it? What is the smallest number of vertices that must be deleted to make it balanced? The first question is easy to solve in polynomial time. The second question is called the Frustration Index or Maximum Balanced Subgraph problem. It is NP-hard because its special case (when all edges of the graph are negative) is the NP-hard problem Maximum Cut. The third question is called the Frustration Number or Maximum Balanced Induced Subgraph problem, is also NP-hard; see e.g.[12]

Matroid theory

There are two matroids associated with a signed graph, called the signed-graphic matroid (also called the frame matroid or sometimes bias matroid) and the lift matroid, both of which generalize the cycle matroid of a graph. They are special cases of the same matroids of a biased graph.

The frame matroid (or signed-graphic matroid) M(G) has for its ground set the edge set E.[13] An edge set is independent if each component contains either no circles or just one circle, which is negative. (In matroid theory a half-edge acts exactly like a negative loop.) A circuit of the matroid is either a positive circle, or a pair of negative circles together with a connecting simple path, such that the two circles are either disjoint (then the connecting path has one end in common with each circle and is otherwise disjoint from both) or share just a single common vertex (in this case the connecting path is that single vertex). The rank of an edge set S is n − b, where n is the number of vertices of G and b is the number of balanced components of S, counting isolated vertices as balanced components. This matroid is the column matroid of the incidence matrix of the signed graph. That is why it describes the linear dependencies of the roots of a classical root system.

The extended lift matroid L0(G) has for its ground set the set E0 the union of edge set E with an extra point, which we denote e0. The lift matroid L(G) is the extended lift matroid restricted to E. The extra point acts exactly like a negative loop, so we describe only the lift matroid. An edge set is independent if it contains either no circles or just one circle, which is negative. (This is the same rule that is applied separately to each component in the signed-graphic matroid.) A matroid circuit is either a positive circle or a pair of negative circles that are either disjoint or have just a common vertex. The rank of an edge set S is n − c + ε, where c is the number of components of S, counting isolated vertices, and ε is 0 if S is balanced and 1 if it is not.

Other kinds of "signed graph"

Sometimes the signs are taken to be +1 and −1. This is only a difference of notation, if the signs are still multiplied around a circle and the sign of the product is the important thing. However, there are two other ways of treating the edge labels that do not fit into signed graph theory.

The term signed graph is applied occasionally to graphs in which each edge has a weight, w(e) = +1 or −1. These are not the same kind of signed graph; they are weighted graphs with a restricted weight set. The difference is that weights are added, not multiplied. The problems and methods are completely different.

The name is also applied to graphs in which the signs function as colors on the edges. The significance of the color is that it determines various weights applied to the edge, and not that its sign is intrinsically significant. This is the case in knot theory, where the only significance of the signs is that they can be interchanged by the two-element group, but there is no intrinsic difference between positive and negative. The matroid of a sign-colored graph is the cycle matroid of the underlying graph; it is not the frame or lift matroid of the signed graph. The sign labels, instead of changing the matroid, become signs on the elements of the matroid.

In this article we discuss only signed graph theory in the strict sense. For sign-colored graphs see colored matroids.

Signed digraph

A signed digraph is a directed graph with signed arcs. Signed digraphs are far more complicated than signed graphs, because only the signs of directed cycles are significant. For instance, there are several definitions of balance, each of which is hard to characterize, in strong contrast with the situation for signed undirected graphs.

Signed digraphs should not be confused with oriented signed graphs. The latter are bidirected graphs, not directed graphs (except in the trivial case of all positive signs).

Vertex signs

A vertex-signed graph, sometimes called a marked graph, is a graph whose vertices are given signs. A circle is called consistent (but this is unrelated to logical consistency) or harmonious if the product of its vertex signs is positive, and inconsistent or inharmonious if the product is negative. There is no simple characterization of harmonious vertex-signed graphs analogous to Harary's balance theorem; instead, the characterization has been a difficult problem, best solved (even more generally) by Joglekar, Shah, and Diwan (2012).[14]

It is often easy to add edge signs to the theory of vertex signs without major change; thus, many results for vertex-signed graphs (or "marked signed graphs") extend naturally to vertex-and-edge-signed graphs. This is notably true for the characterization of harmony by Joglekar, Shah, and Diwan (2012).

The difference between a marked signed graph and a signed graph with a state function (as in § Frustration) is that the vertex signs in the former are part of the essential structure, while a state function is a variable function on the signed graph.

Note that the term "marked graph" is widely used in Petri nets in a completely different meaning; see the article on marked graphs.

Coloring

As with unsigned graphs, there is a notion of signed graph coloring. Where a coloring of a graph is a mapping from the vertex set to the natural numbers, a coloring of a signed graph is a mapping from the vertex set to the integers. The constraints on proper colorings come from the edges of the signed graph. The integers assigned to two vertices must be distinct if they are connected by a positive edge. The labels on adjacent vertices must not be additive inverses if the vertices are connected by a negative edge. There can be no proper coloring of a signed graph with a positive loop.

When restricting the vertex labels to the set of integers with magnitude at most a natural number k, the set of proper colorings of a signed graph is finite. The relation between the number of such proper colorings and k is a polynomial in k; when expressed in terms of [math]\displaystyle{ 2k+1 }[/math] it is called the chromatic polynomial of the signed graph. It is analogous to the chromatic polynomial of an unsigned graph.

Applications

Social psychology

In social psychology, signed graphs have been used to model social situations, with positive edges representing friendships and negative edges enmities between nodes, which represent people.[3] Then, for example, a positive 3-cycle is either three mutual friends, or two friends with a common enemy; while a negative 3-cycle is either three mutual enemies, or two enemies who share a mutual friend. According to balance theory, positive cycles are balanced and supposed to be stable social situations, whereas negative cycles are unbalanced and supposed to be unstable. According to the theory, in the case of three mutual enemies, this is because sharing a common enemy is likely to cause two of the enemies to become friends. In the case of two enemies sharing a friend, the shared friend is likely to choose one over the other and turn one of his or her friendships into an enemy.

Antal, Krapivsky and Reder consider social dynamics as the change in sign on an edge of a signed graph.[15] The social relations with previous friends of a divorcing couple are used to illustrate the evolution of a signed graph in society. Another illustration describes the changing international alliances between European powers in the decades before the First World War. They consider local triad dynamics and constrained triad dynamics, where in the latter case a relationship change is made only when the total number of unbalanced triads is reduced. The simulation presumed a complete graph with random relations having a random unbalanced triad selected for transformation. The evolution of the signed graph with N nodes under this process is studied and simulated to describe the stationary density of friendly links.

Balance theory has been severely challenged, especially in its application to large systems, on the theoretical ground that friendly relations tie a society together, while a society divided into two camps of enemies would be highly unstable.[16] Experimental studies have also provided only weak confirmation of the predictions of structural balance theory.[17]

Spin glasses

In physics, signed graphs are a natural context for the nonferromagnetic Ising model, which is applied to the study of spin glasses.

Complex systems

A three-variable signed digraph representing a simple trophic system

Using an analytic method initially developed in population biology and ecology, but now used in many scientific disciplines, signed digraphs have found application in reasoning about the behavior of complex causal systems.[18][19] Such analyses answer questions about feedback at given levels of the system, and about the direction of variable responses given a perturbation to a system at one or more points, variable correlations given such perturbations, the distribution of variance across the system, and the sensitivity or insensitivity of particular variables to system perturbations.

Data clustering

Correlation clustering looks for natural clustering of data by similarity. The data points are represented as the vertices of a graph, with a positive edge joining similar items and a negative edge joining dissimilar items.

Neuroscience

Brain can be considered as a signed graph where synchrony and anti-synchrony between activity patterns of brain regions determine positive and negative edges. In this regard, stability and energy of the brain network can be explored.[20] Also, recently, the concept of frustration has been used in brain network analysis to identify the non-trivial assemblage of neural connections and highlight the adjustable elements of the brain.[21]

Generalizations

A signed graph is the special kind of gain graph in which the gain group has order 2. The pair (G, B(Σ)) determined by a signed graph Σ is a special kind of biased graph. The sign group has the special property, not shared by larger gain groups, that the edge signs are determined up to switching by the set B(Σ) of balanced cycles.[22]

Notes

  1. ↑ 1.0 1.1 Harary, Frank (1955), "On the notion of balance of a signed graph", Michigan Mathematical Journal 2: 143–146, http://projecteuclid.org/getRecord?id=euclid.mmj/1028989917 
  2. ↑ Kőnig, Dénes (1936), Akademische Verlagsgesellschaft, ed., Theorie der endlichen und unendlichen Graphen 
  3. ↑ 3.0 3.1 Cartwright, D.; Harary, Frank (1956). "Structural balance: a generalization of Heider's theory". Psychological Review 63 (5): 277–293. doi:10.1037/h0046049. PMID 13359597. https://snap.stanford.edu/class/cs224w-readings/cartwright56balance.pdf. 
  4. ↑ Steven Strogatz (2010), The enemy of my enemy, The New York Times , February 14, 2010
  5. ↑ Zaslavsky, Thomas (1998), "A mathematical bibliography of signed and gain graphs and allied areas", Electronic Journal of Combinatorics 5: Dynamic Surveys 8, 124 pp., http://www.combinatorics.org/ojs/index.php/eljc/article/view/DS8 .
  6. ↑ Luis Von Ahn Science of the Web Lecture 3 p. 28
  7. ↑ 7.0 7.1 Harary, Frank (1959), On the measurement of structural balance, Behavioral Science 4, 316–323.
  8. ↑ Robert P. Abelson; Milton J. Rosenberg (1958), Symbolic psycho-logic: a model of attitudinal cognition, Behavioral Science 3, 1–13.
  9. ↑ Aref, Samin; Mason, Andrew J.; Wilson, Mark C. (2019). "A Modelling and Computational Study of the Frustration Index in Signed Networks". arXiv:1611.09030 [cs.SI].
  10. ↑ Aref, Samin; Mason, Andrew J.; Wilson, Mark C. (2018), Goldengorin, Boris, ed., "Computing the Line Index of Balance Using Integer Programming Optimisation" (in en), Optimization Problems in Graph Theory: In Honor of Gregory Z. Gutin's 60th Birthday, Springer Optimization and Its Applications (Springer International Publishing): pp. 65–84, doi:10.1007/978-3-319-94830-0_3, ISBN 9783319948300 
  11. ↑ Aref, Samin; Wilson, Mark C (2019-04-01). Estrada, Ernesto. ed. "Balance and frustration in signed networks" (in en). Journal of Complex Networks 7 (2): 163–189. doi:10.1093/comnet/cny015. ISSN 2051-1329. 
  12. ↑ Gülpinar, N.; Gutin, G.; Mitra, G.; Zverovitch, A. (2004). "Extracting pure network submatrices in linear programs using signed graphs". Discrete Appl. Math. 137 (3): 359–372. doi:10.1016/S0166-218X(03)00361-5. 
  13. ↑ Zaslavsky, Thomas (1982), "Signed graphs", Discrete Applied Mathematics 4 (1): 47–74, doi:10.1016/0166-218X(82)90033-6 . Erratum. Discrete Applied Mathematics, 5 (1983), 248
  14. ↑ Manas Joglekar, Nisarg Shah, and Ajit A. Diwan (2012), "Balanced group labeled graphs", Discrete Mathematics, vol. 312, no. 9, pp. 1542–1549.
  15. ↑ T. Antal, P.L. Krapivsky & S. Redner (2006) Social Balance on Networks: The Dynamics of Friendship and Enmity
  16. ↑ B. Anderson, in Perspectives on Social Network Research, ed. P.W. Holland and S. Leinhardt. New York: Academic Press, 1979.
  17. ↑ Morrissette, Julian O.; Jahnke, John C. (1967). "No relations and relations of strength zero in the theory of structural balance". Human Relations 20 (2): 189–195. doi:10.1177/001872676702000207. 
  18. ↑ Puccia, Charles J. and Levins, Richard (1986). Qualitative Modeling of Complex Systems: An Introduction to Loop Analysis and Time Averaging. Harvard University Press, Cambridge, MA.
  19. ↑ Dambacher, Jeffrey M.; Li, Hiram W.; Rossignol, Philippe A. (2002). "Relevance of community structure in assessing indeterminacy of ecological predictions". Ecology 83 (5): 1372–1385. doi:10.1890/0012-9658(2002)083[1372:rocsia2.0.co;2]. 
  20. ↑ "Topological impact of negative links on the stability of resting-state brain network". Scientific Reports 11 (1): 2176. January 2021. doi:10.1038/s41598-021-81767-7. PMID 33500525. Bibcode: 2021NatSR..11.2176S. 
  21. ↑ "Pattern of frustration formation in the functional brain network". Network Neuroscience 6 (4): 1334-1356. October 2022. doi:10.1162/netn_a_00268. https://direct.mit.edu/netn/article/6/4/1334/112207/Pattern-of-frustration-formation-in-the-functional. 
  22. ↑ "Characterizations of signed graphs". Journal of Graph Theory 5 (4): 401–406. 1981. doi:10.1002/jgt.3190050409. 

References



Retrieved from "https://handwiki.org/wiki/index.php?title=Signed_graph&oldid=3008325"