Small retrosnub icosicosidodecahedron
| Small retrosnub icosicosidodecahedron | |
|---|---|

| |
| Type | Uniform star polyhedron |
| Elements | F = 112, E = 180 V = 60 (χ = −8) |
| Faces by sides | (40+60){3}+12{5/2} |
| Wythoff symbol | | 3/2 3/2 5/2 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U72, C91, W118 |
| Dual polyhedron | Small hexagrammic hexecontahedron |
| Vertex figure |  (35.5/3)/2 |
| Bowers acronym | Sirsid |
File:Small retrosnub icosicosidodecahedron.stl
In geometry, the small retrosnub icosicosidodecahedron (also known as a retrosnub disicosidodecahedron, small inverted retrosnub icosicosidodecahedron, or retroholosnub icosahedron) is a nonconvex uniform polyhedron, indexed as U72. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices.[1] It is given a Schläfli symbol sr{⁵/₃,³/₂}.
The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries.
George Olshevsky nicknamed it the yog-sothoth (after the Cthulhu Mythos deity).[2][3]
Convex hull
Its convex hull is a nonuniform truncated dodecahedron.
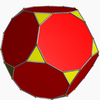 Truncated dodecahedron |
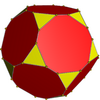 Convex hull |
 Small retrosnub icosicosidodecahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a small retrosnub icosicosidodecahedron are all the even permutations of [math]\displaystyle{ \begin{array}{crrrc} \Bigl(& \pm \bigl[1-\varphi-\alpha\bigr],& 0\,,& \pm \bigl[3-\varphi\alpha\bigr] &\Bigr), \\ \Bigl(& \pm \bigl[\varphi-1-\alpha\bigr],& \pm\,2\,,& \pm \bigl[2\varphi-1-\varphi\alpha\bigr] &\Bigr), \\ \Bigl(& \pm \bigl[\varphi+1-\alpha\bigr],& \pm\,2\bigl[\varphi-1\bigr],& \pm \bigl[1-\varphi\alpha\bigr] &\Bigr), \end{array} }[/math] where [math]\displaystyle{ \varphi = \tfrac{1+\sqrt 5}{2} }[/math] is the golden ratio and [math]\displaystyle{ \alpha = \sqrt{3\varphi-2}. }[/math]
See also
References
- ↑ Maeder, Roman. "72: small retrosnub icosicosidodecahedron". https://www.mathconsult.ch/static/unipoly/72.html.
- ↑ Birrell, Robert J. (May 1992). The Yog-sothoth: analysis and construction of the small inverted retrosnub icosicosidodecahedron (M.S.). California State University.
- ↑ Bowers, Jonathan (2000). "Uniform Polychora". in Reza Sarhagi. Bridges Conference. pp. 239–246. https://archive.bridgesmathart.org/2000/bridges2000-239.pdf.
External links
- Weisstein, Eric W.. "Small retrosnub icosicosidodecahedron". http://mathworld.wolfram.com/SmallRetrosnubIcosicosidodecahedron.html.
- Klitzing, Richard. "3D star small retrosnub icosicosidodecahedron". https://bendwavy.org/klitzing/dimensions/../incmats/sirsid.htm.
 |

