Tanc function

In mathematics, the tanc function is defined for $z\ne 0$ as $$\mathrm{tanc}(z)=\frac{\tan (z)}{z}$$

Tanc 2D plot

Tanc'(z) 2D plot

Tanc integral 2D plot

Tanc integral 3D plot

Properties

The first-order derivative of the tanc function is given by

$\frac{{\sec }^2(z)}{z}-\frac{\tan (z)}{z^2}$

The Taylor series expansion is$$\mathrm{tanc}z\approx (1+\frac{1}{3}{z}^2+\frac{2}{15}{z}^4+\frac{17}{315}{z}^6+\frac{62}{2835}{z}^8+\frac{1382}{155925}{z}^{10}+\frac{21844}{6081075}{z}^{12}+\frac{929569}{638512875}{z}^{14}+O(z^{16}))$$which leads to the series expansion of the integral as$$\underset{0}{\overset{z}{\int }}\frac{\tan (x)}{x}dx=(z+\frac{1}{9}{z}^3+\frac{2}{75}{z}^5+\frac{17}{2205}{z}^7+\frac{62}{25515}{z}^9+\frac{1382}{1715175}{z}^{11}+\frac{21844}{79053975}{z}^{13}+\frac{929569}{9577693125}{z}^{15}+O(z^{17}))$$The Padé approximant is$$\mathrm{tanc}\left(z\right)=(1-\frac{7}{51}{z}^2+\frac{1}{255}{z}^4-\frac{2}{69615}{z}^6+\frac{1}{34459425}{z}^8){(1-\frac{8}{17}{z}^2+\frac{7}{255}{z}^4-\frac{4}{9945}{z}^6+\frac{1}{765765}{z}^8)}^{-1}$$

In terms of other special functions

• $\mathrm{tanc}(z)=\frac{2i\mathrm{K}\mathrm{u}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{M}(1,2,2iz)}{(2z+\pi )\mathrm{K}\mathrm{u}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{M}(1,2,i(2z+\pi ))}$, where $\mathrm{K}\mathrm{u}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{M}(a,b,z)$ is Kummer's confluent hypergeometric function.
• $\mathrm{tanc}(z)=\frac{2i\mathrm{HeunB}(2,0,0,0,\sqrt{2}\sqrt{iz})}{(2z+\pi )\mathrm{HeunB}(2,0,0,0,\sqrt{2}\sqrt{(i/2)(2z+\pi )})}$, where $\mathrm{H}\mathrm{e}\mathrm{u}\mathrm{n}\mathrm{B}(q,\alpha ,\gamma ,\delta ,ϵ,z)$ is the biconfluent Heun function.
• $\mathrm{tanc}(z)=\frac{\mathrm{W}\mathrm{h}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{a}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{M}(0,1/2,2iz)}{\mathrm{W}\mathrm{h}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{a}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{M}(0,1/2,i(2z+\pi ))z}$, where $\mathrm{W}\mathrm{h}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{a}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{M}(a,b,z)$ is a Whittaker function.

Gallery

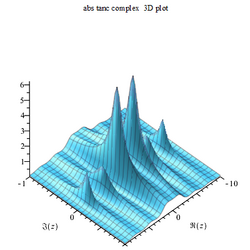Tanc abs complex 3D

Tanc Im complex 3D plot

Tanc Re complex 3D plot

See also

• Sinhc function
• Tanhc function
• Coshc function