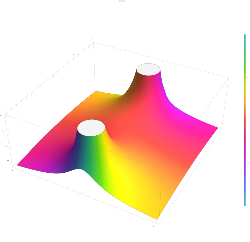
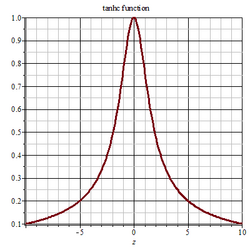
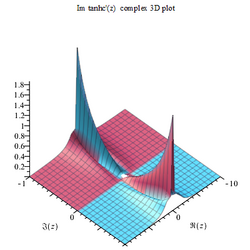
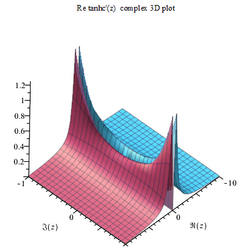
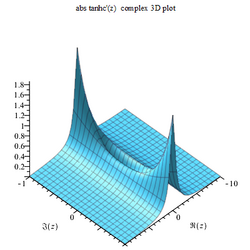
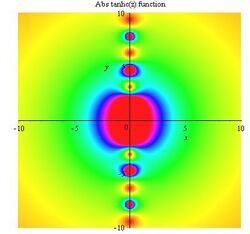
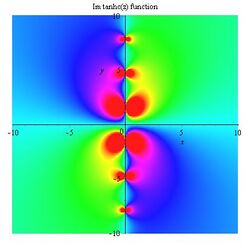
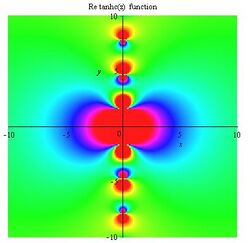
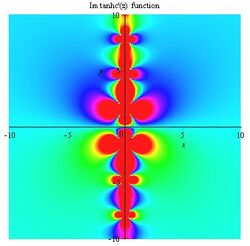
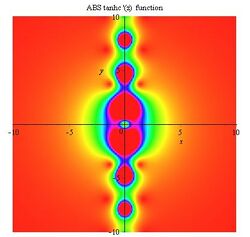
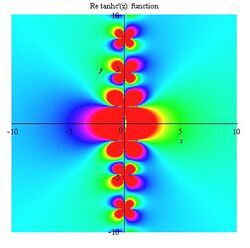
Tanhc function

In mathematics, the tanhc function is defined for $z \neq 0$ as^[1] $tanhc (z) = \frac{\tanh (z)}{z}$ The tanhc function is the hyperbolic analogue of the tanc function.

Properties

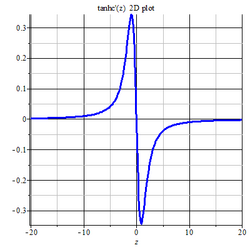
The first-order derivative is given by

\frac{{sech}^{2} (z)}{z} - \frac{\tanh (z)}{z^{2}}

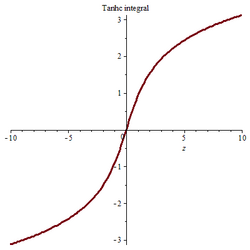
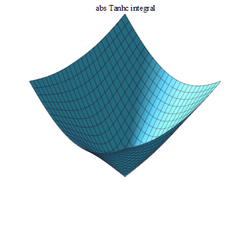
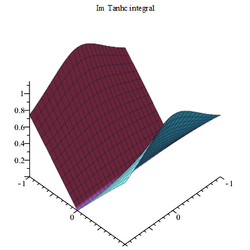
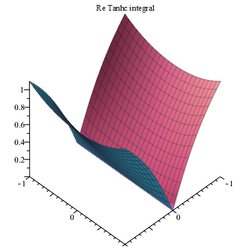
The Taylor series expansion $tanhc z \approx (1 - \frac{1}{3} z^{2} + \frac{2}{15} z^{4} - \frac{17}{315} z^{6} + \frac{62}{2835} z^{8} - \frac{1382}{155925} z^{10} + \frac{21844}{6081075} z^{12} - \frac{929569}{638512875} z^{14} + O (z^{16}))$ which leads to the series expansion of the integral as $\int_{0}^{z} \frac{\tanh (x)}{x} d x = (z - \frac{1}{9} z^{3} + \frac{2}{75} z^{5} - \frac{17}{2205} z^{7} + \frac{62}{25515} z^{9} - \frac{1382}{1715175} z^{11} + O (z^{13}))$

The Padé approximant is $tanhc (z) = (1 + \frac{7}{51} z^{2} + \frac{1}{255} z^{4} + \frac{2}{69615} z^{6} + \frac{1}{34459425} z^{8}) {(1 + \frac{8}{17} z^{2} + \frac{7}{255} z^{4} + \frac{4}{9945} z^{6} + \frac{1}{765765} z^{8})}^{- 1}$

In terms of other special functions

$tanhc (z) = 2 \frac{K u m m e r M (1, 2, 2 z)}{(2 i z + π) K u m m e r M (1, 2, i π - 2 z) e^{2 z - 1 / 2 i π}}$ , where $K u m m e r M (a, b, z)$ is Kummer's confluent hypergeometric function.
$tanhc (z) = 2 \frac{HeunB (2, 0, 0, 0, \sqrt{2} \sqrt{z})}{(2 i z + π) HeunB (2, 0, 0, 0, \sqrt{2} \sqrt{1 / 2 i π - z}) e^{2 z - 1 / 2 i π}}$ , where $H e u n B (q, α, γ, δ, ϵ, z)$ is the biconfluent Heun function.
$tanhc (z) = \frac{i W h i t t a k e r M (0, 1 / 2, 2 z)}{W h i t t a k e r M (0, 1 / 2, i π - 2 z)} z$ , where $W h i t t a k e r M (a, b, z)$ is a Whittaker function.