Tangent cone

Short description: Generalization of the tangent space to a manifold to the case of certain spaces

In geometry, the tangent cone is a generalization of the notion of the tangent space to a manifold to the case of certain spaces with singularities.

Definitions in nonlinear analysis

In nonlinear analysis, there are many definitions for a tangent cone, including the adjacent cone, Bouligand's contingent cone, and the Clarke tangent cone. These three cones coincide for a convex set, but they can differ on more general sets.

Clarke tangent cone

Let [math]\displaystyle{ A }[/math] be a nonempty closed subset of the Banach space [math]\displaystyle{ X }[/math]. The Clarke's tangent cone to [math]\displaystyle{ A }[/math] at [math]\displaystyle{ x_0\in A }[/math], denoted by [math]\displaystyle{ \widehat{T}_A(x_0) }[/math] consists of all vectors [math]\displaystyle{ v\in X }[/math], such that for any sequence [math]\displaystyle{ \{t_n\}_{n\ge 1}\subset\mathbb{R} }[/math] tending to zero, and any sequence [math]\displaystyle{ \{x_n\}_{n\ge 1}\subset A }[/math] tending to [math]\displaystyle{ x_0 }[/math], there exists a sequence [math]\displaystyle{ \{v_n\}_{n\ge 1}\subset X }[/math] tending to [math]\displaystyle{ v }[/math], such that for all [math]\displaystyle{ n\ge 1 }[/math] holds [math]\displaystyle{ x_n+t_nv_n\in A }[/math]

Clarke's tangent cone is always subset of the corresponding contingent cone (and coincides with it, when the set in question is convex). It has the important property of being a closed convex cone.

Definition in convex geometry

Let K be a closed convex subset of a real vector space V and ∂K be the boundary of K. The solid tangent cone to K at a point x ∈ ∂K is the closure of the cone formed by all half-lines (or rays) emanating from x and intersecting K in at least one point y distinct from x. It is a convex cone in V and can also be defined as the intersection of the closed half-spaces of V containing K and bounded by the supporting hyperplanes of K at x. The boundary T_K of the solid tangent cone is the tangent cone to K and ∂K at x. If this is an affine subspace of V then the point x is called a smooth point of ∂K and ∂K is said to be differentiable at x and T_K is the ordinary tangent space to ∂K at x.

Definition in algebraic geometry

y² = x³ + x² (red) with tangent cone (blue)

Let X be an affine algebraic variety embedded into the affine space [math]\displaystyle{ k^n }[/math], with defining ideal [math]\displaystyle{ I\subset k[x_1,\ldots ,x_n] }[/math]. For any polynomial f, let [math]\displaystyle{ \operatorname{in}(f) }[/math] be the homogeneous component of f of the lowest degree, the initial term of f, and let

[math]\displaystyle{ \operatorname{in}(I)\subset k[x_1,\ldots ,x_n] }[/math]

be the homogeneous ideal which is formed by the initial terms [math]\displaystyle{ \operatorname{in}(f) }[/math] for all [math]\displaystyle{ f \in I }[/math], the initial ideal of I. The tangent cone to X at the origin is the Zariski closed subset of [math]\displaystyle{ k^n }[/math] defined by the ideal [math]\displaystyle{ \operatorname{in}(I) }[/math]. By shifting the coordinate system, this definition extends to an arbitrary point of [math]\displaystyle{ k^n }[/math] in place of the origin. The tangent cone serves as the extension of the notion of the tangent space to X at a regular point, where X most closely resembles a differentiable manifold, to all of X. (The tangent cone at a point of [math]\displaystyle{ k^n }[/math] that is not contained in X is empty.)

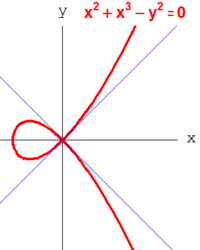
For example, the nodal curve

[math]\displaystyle{ C: y^2=x^3+x^2 }[/math]

is singular at the origin, because both partial derivatives of f(x, y) = y² − x³ − x² vanish at (0, 0). Thus the Zariski tangent space to C at the origin is the whole plane, and has higher dimension than the curve itself (two versus one). On the other hand, the tangent cone is the union of the tangent lines to the two branches of C at the origin,

[math]\displaystyle{ x=y,\quad x=-y. }[/math]

Its defining ideal is the principal ideal of k[x] generated by the initial term of f, namely y² − x² = 0.

The definition of the tangent cone can be extended to abstract algebraic varieties, and even to general Noetherian schemes. Let X be an algebraic variety, x a point of X, and (O_X,x, m) be the local ring of X at x. Then the tangent cone to X at x is the spectrum of the associated graded ring of O_X,x with respect to the m-adic filtration:

[math]\displaystyle{ \operatorname{gr}_m O_{X,x}=\bigoplus_{i\geq 0} m^i / m^{i+1}. }[/math]

If we look at our previous example, then we can see that graded pieces contain the same information. So let

[math]\displaystyle{ (\mathcal{O}_{X,x},\mathfrak{m}) = \left(\left(\frac{k[x,y]}{(y^2 - x^3 - x^2)}\right)_{(x,y)}, (x,y)\right) }[/math]

then if we expand out the associated graded ring

[math]\displaystyle{ \begin{align} \operatorname{gr}_m O_{X,x} &= \frac{\mathcal{O}_{X,x}}{(x,y)} \oplus \frac{(x,y)}{(x,y)^2} \oplus \frac{(x,y)^2}{(x,y)^3} \oplus \cdots \\ &= k \oplus \frac{(x,y)}{(x,y)^2} \oplus \frac{(x,y)^2}{(x,y)^3} \oplus \cdots \end{align} }[/math]

we can see that the polynomial defining our variety

[math]\displaystyle{ y^2 - x^3 - x^2 \equiv y^2 - x^2 }[/math] in [math]\displaystyle{ \frac{(x,y)^2}{(x,y)^3} }[/math]

See also

• Cone
• Monge cone
• Normal cone

References

• Hazewinkel, Michiel, ed. (2001), "Tangent cone", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=T/t092120 
• "Tangent Cones". Set-Valued Analysis. Modern Birkhäuser Classics. Birkhäuser. 2009. pp. 117–177. doi:10.1007/978-0-8176-4848-0_4. ISBN 978-0-8176-4848-0.