The Petersen Graph
 | |
| Author |
|
|---|---|
| Series | Australian Mathematical Society Lecture Series |
| Subject | The Petersen graph |
| Publisher | Cambridge University Press |
Publication date | 1993 |
The Petersen Graph is a mathematics book about the Petersen graph and its applications in graph theory. It was written by Derek Holton and John Sheehan, and published in 1993 by the Cambridge University Press as volume 7 in their Australian Mathematical Society Lecture Series.
Topics
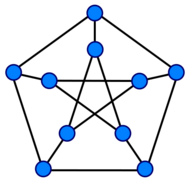
The Petersen graph is an undirected graph with ten vertices and fifteen edges, commonly drawn as a pentagram within a pentagon, with corresponding vertices attached to each other. It has many unusual mathematical properties, and has frequently been used as a counterexample to conjectures in graph theory.[1][2] The book uses these properties as an excuse to cover several advanced topics in graph theory where this graph plays an important role.[1][3] It is heavily illustrated, and includes both open problems on the topics it discusses and detailed references to the literature on these problems.[1][4]
After an introductory chapter, the second and third chapters concern graph coloring, the history of the four color theorem for planar graphs, its equivalence to 3-edge-coloring of planar cubic graphs, the snarks (cubic graphs that have no such colorings), and the conjecture of W. T. Tutte that every snark has the Petersen graph as a graph minor. Two more chapters concern closely related topics, perfect matchings (the sets of edges that can have a single color in a 3-edge-coloring) and nowhere-zero flows (the dual concept to planar graph coloring). The Petersen graph shows up again in another conjecture of Tutte, that when a bridgeless graph does not have the Petersen graph as a minor, it must have a nowhere-zero 4-flow.[3]
Chapter six of the book concerns cages, the smallest regular graphs with no cycles shorter than a given length. The Petersen graph is an example: it is the smallest 3-regular graph with no cycles of length shorter than 5. Chapter seven is on hypohamiltonian graphs, the graphs that do not have a Hamiltonian cycle through all vertices but that do have cycles through every set of all but one vertices; the Petersen graph is the smallest example. The next chapter concerns the symmetries of graphs, and types of graphs defined by their symmetries, including the distance-transitive graphs and strongly regular graphs (of which the Petersen graph is an example)[3] and the Cayley graphs (of which it is not).[1] The book concludes with a final chapter of miscellaneous topics too small for their own chapters.[3]
Audience and reception
The book assumes that its readers already have some familiarity with graph theory.[3] It can be used as a reference work for researchers in this area,[1][2] or as the basis of an advanced course in graph theory.[2][3]
Although Carsten Thomassen describes the book as "elegant",[4] and Robin Wilson evaluates its exposition as "generally good",[2] reviewer Charles H. C. Little takes the opposite view, finding fault with its copyediting, with some of its mathematical notation, and with its failure to discuss the lattice of integer combinations of perfect matchings, in which the number of copies of the Petersen graph in the "bricks" of a certain graph decomposition plays a key role in computing the dimension.[1] Reviewer Ian Anderson notes the superficiality of some of its coverage, but concludes that the book "succeeds in giving an exciting and enthusiastic glimpse" of graph theory.[3]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Little, Charles H. C. (1994), "Review of The Petersen Graph", Mathematical Reviews
- ↑ 2.0 2.1 2.2 2.3 "Review of The Petersen Graph", Bulletin of the London Mathematical Society 27 (1): 89, January 1995, doi:10.1112/blms/27.1.89
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Anderson, Ian (March 1995), "Review of The Petersen Graph", The Mathematical Gazette 79 (484): 239–240, doi:10.2307/3620120
- ↑ 4.0 4.1 "Review of The Petersen Graph", zbMATH
 |
