Truncated icosidodecahedron

Short description: Archimedean solid

Truncated icosidodecahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 62, E = 180, V = 120 (χ = 2)
Faces by sides	30{4}+20{6}+12{10}
Conway notation	bD or taD
Schläfli symbols	tr{5,3} or [math]\displaystyle{ t\begin{Bmatrix} 5 \\ 3 \end{Bmatrix} }[/math]
	t0,1,2{5,3}
Wythoff symbol	2 3 5 |
Coxeter diagram
Symmetry group	Ih, H3, [5,3], (*532), order 120
Rotation group	I, [5,3]+, (532), order 60
Dihedral angle	6-10: 142.62° 4-10: 148.28° 4-6: 159.095°
References	U28, C31, W16
Properties	Semiregular convex zonohedron
Colored faces	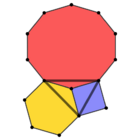4.6.10 (Vertex figure)
Disdyakis triacontahedron (dual polyhedron)	Net

In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

It has 62 faces: 30 squares, 20 regular hexagons, and 12 regular decagons. It has the most edges and vertices of all Platonic and Archimedean solids, though the snub dodecahedron has more faces. Of all vertex-transitive polyhedra, it occupies the largest percentage (89.80%) of the volume of a sphere in which it is inscribed, very narrowly beating the snub dodecahedron (89.63%) and small rhombicosidodecahedron (89.23%), and less narrowly beating the truncated icosahedron (86.74%); it also has by far the greatest volume (206.8 cubic units) when its edge length equals 1. Of all vertex-transitive polyhedra that are not prisms or antiprisms, it has the largest sum of angles (90 + 120 + 144 = 354 degrees) at each vertex; only a prism or antiprism with more than 60 sides would have a larger sum. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated icosidodecahedron is a 15-zonohedron.

Names

The name truncated icosidodecahedron, given originally by Johannes Kepler, is misleading. An actual truncation of an icosidodecahedron has rectangles instead of squares. This nonuniform polyhedron is topologically equivalent to the Archimedean solid. Alternate interchangeable names are: Truncated icosidodecahedron (Johannes Kepler) Rhombitruncated icosidodecahedron (Magnus Wenninger) Great rhombicosidodecahedron (Robert Williams, Peter Cromwell) Omnitruncated dodecahedron or icosahedron (Norman Johnson)

Icosidodecahedron and its truncation

The name great rhombicosidodecahedron refers to the relationship with the (small) rhombicosidodecahedron (compare section Dissection).
There is a nonconvex uniform polyhedron with a similar name, the nonconvex great rhombicosidodecahedron.

Area and volume

The surface area A and the volume V of the truncated icosidodecahedron of edge length a are:

[math]\displaystyle{ \begin{align} A &= 30 \left (1 + \sqrt{3} + \sqrt{5 + 2\sqrt{5}} \right)a^2 &&\approx 174.292\,0303a^2. \\ V &= \left( 95 + 50\sqrt{5} \right) a^3 &&\approx 206.803\,399a^3. \end{align} }[/math]

If a set of all 13 Archimedean solids were constructed with all edge lengths equal, the truncated icosidodecahedron would be the largest.

Cartesian coordinates

Cartesian coordinates for the vertices of a truncated icosidodecahedron with edge length 2φ − 2, centered at the origin, are all the even permutations of:

(±1/φ, ±1/φ, ±(3 + φ)),

(±2/φ, ±φ, ±(1 + 2φ)),

(±1/φ, ±φ², ±(−1 + 3φ)),

(±(2φ − 1), ±2, ±(2 + φ)) and

(±φ, ±3, ±2φ),

where φ = 1 + √5/2 is the golden ratio.

Dissection

The truncated icosidodecahedron is the convex hull of a rhombicosidodecahedron with cuboids above its 30 squares, whose height to base ratio is φ. The rest of its space can be dissected into nonuniform cupolas, namely 12 between inner pentagons and outer decagons and 20 between inner triangles and outer hexagons.

An alternative dissection also has a rhombicosidodecahedral core. It has 12 pentagonal rotundae between inner pentagons and outer decagons. The remaining part is a toroidal polyhedron.

dissection images
These images show the rhombicosidodecahedron (violet) and the truncated icosidodecahedron (green). If their edge lengths are 1, the distance between corresponding squares is φ. The toroidal polyhedron remaining after the core and twelve rotundae are cut out

Orthogonal projections

The truncated icosidodecahedron has seven special orthogonal projections, centered on a vertex, on three types of edges, and three types of faces: square, hexagonal and decagonal. The last two correspond to the A₂ and H₂ Coxeter planes.

Orthogonal projections

Centered by	Vertex	Edge 4-6	Edge 4-10	Edge 6-10	Face square	Face hexagon	Face decagon
Solid
Wireframe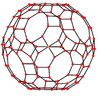
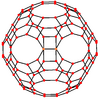
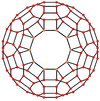
Projective symmetry	[2]+	[2]	[2]	[2]	[2]	[6]	[10]
Dual image

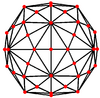
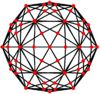
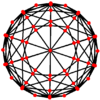
Spherical tilings and Schlegel diagrams

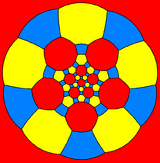
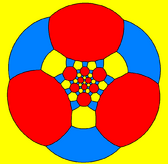
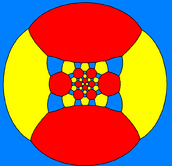
The truncated icosidodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Schlegel diagrams are similar, with a perspective projection and straight edges.

Orthographic projection	Stereographic projections
	Decagon-centered	Hexagon-centered	Square-centered

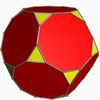
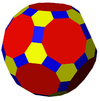
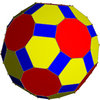
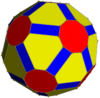
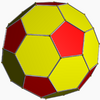
Geometric variations

Within Icosahedral symmetry there are unlimited geometric variations of the truncated icosidodecahedron with isogonal faces. The truncated dodecahedron, rhombicosidodecahedron, and truncated icosahedron as degenerate limiting cases.

Truncated icosidodecahedral graph

Truncated icosidodecahedral graph
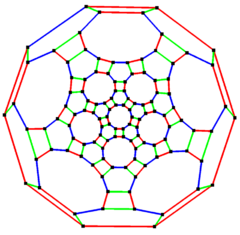5-fold symmetry
Vertices	120
Edges	180
Radius	15
Diameter	15
Girth	4
Automorphisms	120 (A5×2)
Chromatic number	2
Properties	Cubic, Hamiltonian, regular, zero-symmetric
Table of graphs and parameters

In the mathematical field of graph theory, a truncated icosidodecahedral graph (or great rhombicosidodecahedral graph) is the graph of vertices and edges of the truncated icosidodecahedron, one of the Archimedean solids. It has 120 vertices and 180 edges, and is a zero-symmetric and cubic Archimedean graph.

Schlegel diagram graphs

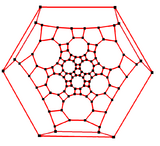3-fold symmetry

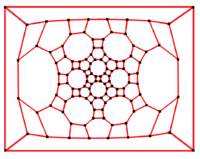2-fold symmetry

Related polyhedra and tilings

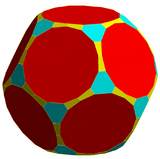
Bowtie icosahedron and dodecahedron contain two trapezoidal faces in place of the square.

This polyhedron can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

References

• Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5 
• Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2. 
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. 
• Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999).
• Eric W. Weisstein, GreatRhombicosidodecahedron (Archimedean solid) at MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra x3x5x - grid". https://bendwavy.org/klitzing/dimensions/polyhedra.htm. 

External links

• Weisstein, Eric W.. "Great rhombicosidodecahedron". http://mathworld.wolfram.com/GreatRhombicosidodecahedron.html. 
• * Weisstein, Eric W.. "Great rhombicosidodecahedral graph". http://mathworld.wolfram.com/GreatRhombicosidodecahedralGraph.html. 
• Editable printable net of a truncated icosidodecahedron with interactive 3D view
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra