Waterman polyhedron
 | This article needs additional citations for verification. (April 2023) (Learn how and when to remove this template message) |
In geometry, the Waterman polyhedra are a family of polyhedra discovered around 1990 by the mathematician Steve Waterman. A Waterman polyhedron is created by packing spheres according to the cubic close(st) packing (CCP), also known as the face-centered cubic (fcc) packing, then sweeping away the spheres that are farther from the center than a defined radius,[1] then creating the convex hull of the sphere centers.
Cubic Close(st) Packed spheres with radius √24
Corresponding Waterman polyhedron W24 Origin 1
Waterman polyhedra form a vast family of polyhedra. Some of them have a number of nice properties such as multiple symmetries, or interesting and regular shapes. Others are just a collection of faces formed from irregular convex polygons.
The most popular Waterman polyhedra are those with centers at the point (0,0,0) and built out of hundreds of polygons. Such polyhedra resemble spheres. In fact, the more faces a Waterman polyhedron has, the more it resembles its circumscribed sphere in volume and total area.
With each point of 3D space we can associate a family of Waterman polyhedra with different values of radii of the circumscribed spheres. Therefore, from a mathematical point of view we can consider Waterman polyhedra as 4D spaces W(x, y, z, r), where x, y, z are coordinates of a point in 3D, and r is a positive number greater than 1.[2]
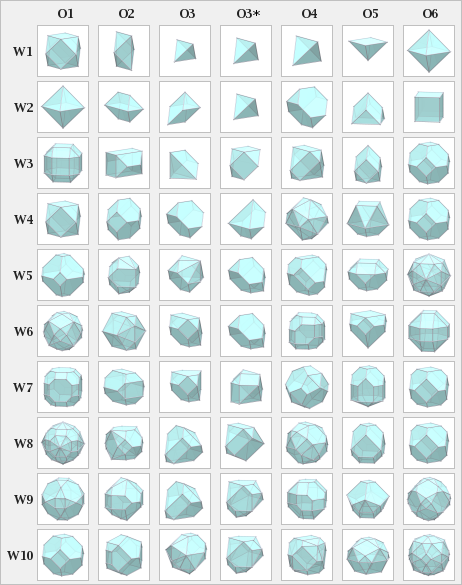
Seven origins of cubic close(st) packing (CCP)
There can be seven origins defined in CCP,[3] where n = {1, 2, 3, …}:
- Origin 1: offset 0,0,0, radius [math]\displaystyle{ \sqrt{2n} }[/math]
- Origin 2: offset 1/2,1/2,0, radius [math]\displaystyle{ \tfrac12\sqrt{2+4n} }[/math]
- Origin 3: offset 1/3,1/3,2/3, radius [math]\displaystyle{ \tfrac13\sqrt{6(n+1)} }[/math]
- Origin 3*: offset 1/3,1/3,1/3, radius [math]\displaystyle{ \tfrac13\sqrt{3+6n} }[/math]
- Origin 4: offset 1/2,1/2,1/2, radius [math]\displaystyle{ \tfrac12\sqrt{3+8(n-1)} }[/math]
- Origin 5: offset 0,0,1/2, radius [math]\displaystyle{ \tfrac12\sqrt{1+4n} }[/math]
- Origin 6: offset 1,0,0, radius [math]\displaystyle{ \sqrt{1+2(n-1)} }[/math]
Depending on the origin of the sweeping, a different shape and resulting polyhedron are obtained.
Relation to Platonic and Archimedean solids
| This section does not cite any external source. HandWiki requires at least one external source. See citing external sources. (April 2023) (Learn how and when to remove this template message) |
Some Waterman polyhedra create Platonic solids and Archimedean solids. For this comparison of Waterman polyhedra they are normalized, e.g. W2 O1 has a different size or volume than W1 O6, but has the same form as an octahedron.[citation needed]
Platonic solids
- Tetrahedron: W1 O3*, W2 O3*, W1 O3, W1 O4
- Octahedron: W2 O1, W1 O6
- Cube: W2 O6
- Icosahedron and dodecahedron have no representation as Waterman polyhedra.[citation needed]
Archimedean solids
- Cuboctahedron: W1 O1, W4 O1
- Truncated octahedron: W10 O1
- Truncated tetrahedron: W4 O3, W2 O4
- The other Archimedean solids have no representation as Waterman polyhedra.[citation needed]
The W7 O1 might be mistaken for a truncated cuboctahedron, as well W3 O1 = W12 O1 mistaken for a rhombicuboctahedron, but those Waterman polyhedra have two edge lengths and therefore do not qualify as Archimedean solids.[citation needed]
Generalized Waterman polyhedra
| This section does not cite any external source. HandWiki requires at least one external source. See citing external sources. (April 2023) (Learn how and when to remove this template message) |
Generalized Waterman polyhedra are defined as the convex hull derived from the point set of any spherical extraction from a regular lattice.[citation needed]
Included is a detailed analysis of the following 10 lattices – bcc, cuboctahedron, diamond, fcc, hcp, truncated octahedron, rhombic dodecahedron, simple cubic, truncated tet tet, truncated tet truncated octahedron cuboctahedron.[citation needed]
Each of the 10 lattices were examined to isolate those particular origin points that manifested a unique polyhedron, as well as possessing some minimal symmetry requirement.[citation needed] From a viable origin point, within a lattice, there exists an unlimited series of polyhedra.[citation needed] Given its proper sweep interval, then there is a one-to-one correspondence between each integer value and a generalized Waterman polyhedron.[citation needed]
Notes
- ↑ Popko, Edward S. (2012). Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press. pp. 174–177. ISBN 9781466504295.
- ↑ Visualizing Waterman Polyhedra with MuPAD by M. Majewski
- ↑ 7 Origins of CCP Waterman polyhedra by Mark Newbold
External links
- Steve Waterman's Homepage
- Waterman Polyhedra Java applet by Mark Newbold
- Maurice Starck's write-up
- hand-made models by Magnus Wenninger
- write-up by Paul Bourke
- on-line generator by Paul Bourke
- program to make Waterman polyhedron by Adrian Rossiter in Antiprism
- Waterman projection and write up by Carlos Furiti
- rotating globe by Izidor Hafner
- real time winds and temperature on Waterman projection by Cameron Beccario
- Solar Termination (Waterman) by Mike Bostock
- interactive Waterman butterfly map by Jason Davies
- write-up by Maurice Starck
- first 1000 Waterman polyhedra and sphere clusters by Nemo Thorx
- OEIS sequence A119870 (Number of vertices of the root-n Waterman polyhedron)
- Steve Waterman's Waterman polyhedron (WP)
- Generalized Waterman polyhedron by Ed Pegg jr of Wolfram
- various Waterman sphere clusters by Ed Pegg jr of Wolfram
- app to make 4d waterman polyhedron in Great Stella by Rob Webb
- Waterman polyhedron app in Matlab needs a workaround as shown on the following reference page
- Waterman polyhedron in Mupad
 |  |
