Heap (data structure)

From HandWiki
Short description: Computer science data structure
Example of a binary max-heap with node keys being integers between 1 and 100

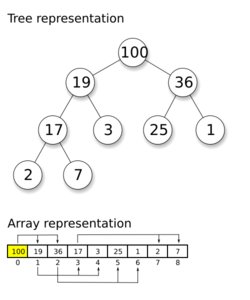
In computer science, a heap is a tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C.[1] The node at the "top" of the heap (with no parents) is called the root node.

The heap is one maximally efficient implementation of an abstract data type called a priority queue, and in fact, priority queues are often referred to as "heaps", regardless of how they may be implemented. In a heap, the highest (or lowest) priority element is always stored at the root. However, a heap is not a sorted structure; it can be regarded as being partially ordered. A heap is a useful data structure when it is necessary to repeatedly remove the object with the highest (or lowest) priority, or when insertions need to be interspersed with removals of the root node.

A common implementation of a heap is the binary heap, in which the tree is an complete[2] binary tree (see figure). The heap data structure, specifically the binary heap, was introduced by J. W. J. Williams in 1964, as a data structure for the heapsort sorting algorithm.[3] Heaps are also crucial in several efficient graph algorithms such as Dijkstra's algorithm. When a heap is a complete binary tree, it has the smallest possible height—a heap with N nodes and a branches for each node always has loga N height.

Note that, as shown in the graphic, there is no implied ordering between siblings or cousins and no implied sequence for an in-order traversal (as there would be in, e.g., a binary search tree). The heap relation mentioned above applies only between nodes and their parents, grandparents, etc. The maximum number of children each node can have depends on the type of heap.

Heaps are typically constructed in-place in the same array where the elements are stored, with their structure being implicit in the access pattern of the operations. Heaps differ in this way from other data structures with similar or in some cases better theoretic bounds such as Radix trees in that they require no additional memory beyond that used for storing the keys.

Operations

The common operations involving heaps are:

Basic
  • find-max (or find-min): find a maximum item of a max-heap, or a minimum item of a min-heap, respectively (a.k.a. peek)
  • insert: adding a new key to the heap (a.k.a., push[4])
  • extract-max (or extract-min): returns the node of maximum value from a max heap [or minimum value from a min heap] after removing it from the heap (a.k.a., pop[5])
  • delete-max (or delete-min): removing the root node of a max heap (or min heap), respectively
  • replace: pop root and push a new key. This is more efficient than a pop followed by a push, since it only needs to balance once, not twice, and is appropriate for fixed-size heaps.[6]
Creation
  • create-heap: create an empty heap
  • heapify: create a heap out of given array of elements
  • merge (union): joining two heaps to form a valid new heap containing all the elements of both, preserving the original heaps.
  • meld: joining two heaps to form a valid new heap containing all the elements of both, destroying the original heaps.
Inspection
  • size: return the number of items in the heap.
  • is-empty: return true if the heap is empty, false otherwise.
Internal
  • increase-key or decrease-key: updating a key within a max- or min-heap, respectively
  • delete: delete an arbitrary node (followed by moving last node and sifting to maintain heap)
  • sift-up: move a node up in the tree, as long as needed; used to restore heap condition after insertion. Called "sift" because node moves up the tree until it reaches the correct level, as in a sieve.
  • sift-down: move a node down in the tree, similar to sift-up; used to restore heap condition after deletion or replacement.

Implementation

Heaps are usually implemented with an array, as follows:

  • Each element in the array represents a node of the heap, and
  • The parent / child relationship is defined implicitly by the elements' indices in the array.
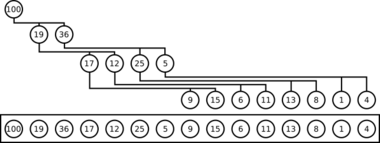
Example of a complete binary max-heap with node keys being integers from 1 to 100 and how it would be stored in an array.

For a binary heap, in the array, the first index contains the root element. The next two indices of the array contain the root's children. The next four indices contain the four children of the root's two child nodes, and so on. Therefore, given a node at index i, its children are at indices [math]\displaystyle{ 2i + 1 }[/math] and [math]\displaystyle{ 2i + 2 }[/math], and its parent is at index ⌊(i−1)/2⌋. This simple indexing scheme makes it efficient to move "up" or "down" the tree.

Balancing a heap is done by sift-up or sift-down operations (swapping elements which are out of order). As we can build a heap from an array without requiring extra memory (for the nodes, for example), heapsort can be used to sort an array in-place.

After an element is inserted into or deleted from a heap, the heap property may be violated, and the heap must be re-balanced by swapping elements within the array.

Although different type of heaps implement the operations differently, the most common way is as follows:

  • Insertion: Add the new element at the end of the heap, in the first available free space. If this will violate the heap property, sift up the new element (swim operation) until the heap property has been reestablished.
  • Extraction: Remove the root and insert the last element of the heap in the root. If this will violate the heap property, sift down the new root (sink operation) to reestablish the heap property.
  • Replacement: Remove the root and put the new element in the root and sift down. When compared to extraction followed by insertion, this avoids a sift up step.

Construction of a binary (or d-ary) heap out of a given array of elements may be performed in linear time using the classic Floyd algorithm, with the worst-case number of comparisons equal to 2N − 2s2(N) − e2(N) (for a binary heap), where s2(N) is the sum of all digits of the binary representation of N and e2(N) is the exponent of 2 in the prime factorization of N.[7] This is faster than a sequence of consecutive insertions into an originally empty heap, which is log-linear.[lower-alpha 1]

Variants


Comparison of theoretic bounds for variants

Here are time complexities[8] of various heap data structures. Function names assume a min-heap. For the meaning of "O(f)" and "Θ(f)" see Big O notation.

Operation find-min delete-min insert decrease-key meld
Binary[8] Θ(1) Θ(log n) O(log n) O(log n) Θ(n)
Leftist Θ(1) Θ(log n) Θ(log n) O(log n) Θ(log n)
Binomial[8][9] Θ(1) Θ(log n) Θ(1)[lower-alpha 2] Θ(log n) O(log n)[lower-alpha 3]
Fibonacci[8][10] Θ(1) O(log n)[lower-alpha 2] Θ(1) Θ(1)[lower-alpha 2] Θ(1)
Pairing[11] Θ(1) O(log n)[lower-alpha 2] Θ(1) o(log n)[lower-alpha 2][lower-alpha 4] Θ(1)
Brodal[14][lower-alpha 5] Θ(1) O(log n) Θ(1) Θ(1) Θ(1)
Rank-pairing[16] Θ(1) O(log n)[lower-alpha 2] Θ(1) Θ(1)[lower-alpha 2] Θ(1)
Strict Fibonacci[17] Θ(1) O(log n) Θ(1) Θ(1) Θ(1)
2-3 heap[18] O(log n) O(log n)[lower-alpha 2] O(log n)[lower-alpha 2] Θ(1) ?
  1. ↑ Each insertion takes O(log(k)) in the existing size of the heap, thus [math]\displaystyle{ \sum_{k=1}^n O(\log k) }[/math]. Since [math]\displaystyle{ \log n/2 = (\log n) - 1 }[/math], a constant factor (half) of these insertions are within a constant factor of the maximum, so asymptotically we can assume [math]\displaystyle{ k = n }[/math]; formally the time is [math]\displaystyle{ n O(\log n) - O(n) = O(n \log n) }[/math]. This can also be readily seen from Stirling's approximation.
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 Amortized time.
  3. ↑ n is the size of the larger heap.
  4. ↑ Lower bound of [math]\displaystyle{ \Omega(\log\log n), }[/math][12] upper bound of [math]\displaystyle{ O(2^{2\sqrt{\log\log n}}). }[/math][13]
  5. ↑ Brodal and Okasaki later describe a persistent variant with the same bounds except for decrease-key, which is not supported. Heaps with n elements can be constructed bottom-up in O(n).[15]

Applications

The heap data structure has many applications.

  • Heapsort: One of the best sorting methods being in-place and with no quadratic worst-case scenarios.
  • Selection algorithms: A heap allows access to the min or max element in constant time, and other selections (such as median or kth-element) can be done in sub-linear time on data that is in a heap.[19]
  • Graph algorithms: By using heaps as internal traversal data structures, run time will be reduced by polynomial order. Examples of such problems are Prim's minimal-spanning-tree algorithm and Dijkstra's shortest-path algorithm.
  • Priority queue: A priority queue is an abstract concept like "a list" or "a map"; just as a list can be implemented with a linked list or an array, a priority queue can be implemented with a heap or a variety of other methods.
  • K-way merge: A heap data structure is useful to merge many already-sorted input streams into a single sorted output stream. Examples of the need for merging include external sorting and streaming results from distributed data such as a log structured merge tree. The inner loop is obtaining the min element, replacing with the next element for the corresponding input stream, then doing a sift-down heap operation. (Alternatively the replace function.) (Using extract-max and insert functions of a priority queue are much less efficient.)

Programming language implementations

  • The C++ Standard Library provides the make_heap, push_heap and pop_heap algorithms for heaps (usually implemented as binary heaps), which operate on arbitrary random access iterators. It treats the iterators as a reference to an array, and uses the array-to-heap conversion. It also provides the container adaptor priority_queue, which wraps these facilities in a container-like class. However, there is no standard support for the replace, sift-up/sift-down, or decrease/increase-key operations.
  • The Boost C++ libraries include a heaps library. Unlike the STL, it supports decrease and increase operations, and supports additional types of heap: specifically, it supports d-ary, binomial, Fibonacci, pairing and skew heaps.
  • There is a generic heap implementation for C and C++ with D-ary heap and B-heap support. It provides an STL-like API.
  • The standard library of the D programming language includes std.container.BinaryHeap, which is implemented in terms of D's ranges. Instances can be constructed from any random-access range. BinaryHeap exposes an input range interface that allows iteration with D's built-in foreach statements and integration with the range-based API of the std.algorithm package.
  • For Haskell there is the Data.Heap module.
  • The Java platform (since version 1.5) provides a binary heap implementation with the class java.util.PriorityQueue in the Java Collections Framework. This class implements by default a min-heap; to implement a max-heap, programmer should write a custom comparator. There is no support for the replace, sift-up/sift-down, or decrease/increase-key operations.
  • Python has a heapq module that implements a priority queue using a binary heap. The library exposes a heapreplace function to support k-way merging.
  • PHP has both max-heap (SplMaxHeap) and min-heap (SplMinHeap) as of version 5.3 in the Standard PHP Library.
  • Perl has implementations of binary, binomial, and Fibonacci heaps in the Heap distribution available on CPAN.
  • The Go language contains a heap package with heap algorithms that operate on an arbitrary type that satisfies a given interface. That package does not support the replace, sift-up/sift-down, or decrease/increase-key operations.
  • Apple's Core Foundation library contains a CFBinaryHeap structure.
  • Pharo has an implementation of a heap in the Collections-Sequenceable package along with a set of test cases. A heap is used in the implementation of the timer event loop.
  • The Rust programming language has a binary max-heap implementation, BinaryHeap, in the collections module of its standard library.
  • .NET has PriorityQueue class which uses quaternary (d-ary) min-heap implementation. It is available from .NET 6.

See also

References

  1. ↑ Black (ed.), Paul E. (2004-12-14). Entry for heap in Dictionary of Algorithms and Data Structures. Online version. U.S. National Institute of Standards and Technology, 14 December 2004. Retrieved on 2017-10-08 from https://xlinux.nist.gov/dads/HTML/heap.html.
  2. ↑ CORMEN, THOMAS H. (2009). INTRODUCTION TO ALGORITHMS. United States of America: The MIT Press Cambridge, Massachusetts London, England. pp. 151–152. ISBN 978-0-262-03384-8. 
  3. ↑ Williams, J. W. J. (1964), "Algorithm 232 - Heapsort", Communications of the ACM 7 (6): 347–348, doi:10.1145/512274.512284 
  4. ↑ The Python Standard Library, 8.4. heapq — Heap queue algorithm, heapq.heappush
  5. ↑ The Python Standard Library, 8.4. heapq — Heap queue algorithm, heapq.heappop
  6. ↑ The Python Standard Library, 8.4. heapq — Heap queue algorithm, heapq.heapreplace
  7. ↑ Suchenek, Marek A. (2012), "Elementary Yet Precise Worst-Case Analysis of Floyd's Heap-Construction Program", Fundamenta Informaticae (IOS Press) 120 (1): 75–92, doi:10.3233/FI-2012-751 .
  8. ↑ 8.0 8.1 8.2 8.3 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. (1990). Introduction to Algorithms (1st ed.). MIT Press and McGraw-Hill. ISBN 0-262-03141-8. 
  9. ↑ "Binomial Heap | Brilliant Math & Science Wiki" (in en-us). https://brilliant.org/wiki/binomial-heap/. 
  10. ↑ Fredman, Michael Lawrence; Tarjan, Robert E. (July 1987). "Fibonacci heaps and their uses in improved network optimization algorithms". Journal of the Association for Computing Machinery 34 (3): 596-615. doi:10.1145/28869.28874. http://bioinfo.ict.ac.cn/~dbu/AlgorithmCourses/Lectures/Fibonacci-Heap-Tarjan.pdf. 
  11. ↑ Iacono, John (2000), "Improved upper bounds for pairing heaps", Proc. 7th Scandinavian Workshop on Algorithm Theory, Lecture Notes in Computer Science, 1851, Springer-Verlag, pp. 63–77, doi:10.1007/3-540-44985-X_5, ISBN 3-540-67690-2, http://john2.poly.edu/papers/swat00/paper.pdf 
  12. ↑ Fredman, Michael Lawrence (July 1999). "On the Efficiency of Pairing Heaps and Related Data Structures". Journal of the Association for Computing Machinery 46 (4): 473–501. doi:10.1145/320211.320214. http://www.uqac.ca/azinflou/Fichiers840/EfficiencyPairingHeap.pdf. 
  13. ↑ Pettie, Seth (2005). "Towards a Final Analysis of Pairing Heaps". FOCS '05 Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science. pp. 174–183. doi:10.1109/SFCS.2005.75. ISBN 0-7695-2468-0. http://web.eecs.umich.edu/~pettie/papers/focs05.pdf. 
  14. ↑ Brodal, Gerth S. (1996), "Worst-Case Efficient Priority Queues", Proc. 7th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 52–58, http://www.cs.au.dk/~gerth/papers/soda96.pdf 
  15. ↑ Goodrich, Michael T.; Tamassia, Roberto (2004). "7.3.6. Bottom-Up Heap Construction". Data Structures and Algorithms in Java (3rd ed.). pp. 338-341. ISBN 0-471-46983-1. 
  16. ↑ Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (November 2011). "Rank-pairing heaps". SIAM J. Computing 40 (6): 1463–1485. doi:10.1137/100785351. http://sidsen.org/papers/rp-heaps-journal.pdf. 
  17. ↑ Brodal, Gerth Stølting; Lagogiannis, George; Tarjan, Robert E. (2012). "Strict Fibonacci heaps". Proceedings of the 44th symposium on Theory of Computing - STOC '12. pp. 1177–1184. doi:10.1145/2213977.2214082. ISBN 978-1-4503-1245-5. http://www.cs.au.dk/~gerth/papers/stoc12.pdf. 
  18. ↑ Takaoka, Tadao (1999), Theory of 2–3 Heaps, pp. 12, https://ir.canterbury.ac.nz/bitstream/handle/10092/14769/2-3heaps.pdf 
  19. ↑ Frederickson, Greg N. (1993), "An Optimal Algorithm for Selection in a Min-Heap", Information and Computation, 104, Academic Press, pp. 197–214, doi:10.1006/inco.1993.1030, http://ftp.cs.purdue.edu/research/technical_reports/1991/TR%2091-027.pdf, retrieved 2010-10-31 

External links

  • Heap at Wolfram MathWorld
  • Explanation of how the basic heap algorithms work
  • Bentley, Jon Louis (2000). Programming Pearls (2nd ed.). Addison Wesley. pp. 147–162. ISBN 0201657880. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Heap_(data_structure)&oldid=3375395"