Z-channel (information theory)

The Z-channel sees each 0 bit of a message transmitted correctly always and each 1 bit transmitted correctly with probability 1–p, due to noise across the transmission medium.

In coding theory and information theory, a Z-channel or binary asymmetric channel is a communications channel used to model the behaviour of some data storage systems.

Definition

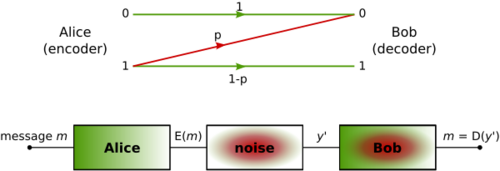
A Z-channel is a channel with binary input and binary output, where each 0 bit is transmitted correctly, but each 1 bit has probability p of being transmitted incorrectly as a 0, and probability 1–p of being transmitted correctly as a 1. In other words, if X and Y are the random variables describing the probability distributions of the input and the output of the channel, respectively, then the crossovers of the channel are characterized by the conditional probabilities:

[math]\displaystyle{ \begin{align} \operatorname {Pr} [ Y = 0 | X = 0 ] &= 1 \\ \operatorname {Pr} [ Y = 0 | X = 1 ] &= p \\ \operatorname {Pr} [ Y = 1 | X = 0 ] &= 0 \\ \operatorname {Pr} [ Y = 1 | X = 1 ] &= 1 - p \end{align} }[/math]

Capacity

The channel capacity [math]\displaystyle{ \mathsf{cap}(\mathbb{Z}) }[/math] of the Z-channel [math]\displaystyle{ \mathbb{Z} }[/math] with the crossover 1 → 0 probability p, when the input random variable X is distributed according to the Bernoulli distribution with probability [math]\displaystyle{ \alpha }[/math] for the occurrence of 0, is given by the following equation:

[math]\displaystyle{ \mathsf{cap}(\mathbb{Z}) = \mathsf{H}\left(\frac{1}{1+2^{\mathsf{s}(p)}}\right) - \frac{\mathsf{s}(p)}{1+2^{\mathsf{s}(p)}} = \log_2(1{+}2^{-\mathsf{s}(p)}) = \log_2\left(1+(1-p) p^{p/(1-p)}\right) }[/math]

where [math]\displaystyle{ \mathsf{s}(p) = \frac{\mathsf{H}(p)}{1-p} }[/math] for the binary entropy function [math]\displaystyle{ \mathsf{H}(\cdot) }[/math].

This capacity is obtained when the input variable X has Bernoulli distribution with probability [math]\displaystyle{ \alpha }[/math] of having value 0 and [math]\displaystyle{ 1-\alpha }[/math] of value 1, where:

[math]\displaystyle{ \alpha = 1 - \frac{1}{(1-p)(1+2^{\mathsf{H}(p)/(1-p)})}, }[/math]

For small p, the capacity is approximated by

[math]\displaystyle{ \mathsf{cap}(\mathbb{Z}) \approx 1- 0.5 \mathsf{H}(p) }[/math]

as compared to the capacity [math]\displaystyle{ 1{-}\mathsf{H}(p) }[/math] of the binary symmetric channel with crossover probability p.

Calculation

[math]\displaystyle{ \mathsf{cap}(\mathbb{Z}) = \max_\alpha\{\mathsf{H}(Y) - \mathsf{H}(Y \mid X)\} = \max_\alpha\Bigl\{\mathsf{H}(Y) - \sum_{x \in \{0,1\}}\mathsf{H}(Y \mid X = x) \mathsf{Prob}\{X = x\}\Bigr\} }[/math] [math]\displaystyle{ =\max_\alpha\{\mathsf{H}((1-\alpha)(1-p)) - \mathsf{H}(Y \mid X = 1) \mathsf{Prob}\{X = 1\} \} }[/math] [math]\displaystyle{ =\max_\alpha\{\mathsf{H}((1-\alpha)(1-p)) - (1-\alpha)\mathsf{H}(p) \}, }[/math] To find the maximum we differentiate [math]\displaystyle{ \frac{d}{d\alpha}\mathsf{cap}(\mathbb{Z}) = -(1-p)\log_2\left(\frac{1-(1-\alpha)(1-p)}{(1-\alpha)(1-p)}\right)+\mathsf{H}(p) }[/math] And we see the maximum is attained for [math]\displaystyle{ \alpha = 1 - \frac{1}{(1-p)(1+2^{\mathsf{H}(p)/(1-p)})}, }[/math] yielding the following value of [math]\displaystyle{ \mathsf{cap}(\mathbb{Z}) }[/math] as a function of p [math]\displaystyle{ \mathsf{cap}(\mathbb{Z}) = \mathsf{H}\left(\frac{1}{1+2^{\mathsf{s}(p)}}\right) - \frac{\mathsf{s}(p)}{1+2^{\mathsf{s}(p)}} = \log_2(1{+}2^{-\mathsf{s}(p)}) = \log_2\left(1+(1-p) p^{p/(1-p)}\right) \; \textrm{ where } \; \mathsf{s}(p) = \frac{\mathsf{H}(p)}{1-p}. }[/math]

For any p, [math]\displaystyle{ \alpha\lt 0.5 }[/math] (i.e. more 0s should be transmitted than 1s) because transmitting a 1 introduces noise. As [math]\displaystyle{ p\rightarrow 1 }[/math], the limiting value of [math]\displaystyle{ \alpha }[/math] is [math]\displaystyle{ \frac{1}{e} }[/math].

Bounds on the size of an asymmetric-error-correcting code

Define the following distance function [math]\displaystyle{ \mathsf{d}_A(\mathbf{x}, \mathbf{y}) }[/math] on the words [math]\displaystyle{ \mathbf{x}, \mathbf{y} \in \{0,1\}^n }[/math] of length n transmitted via a Z-channel

[math]\displaystyle{ \mathsf{d}_A(\mathbf{x}, \mathbf{y}) \stackrel{\vartriangle}{=} \max\left\{ \big|\{i \mid x_i = 0, y_i = 1\}\big| , \big|\{i \mid x_i = 1, y_i = 0\}\big| \right\}. }[/math]

Define the sphere [math]\displaystyle{ V_t(\mathbf{x}) }[/math] of radius t around a word [math]\displaystyle{ \mathbf{x} \in \{0,1\}^n }[/math] of length n as the set of all the words at distance t or less from [math]\displaystyle{ \mathbf{x} }[/math], in other words,

[math]\displaystyle{ V_t(\mathbf{x}) = \{\mathbf{y} \in \{0, 1\}^n \mid \mathsf{d}_A(\mathbf{x}, \mathbf{y}) \leq t\}. }[/math]

A code [math]\displaystyle{ \mathcal{C} }[/math] of length n is said to be t-asymmetric-error-correcting if for any two codewords [math]\displaystyle{ \mathbf{c}\ne \mathbf{c}' \in \{0,1\}^n }[/math], one has [math]\displaystyle{ V_t(\mathbf{c}) \cap V_t(\mathbf{c}') = \emptyset }[/math]. Denote by [math]\displaystyle{ M(n,t) }[/math] the maximum number of codewords in a t-asymmetric-error-correcting code of length n.

The Varshamov bound. For n≥1 and t≥1,

[math]\displaystyle{ M(n,t) \leq \frac{2^{n+1}}{\sum_{j = 0}^t{\left( \binom{\lfloor n/2\rfloor}{j}+\binom{\lceil n/2\rceil}{j}\right)}}. }[/math]

The constant-weight code bound. For n > 2t ≥ 2, let the sequence B₀, B₁, ..., B_n-2t-1 be defined as

[math]\displaystyle{ B_0 = 2, \quad B_i = \min_{0 \leq j \lt i}\{ B_j + A(n{+}t{+}i{-}j{-}1, 2t{+}2, t{+}i)\} }[/math] for [math]\displaystyle{ i \gt 0 }[/math].

Then [math]\displaystyle{ M(n,t) \leq B_{n-2t-1}. }[/math]

References

• MacKay, David J.C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge University Press. ISBN 0-521-64298-1. http://www.inference.phy.cam.ac.uk/mackay/itila/book.html. 
• Kløve, T. (1981). "Error correcting codes for the asymmetric channel". Technical Report 18–09–07–81 (Norway: Department of Informatics, University of Bergen). 
• Verdú, S. (1997). "Channel Capacity (73.5)". The electrical engineering handbook (second ed.). IEEE Press and CRC Press. pp. 1671-1678. 
• Tallini, L.G.; Al-Bassam, S.; Bose, B. (2002). "On the capacity and codes for the Z-channel". Proceedings of the IEEE International Symposium on Information Theory. Lausanne, Switzerland. p. 422.