Bernoulli distribution

Short description: Probability distribution modeling a coin toss which need not be fair

Bernoulli distribution

Probability mass function 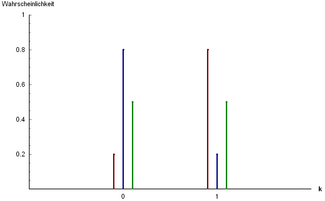Three examples of Bernoulli distribution:   $P(x=0)=0.2$ and $P(x=1)=0.8$   $P(x=0)=0.8$ and $P(x=1)=0.2$   $P(x=0)=0.5$ and $P(x=1)=0.5$
Parameters	$0\le p\le 1$ $q=1-p$
Support	$k\in \{0,1\}$
pmf	$\{\begin{array}{ll}q=1-p& \text{if }k=0\\ p& \text{if }k=1\end{array}$
CDF	$\{\begin{array}{ll}0& \text{if }k<0\\ 1-p& \text{if }0\le k<1\\ 1& \text{if }k\ge 1\end{array}$
Mean	$p$
Median	$\{\begin{array}{ll}0& \text{if }p<1/2\\ [0,1]& \text{if }p=1/2\\ 1& \text{if }p>1/2\end{array}$
Mode	$\{\begin{array}{ll}0& \text{if }p<1/2\\ 0,1& \text{if }p=1/2\\ 1& \text{if }p>1/2\end{array}$
Variance	$p(1-p)=pq$
Skewness	$\frac{q-p}{\sqrt{pq}}$
Kurtosis	$\frac{1-6pq}{pq}$
Entropy	$-q\ln q-p\ln p$
MGF	$q+p{e}^t$
CF	$q+p{e}^{it}$
PGF	$q+pz$
Fisher information	$\frac{1}{pq}$

In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability $p$ and the value 0 with probability $q=1-p$. Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcomes that are Boolean-valued: a single bit whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails", respectively, and p would be the probability of the coin landing on heads (or vice versa where 1 would represent tails and p would be the probability of tails). In particular, unfair coins would have $p\ne 1/2.$

The Bernoulli distribution is a special case of the binomial distribution where a single trial is conducted (so n would be 1 for such a binomial distribution). It is also a special case of the two-point distribution, for which the possible outcomes need not be 0 and 1.

Properties

If $X$ is a random variable with a Bernoulli distribution, then:

$$\begin{array}{rl}\mathrm{Pr}(X=1)& =p,\\ \mathrm{Pr}(X=0)& =q=1-p.\end{array}$$

The probability mass function $f$ of this distribution, over possible outcomes k, is

$$f(k;p)=\{\begin{array}{ll}p& \text{if }k=1,\\ q=1-p& \text{if }k=0.\end{array}$$

This can also be expressed as

$$f(k;p)=p^k(1-p{)}^{1-k}\text{for }k\in \{0,1\}$$

or as

$$f(k;p)=pk+(1-p)(1-k)\text{for }k\in \{0,1\}.$$

The Bernoulli distribution is a special case of the binomial distribution with $n=1.$

The kurtosis goes to infinity for high and low values of $p,$ but for $p=1/2$ the two-point distributions including the Bernoulli distribution have a lower excess kurtosis, namely −2, than any other probability distribution.

The Bernoulli distributions for $0\le p\le 1$ form an exponential family.

The maximum likelihood estimator of $p$ based on a random sample is the sample mean.

The probability mass distribution function of a Bernoulli experiment along with its corresponding cumulative distribution function

Mean

The expected value of a Bernoulli random variable $X$ is

$$\mathrm{E}[X]=p$$

This is because for a Bernoulli distributed random variable $X$ with $\mathrm{Pr}(X=1)=p$ and $\mathrm{Pr}(X=0)=q$ we find

$$\begin{array}{rl}\mathrm{E}[X]& =\mathrm{Pr}(X=1)\cdot 1+\mathrm{Pr}(X=0)\cdot 0\\ & =p\cdot 1+q\cdot 0\\ & =p.\end{array}$$

Variance

The variance of a Bernoulli distributed $X$ is

$$\mathrm{Var}[X]=pq=p(1-p)$$

We first find

$$\begin{array}{rl}\mathrm{E}[X^2]& =\mathrm{Pr}(X=1)\cdot 1^2+\mathrm{Pr}(X=0)\cdot 0^2\\ & =p\cdot 1^2+q\cdot 0^2\\ & =p=\mathrm{E}[X]\end{array}$$

From this follows

$$\begin{array}{rl}\mathrm{Var}[X]& =\mathrm{E}[X^2]-\mathrm{E}[X{]}^2=\mathrm{E}[X]-\mathrm{E}[X{]}^2\\ & =p-p^2=p(1-p)=pq\end{array}$$

With this result it is easy to prove that, for any Bernoulli distribution, its variance will have a value inside $[0,1/4]$.

Skewness

The skewness is $\frac{q-p}{\sqrt{pq}}=\frac{1-2p}{\sqrt{pq}}$. When we take the standardized Bernoulli distributed random variable $\frac{X-\mathrm{E}[X]}{\sqrt{\mathrm{Var}[X]}}$ we find that this random variable attains $\frac{q}{\sqrt{pq}}$ with probability $p$ and attains $-\frac{p}{\sqrt{pq}}$ with probability $q$. Thus we get

$$\begin{array}{rl}{\gamma }_1& =\mathrm{E}\left[{\left(\frac{X-\mathrm{E}[X]}{\sqrt{\mathrm{Var}[X]}}\right)}^3\right]\\ & =p\cdot {\left(\frac{q}{\sqrt{pq}}\right)}^3+q\cdot {(-\frac{p}{\sqrt{pq}})}^3\\ & =\frac{1}{{\sqrt{pq}}^3}(p{q}^3-q{p}^3)\\ & =\frac{pq}{{\sqrt{pq}}^3}(q^2-p^2)\\ & =\frac{(1-p{)}^2-p^2}{\sqrt{pq}}\\ & =\frac{1-2p}{\sqrt{pq}}=\frac{q-p}{\sqrt{pq}}.\end{array}$$

Higher moments and cumulants

The raw moments are all equal because $1^k=1$ and $0^k=0$.

$$\mathrm{E}[X^k]=\mathrm{Pr}(X=1)\cdot 1^k+\mathrm{Pr}(X=0)\cdot 0^k=p\cdot 1+q\cdot 0=p=\mathrm{E}[X].$$

The central moment of order $k$ is given by $${\mu }_k=(1-p)(-p{)}^k+p(1-p{)}^k.$$ The first six central moments are $$\begin{array}{rl}{\mu }_1& =0,\\ {\mu }_2& =p(1-p),\\ {\mu }_3& =p(1-p)(1-2p),\\ {\mu }_4& =p(1-p)(1-3p(1-p)),\\ {\mu }_5& =p(1-p)(1-2p)(1-2p(1-p)),\\ {\mu }_6& =p(1-p)(1-5p(1-p)(1-p(1-p))).\end{array}$$ The higher central moments can be expressed more compactly in terms of ${\mu }_2$ and ${\mu }_3$ $$\begin{array}{rl}{\mu }_4& ={\mu }_2(1-3{\mu }_2),\\ {\mu }_5& ={\mu }_3(1-2{\mu }_2),\\ {\mu }_6& ={\mu }_2(1-5{\mu }_2(1-{\mu }_2)).\end{array}$$ The first six cumulants are $$\begin{array}{rl}{\kappa }_1& =p,\\ {\kappa }_2& ={\mu }_2,\\ {\kappa }_3& ={\mu }_3,\\ {\kappa }_4& ={\mu }_2(1-6{\mu }_2),\\ {\kappa }_5& ={\mu }_3(1-12{\mu }_2),\\ {\kappa }_6& ={\mu }_2(1-30{\mu }_2(1-4{\mu }_2)).\end{array}$$

Entropy and Fisher's Information

Entropy

Entropy is a measure of uncertainty or randomness in a probability distribution. For a Bernoulli random variable $X$ with success probability $p$ and failure probability $q=1-p$, the entropy $H(X)$ is defined as:

$$\begin{array}{rl}H(X)& ={\mathbb{𝔼}}_p\ln \frac{1}{\mathrm{Pr}(X)}\\ & =-\mathrm{Pr}(X=0)\ln \mathrm{Pr}(X=0)-\mathrm{Pr}(X=1)\ln \mathrm{Pr}(X=1)\\ & =-(q\ln q+p\ln p).\end{array}$$

The entropy is maximized when $p=0.5$, indicating the highest level of uncertainty when both outcomes are equally likely. The entropy is zero when $p=0$ or $p=1$, where one outcome is certain.

Fisher's Information

Fisher information measures the amount of information that an observable random variable $X$ carries about an unknown parameter $p$ upon which the probability of $X$ depends. For the Bernoulli distribution, the Fisher information with respect to the parameter $p$ is given by:

$$I(p)=\frac{1}{pq}$$

Proof:

• The Likelihood Function for a Bernoulli random variable$X$ is: $$L(p;X)=p^X(1-p{)}^{1-X}$$ This represents the probability of observing $X$ given the parameter $p$.
• The Log-Likelihood Function is: $$\ln L(p;X)=X\ln p+(1-X)\ln (1-p)$$
• The Score Function (the first derivative of the log-likelihood with respect to $p$ is: $$\frac{\partial }{\partial p}\ln L(p;X)=\frac{X}{p}-\frac{1-X}{1-p}$$
• The second derivative of the log-likelihood function is: $$\frac{{\partial }^2}{\partial p^2}\ln L(p;X)=-\frac{X}{p^2}-\frac{1-X}{(1-p{)}^2}$$
• Fisher information is calculated as the negative expected value of the second derivative of the log-likelihood:$$\begin{array}{r}I(p)=-E[\frac{{\partial }^2}{\partial p^2}\ln L(p;X)]=-(-\frac{p}{p^2}-\frac{1-p}{(1-p{)}^2})=\frac{1}{p(1-p)}=\frac{1}{pq}\end{array}$$

It is maximized when $p=0.5$, reflecting maximum uncertainty and thus maximum information about the parameter $p$.

Related distributions

• If $X_1,\dots ,X_n$ are independent, identically distributed (i.i.d.) random variables, all Bernoulli trials with success probability p, then their sum is distributed according to a binomial distribution with parameters n and p:

  $\sum _{k=1}^n{X}_k\sim \mathrm{B}(n,p)$ (binomial distribution).

The Bernoulli distribution is simply $\mathrm{B}(1,p)$, also written as $\mathrm{B}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{i}(p).$

• The categorical distribution is the generalization of the Bernoulli distribution for variables with any constant number of discrete values.
• The Beta distribution is the conjugate prior of the Bernoulli distribution.
• The geometric distribution models the number of independent and identical Bernoulli trials needed to get one success.
• If $Y\sim \mathrm{B}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{i}\left(\frac{1}{2}\right)$, then $2Y-1$ has a Rademacher distribution.

See also

• Bernoulli process, a random process consisting of a sequence of independent Bernoulli trials
• Bernoulli sampling
• Binary entropy function
• Binary decision diagram

Further reading

• Johnson, Norman L.; Kotz, Samuel; Kemp, Adrienne W. (1993). Univariate Discrete Distributions (2nd ed.). Wiley. ISBN 0-471-54897-9. 
• Peatman, John G. (1963). Introduction to Applied Statistics. New York: Harper & Row. pp. 162–171. 

External links

• Hazewinkel, Michiel, ed. (2001), "Binomial distribution", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/b016420 .
• Weisstein, Eric W.. "Bernoulli Distribution". http://mathworld.wolfram.com/BernoulliDistribution.html. 
• Interactive graphic: Univariate Distribution Relationships.