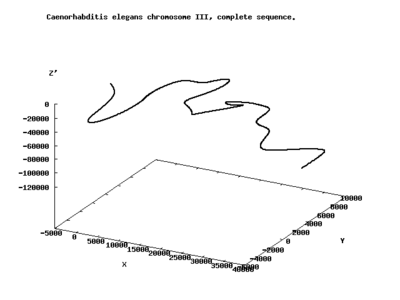
Z curve

From HandWiki
Z curve of C.elegans chromosome III

The Z curve (or Z-curve) method is a bioinformatics algorithm for genome analysis. The Z-curve is a three-dimensional curve that constitutes a unique representation of a DNA sequence, i.e., for the Z-curve and the given DNA sequence each can be uniquely reconstructed from the other.[1] The resulting curve has a zigzag shape, hence the name Z-curve.

Background

The Z Curve method was first created in 1994 as a way to visually map a DNA or RNA sequence. Different properties of the Z curve, such as its symmetry and periodicity can give unique information on the DNA sequence.[2] The Z curve is generated from a series of nodes, P0, P1,...PN, with the coordinates xn, yn, and zn (n=0,1,2...N, with N being the length of the DNA sequence). The Z curve is created by connecting each of the nodes sequentially.[3]

[math]\displaystyle{ x_{n} = (A_{n} + G_{n}) - (C_{n} + T_{n}) }[/math]

[math]\displaystyle{ y_{n} = (A_{n} + C_{n}) - (G_{n} + T_{n}) }[/math]

[math]\displaystyle{ z_{n} = (A_{n} + T_{n}) - (C_{n} + G_{n}) }[/math]

[math]\displaystyle{ n = 0, 1, 2, ... N }[/math]

Applications

Information on the distribution of nucleotides in a DNA sequence can be determined from the Z curve. The four nucleotides are combined into six different categories. The nucleotides are placed into each category by some defining characteristic and each category is designated a letter.[4]

Purine R = A, G Amino M = A, C Weak Hydrogen Bonds W = A, T
Pyrimidine Y = C, T Keto K = G, T Strong Hydrogen Bonds S = G, C

The x, y, and z components of the Z curve display the distribution of each of these categories of bases for the DNA sequence being studied. The x-component represents the distribution of purines and pyrimidine bases (R/Y). The y-component shows the distribution of amino and keto bases (M/K) and the z-component shows the distribution of strong-H bond and weak-H bond bases (S/W) in the DNA sequence.[5]

The Z-curve method has been used in many different areas of genome research, such as replication origin identification,[6][7][8][9], ab initio gene prediction,[10] isochore identification,[11] genomic island identification[12] and comparative genomics.[13] Analysis of the Z curve has also been shown to be able to predict if a gene contains introns,[14]

Research

Experiments have shown that the Z curve can be used to identify the replication origin in various organisms. One study analyzed the Z curve for multiple species of Archaea and found that the oriC is located at a sharp peak on the curve followed by a broad base. This region was rich in AT bases and had multiple repeats, which is expected for replication origin sites.[15] This and other similar studies were used to generate a program that could predict the origins of replication using the Z curve.

The Z curve has also been experimentally used to determine phylogenetic relationships. In one study, a novel coronavirus in China was analyzed using sequence analysis and the Z curve method to determine its phylogenetic relationship to other coronaviruses. It was determined that similarities and differences in related species can quickly by determined by visually examining their Z curves. An algorithm was created to identify the geometric center and other trends in the Z curve of 24 species of coronaviruses. The data was used to create a phylogenetic tree. The results matched the tree that was generated using sequence analysis. The Z curve method proved superior because while sequence analysis creates a phylogenetic tree based solely on coding sequences in the genome, the Z curve method analyzed the entire genome.[16]

References

  1. ↑ "The Z curve database: a graphic representation of genome sequences". Bioinformatics 19 (5): 593–99. 2003. doi:10.1093/bioinformatics/btg041. PMID 12651717. 
  2. ↑ Zhang, Ren; Zhang, Chun-Ting (February 1994). "Z Curves, An Intutive [sic] Tool for Visualizing and Analyzing the DNA Sequences". Journal of Biomolecular Structure and Dynamics 11 (4): 767–782. doi:10.1080/07391102.1994.10508031. PMID 8204213. 
  3. ↑ Yu, Chenglong; Deng, Mo; Zheng, Lu; He, Rong Lucy; Yang, Jie; Yau, Stephen S.-T. (2014-07-18). "DFA7, a New Method to Distinguish between Intron-Containing and Intronless Genes". PLOS ONE 9 (7): e101363. doi:10.1371/journal.pone.0101363. PMID 25036549. 
  4. ↑ Zhang, Ren; Zhang, Chun-Ting (2014-04-01). "A Brief Review: The Z-curve Theory and its Application in Genome Analysis". Current Genomics 15 (2): 78–94. doi:10.2174/1389202915999140328162433. ISSN 1389-2029. PMID 24822026. 
  5. ↑ Zhang, C. T. (1997-08-07). "A symmetrical theory of DNA sequences and its applications". Journal of Theoretical Biology 187 (3): 297–306. doi:10.1006/jtbi.1997.0401. ISSN 0022-5193. PMID 9245572. 
  6. ↑ "Identification of replication origins in archaeal genomes based on the Z-curve method". Archaea 1 (5): 335–46. 2005. doi:10.1155/2005/509646. PMID 15876567. 
  7. ↑ "Origin of replication in circular prokaryotic chromosomes". Environ. Microbiol. 8 (2): 353–61. February 2006. doi:10.1111/j.1462-2920.2005.00917.x. PMID 16423021. https://semanticscholar.org/paper/f3b6f677b5ac9c80dc7828d2a43dec8da07bb7b2. 
  8. ↑ Zhang, Ren; Zhang, Chun-Ting (2002-09-20). "Single replication origin of the archaeon Methanosarcina mazei revealed by the Z curve method". Biochemical and Biophysical Research Communications 297 (2): 396–400. doi:10.1016/s0006-291x(02)02214-3. ISSN 0006-291X. PMID 12237132. 
  9. ↑ Worning, Peder; Jensen, Lars J.; Hallin, Peter F.; Staerfeldt, Hans-Henrik; Ussery, David W. (2006-02-01). "Origin of replication in circular prokaryotic chromosomes". Environmental Microbiology 8 (2): 353–361. doi:10.1111/j.1462-2920.2005.00917.x. ISSN 1462-2912. PMID 16423021. https://semanticscholar.org/paper/f3b6f677b5ac9c80dc7828d2a43dec8da07bb7b2. 
  10. ↑ "ZCURVE: a new system for recognizing protein-coding genes in bacterial and archaeal genomes". Nucleic Acids Research 31 (6): 1780–89. 2003. doi:10.1093/nar/gkg254. PMID 12626720. 
  11. ↑ "Isochore structures in the mouse genome". Genomics 83 (3): 384–94. 2004. doi:10.1016/j.ygeno.2003.09.011. PMID 14962664. 
  12. ↑ "A systematic method to identify genomic islands and its applications in analyzing the genomes of Corynebacterium glutamicum and Vibrio vulnificus CMCP6 chromosome I". Bioinformatics 20 (5): 612–22. 2004. doi:10.1093/bioinformatics/btg453. PMID 15033867. 
  13. ↑ "Identification of genomic islands in the genome of Bacillus cereus by comparative analysis with Bacillus anthracis". Physiological Genomics 16 (1): 19–23. 2003. doi:10.1152/physiolgenomics.00170.2003. PMID 14600214. 
  14. ↑ Zhang, C. T.; Lin, Z. S.; Yan, M.; Zhang, R. (1998-06-21). "A novel approach to distinguish between intron-containing and intronless genes based on the format of Z curves". Journal of Theoretical Biology 192 (4): 467–473. doi:10.1006/jtbi.1998.0671. ISSN 0022-5193. PMID 9680720. 
  15. ↑ Zhang, Ren; Zhang, Chun-Ting (2002-09-20). "Single replication origin of the archaeon Methanosarcina mazei revealed by the Z curve method". Biochemical and Biophysical Research Communications 297 (2): 396–400. doi:10.1016/s0006-291x(02)02214-3. ISSN 0006-291X. PMID 12237132. 
  16. ↑ Zheng, Wen-Xin; Chen, Ling-Ling; Ou, Hong-Yu; Gao, Feng; Zhang, Chun-Ting (2005-08-01). "Coronavirus phylogeny based on a geometric approach". Molecular Phylogenetics and Evolution 36 (2): 224–232. doi:10.1016/j.ympev.2005.03.030. ISSN 1055-7903. PMID 15890535. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Z_curve&oldid=84879"