Zenith
Error: no inner hatnotes detected (help).
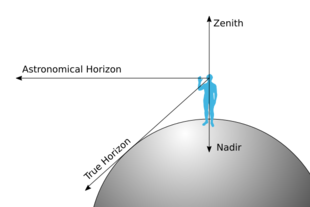
The zenith (UK: /ˈzɛnɪθ/, US: /ˈziːnɪθ/)[1] is an imaginary point directly "above" a particular location, on the celestial sphere. "Above" means in the vertical direction (plumb line) opposite to the gravity direction at that location (nadir). The zenith is the "highest" point on the celestial sphere.
Origin
The word zenith derives from an inaccurate reading of the Arabic expression سمت الرأس (Script error: The function "transl" does not exist.), meaning "direction of the head" or "path above the head", by Medieval Latin scribes in the Middle Ages (during the 14th century), possibly through Old Spanish.[2] It was reduced to samt ("direction") and miswritten as senit/cenit, the m being misread as ni. Through the Old French cenith, zenith first appeared in the 17th century.[3]
Relevance and use

The term zenith sometimes means the highest point, way, or level reached by a celestial body on its daily apparent path around a given point of observation.[4] This sense of the word is often used to describe the position of the Sun ("The sun reached its zenith..."), but to an astronomer, the Sun does not have its own zenith and is at the zenith only if it is directly overhead.
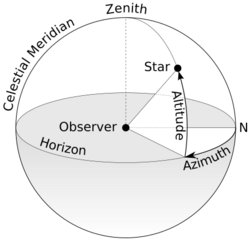
In a scientific context, the zenith is the direction of reference for measuring the zenith angle (or zenith angular distance), the angle between a direction of interest (e.g. a star) and the local zenith - that is, the complement of the altitude angle (or elevation angle).
The Sun reaches the observer's zenith when it is 90° above the horizon, and this only happens between the Tropic of Cancer and the Tropic of Capricorn. In Islamic astronomy, the passing of the Sun over the zenith of Mecca becomes the basis of the qibla observation by shadows twice a year on 27/28 May and 15/16 July.[5][6]
At a given location during the course of a day, the Sun reaches not only its zenith but also its nadir, at the antipode of that location 12 hours from solar noon.
In astronomy, the altitude in the horizontal coordinate system and the zenith angle are complementary angles, with the horizon perpendicular to the zenith. The astronomical meridian is also determined by the zenith, and is defined as a circle on the celestial sphere that passes through the zenith, nadir, and the celestial poles.
A zenith telescope is a type of telescope designed to point straight up at or near the zenith, and used for precision measurement of star positions, to simplify telescope construction, or both. The NASA Orbital Debris Observatory and the Large Zenith Telescope are both zenith telescopes, since the use of liquid mirrors meant these telescopes could only point straight up.
On the International Space Station, zenith and nadir are used instead of up and down, referring to directions within and around the station, relative to the earth.
Zenith star
Zenith stars (also "star on top", "overhead star", "latitude star")[7] are stars which culminate (pass) through the zenith. Used in celestial navigation it allowed the navigator to determine their latitudal position, since at every latitude different stars pass one's zenith, or with other words lie on the great circle of the zenith ("zenith circle"). Zenith stars are not to be confused with "steering stars"[7] of a sidereal compass rose of a sidereal compass.
See also
- Azimuth
- Geodesy
- History of geodesy
- Horizon zenith angle
- Keyhole problem
- Subsolar point
- Vertical deflection
- Horizontal coordinate system
- Analemma
References
- ↑ Jones, Daniel (2011), Cambridge English Pronouncing Dictionary (18th ed.), Cambridge University Press, ISBN 978-0-521-15255-6
- ↑ Corominas, J. (1987). Breve diccionario etimológico de la lengua castellana (3rd ed.). Madrid. pp. 144. ISBN 978-8-42492-364-8.
- ↑ "zenith". Dictionary.com Unabridged. Random House. https://www.dictionary.com/browse/zenith.
- ↑ "Zenith". Zenith. http://www.merriam-webster.com/dictionary/zenith. Retrieved March 21, 2012.
- ↑ van Gent, Robert Harry (2017). "Determining the Sacred Direction of Islam". https://www.staff.science.uu.nl/~gent0113/islam/qibla.htm.
- ↑ Khalid, Tuqa (2016). "Sun will align directly over Kaaba, Islam's holiest shrine, on Friday". CNN. https://www.cnn.com/2016/05/26/middleeast/sun-kabaa-alignment/index.html.
- ↑ 7.0 7.1 Lewis, David (1972). "We, the navigators : the ancient art of landfinding in the Pacific". Australian National University Press. https://openresearch-repository.anu.edu.au/handle/1885/114874.
Literature
- Glickman, Todd S. (2000). Glossary of meteorology. American Meteorological Society. ISBN 978-1-878220-34-9.
- McIntosh, D. H. (1972). Meteorological Glossary (5th ed.). Chemical. ISBN 978-0-8206-0228-8.
- Picoche, Jacqueline (2002). Dictionnaire étymologique du français. Paris: Le Robert. ISBN 978-2-85036-458-7.
 |