Stereohedron
In geometry and crystallography, a stereohedron is a convex polyhedron that fills space isohedrally, meaning that the symmetries of the tiling take any copy of the stereohedron to any other copy.
Two-dimensional analogues to the stereohedra are called planigons. Higher dimensional polytopes can also be stereohedra, while they would more accurately be called stereotopes.
Plesiohedra
A subset of stereohedra are called plesiohedrons, defined as the Voronoi cells of a symmetric Delone set.
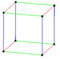
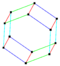
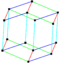
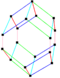
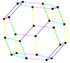
Parallelohedrons are plesiohedra which are space-filling by translation only. Edges here are colored as parallel vectors.
|
|
|
|
|
| cube | hexagonal prism | rhombic dodecahedron | elongated dodecahedron | truncated octahedron |
Other periodic stereohedra
The catoptric tessellation contain stereohedra cells. Dihedral angles are integer divisors of 180°, and are colored by their order. The first three are the fundamental domains of [math]\displaystyle{ {\tilde{C}}_3 }[/math], [math]\displaystyle{ {\tilde{B}}_3 }[/math], and [math]\displaystyle{ {\tilde{A}}_3 }[/math] symmetry, represented by Coxeter-Dynkin diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() and
and ![]()
![]()
![]() . [math]\displaystyle{ {\tilde{B}}_3 }[/math] is a half symmetry of [math]\displaystyle{ {\tilde{C}}_3 }[/math], and [math]\displaystyle{ {\tilde{A}}_3 }[/math] is a quarter symmetry.
. [math]\displaystyle{ {\tilde{B}}_3 }[/math] is a half symmetry of [math]\displaystyle{ {\tilde{C}}_3 }[/math], and [math]\displaystyle{ {\tilde{A}}_3 }[/math] is a quarter symmetry.
Any space-filling stereohedra with symmetry elements can be dissected into smaller identical cells which are also stereohedra. The name modifiers below, half, quarter, and eighth represent such dissections.
| Faces | 4 | 5 | 6 | 8 | 12 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Tetrahedra | Square pyramid | Triangular bipyramid | Cube | Octahedron | Rhombic dodecahedron | |||||||
| Images | 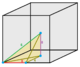 1/48 (1) |
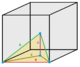 1/24 (2) |
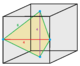 1/12 (4) |
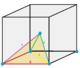 1/12 (4) |
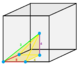 1/24 (2) |
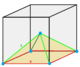 1/6 (8) |
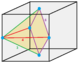 1/6 (8) |
 1/12 (4) |
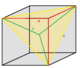 1/4 (12) |
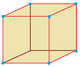 1 (48) |
 1/2 (24) |
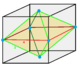 1/3 (16) |
 2 (96) |
| Symmetry (order) |
C1 1 |
C1v 2 |
D2d 4 |
C1v 2 |
C1v 2 |
C4v 8 |
C2v 4 |
C2v 4 |
C3v 6 |
Oh 48 |
D3d 12 |
D4h 16 |
Oh 48 |
| Honeycomb | Eighth pyramidille |
Triangular pyramidille |
Oblate tetrahedrille |
Half pyramidille |
Square quarter pyramidille |
Pyramidille |
Half oblate octahedrille |
Quarter oblate octahedrille |
Quarter cubille |
Cubille |
Oblate cubille |
Oblate octahedrille |
Dodecahedrille |
Other convex polyhedra that are stereohedra but not parallelohedra nor plesiohedra include the gyrobifastigium.
| Faces | 8 | 10 | 12 | |
|---|---|---|---|---|
| Symmetry (order) |
D2d (8) | D4h (16) | ||
| Images | 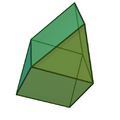
|

|

|

|
| Cell | Gyrobifastigium | Elongated gyrobifastigium |
Ten of diamonds | Elongated square bipyramid |
References
- Hazewinkel, Michiel, ed. (2001), "Stereohedron", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Stereohedron&oldid=31579
- B. N. Delone, N. N. Sandakova, Theory of stereohedra Trudy Mat. Inst. Steklov., 64 (1961) pp. 28–51 (Russian)
- Goldberg, Michael Three Infinite Families of Tetrahedral Space-Fillers Journal of Combinatorial Theory A, 16, pp. 348–354, 1974.
- Goldberg, Michael The space-filling pentahedra, Journal of Combinatorial Theory, Series A Volume 13, Issue 3, November 1972, Pages 437-443 [1] PDF
- Goldberg, Michael The Space-filling Pentahedra II, Journal of Combinatorial Theory 17 (1974), 375–378. PDF
- Goldberg, Michael On the space-filling hexahedra Geom. Dedicata, June 1977, Volume 6, Issue 1, pp 99–108 [2] PDF
- Goldberg, Michael On the space-filling heptahedra Geometriae Dedicata, June 1978, Volume 7, Issue 2, pp 175–184 [3] PDF
- Goldberg, Michael Convex Polyhedral Space-Fillers of More than Twelve Faces. Geom. Dedicata 8, 491-500, 1979.
- Goldberg, Michael On the space-filling octahedra, Geometriae Dedicata, January 1981, Volume 10, Issue 1, pp 323–335 [4] PDF
- Goldberg, Michael On the Space-filling Decahedra. Structural Topology, 1982, num. Type 10-II PDF
- Goldberg, Michael On the space-filling enneahedra Geometriae Dedicata, June 1982, Volume 12, Issue 3, pp 297–306 [5] PDF
 |

