Planigon

Short description: Convex polygon which can tile the plane by itself

Three regular polygons, eight planigons, four demiregular planigons, and six not usable planigon triangles which cannot take part in dual uniform tilings; all to scale.

In geometry, a planigon is a convex polygon that can fill the plane with only copies of itself (isotopic to the fundamental units of monohedral tessellations). In the Euclidean plane there are 3 regular planigons; equilateral triangle, squares, and regular hexagons; and 8 semiregular planigons; and 4 demiregular planigons which can tile the plane only with other planigons.

All angles of a planigon are whole divisors of 360°. Tilings are made by edge-to-edge connections by perpendicular bisectors of the edges of the original uniform lattice, or centroids along common edges (they coincide).

Tilings made from planigons can be seen as dual tilings to the regular, semiregular, and demiregular tilings of the plane by regular polygons.

History

In the 1987 book, Tilings and Patterns, Branko Grünbaum calls the vertex-uniform tilings Archimedean in parallel to the Archimedean solids. Their dual tilings are called Laves tilings in honor of crystallographer Fritz Laves. They're also called Shubnikov–Laves tilings after Shubnikov, Alekseĭ Vasilʹevich. John Conway calls the uniform duals Catalan tilings, in parallel to the Catalan solid polyhedra.

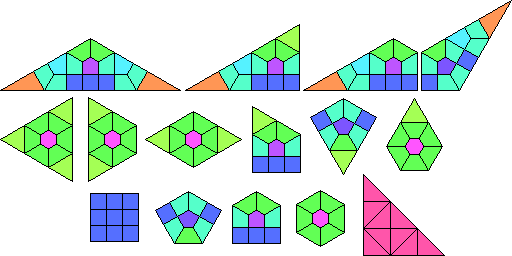
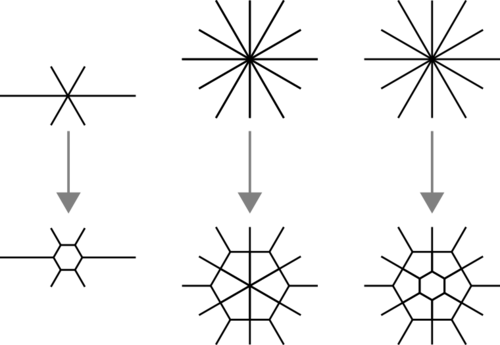
The Laves tilings have vertices at the centers of the regular polygons, and edges connecting centers of regular polygons that share an edge. The tiles of the Laves tilings are called planigons. This includes the 3 regular tiles (triangle, square and hexagon) and 8 irregular ones. Each vertex has edges evenly spaced around it. Three dimensional analogues of the planigons are called stereohedrons.

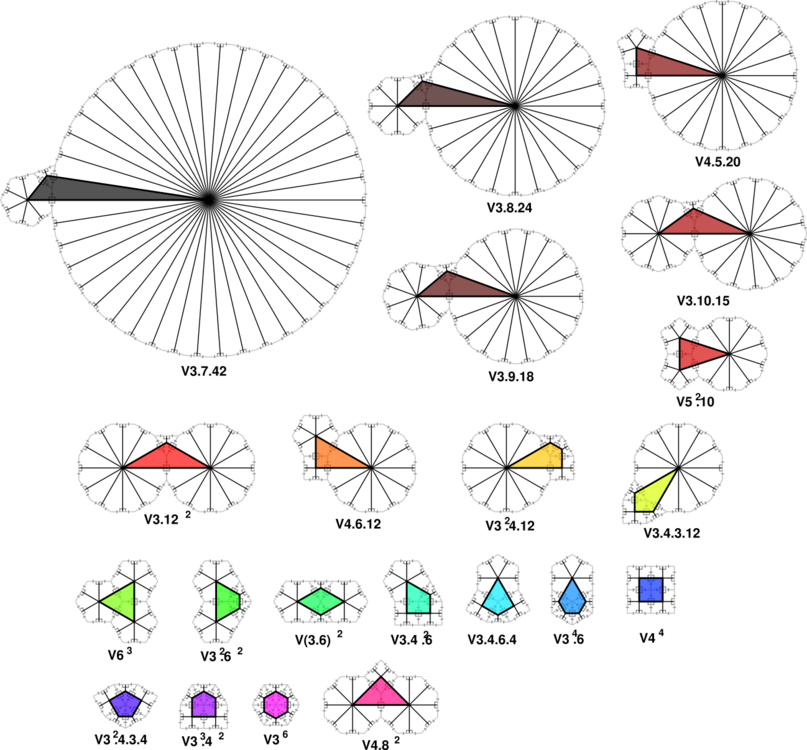
These tilings are listed by their face configuration, the number of faces at each vertex of a face. For example V4.8.8 (or V4.8²) means isosceles triangle tiles with one corner with four triangles, and two corners containing eight triangles.

Construction

The Conway operation of dual interchanges faces and vertices. In Archimedean solids and k-uniform tilings alike, the new vertex coincides with the center of each regular face, or the centroid. In the Euclidean (plane) case; in order to make new faces around each original vertex, the centroids must be connected by new edges, each of which must intersect exactly one of the original edges. Since regular polygons have dihedral symmetry, we see that these new centroid-centroid edges must be perpendicular bisectors of the common original edges (e.g. the centroid lies on all edge perpendicular bisectors of a regular polygon). Thus, the edges of k-dual uniform tilings coincide with centroid-to-edge-midpoint line segments of all regular polygons in the k-uniform tilings.

Planigon Constructions

Centroid-to-Centroid	12-5 Dodecagram

Using the 12-5 Dodecagram (Above)

All 14 uniform usable regular vertex planigons also hail from the 6-5 dodecagram (where each segment subtends [math]\displaystyle{ 5\pi/6 }[/math] radians, or 150 degrees).

The incircle of this dodecagram demonstrates that all the 14 VRPs are cocyclic, as alternatively shown by circle packings. The ratio of the incircle to the circumcircle is:

[math]\displaystyle{ \sin\frac{\pi}{12}=\sin 15^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}\approx 0.258819 }[/math]

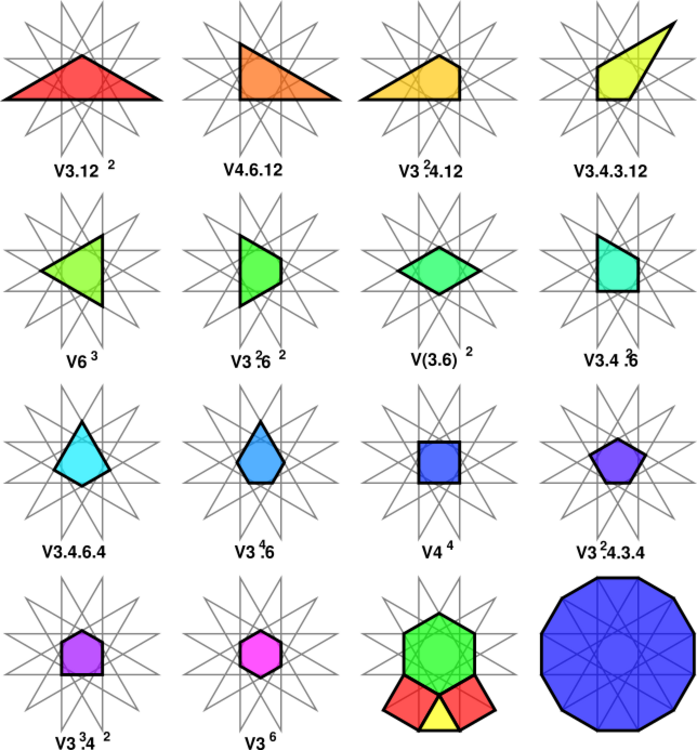
and the convex hull is precisely the regular dodecagons in the k-uniform tiling. The equilateral triangle, square, regular hexagon, and regular dodecagon; are shown above with the VRPs.

In fact, any group of planigons can be constructed from the edges of a [math]\displaystyle{ 2k\text{-}(k-1) }[/math] polygram, where [math]\displaystyle{ k=\gcd(n_1,\dots,n_m) }[/math] and [math]\displaystyle{ n_i }[/math] is the number of sides of sides in the RP adjacent to each involved vertex figure. This is because the circumradius [math]\displaystyle{ \frac{1}{2}\csc\frac{\pi}{n_i} }[/math] of any regular [math]\displaystyle{ n_i }[/math]-gon (from the vertex to the centroid) is the same as the distance from the center of the polygram to its line segments which intersect at the angle [math]\displaystyle{ 2\pi/n_i }[/math], since all [math]\displaystyle{ 2k\text{-}(k-1) }[/math] polygrams admit incircles of inradii [math]\displaystyle{ 1/2 }[/math] tangent to all its sides.

Regular Vertices

In Tilings and Patterns, Grünbaum also constructed the Laves tilings using monohedral tiles with regular vertices. A vertex is regular if all angles emanating from it are equal. In other words:

1. All vertices are regular,
2. All Laves planigons are congruent.

In this way, all Laves tilings are unique except for the square tiling (1 degree of freedom), barn pentagonal tiling (1 degree of freedom), and hexagonal tiling (2 degrees of freedom):

Tiling Variants

Square	Barn Pentagon	Hexagon

When applied to higher dual co-uniform tilings, all dual coregular planigons can be distorted except for the triangles (AAA similarity), with examples below:

Tiling Variants

S2TCH

I2RFH

IrDC

FH (p6)

sBH (short)

CB (pgg)

Edge-to-Edge Correspondence

Alternatively, k-dual uniform tilings (and all 21 planigons) can be constructed by forming new centroid-edge midpoint line segments of the original regular polygons (dissecting the regular n-gons into n congruent deltoids or ortho), and then removing the original edges (leaving the dual). Complete planigons will form around interior vertices, and line segments of (many possible) planigons will form around boundary vertices, giving a 1-to-1 edge k-dual uniform lattice. On the other hand, centroid-centroid connecting only yields interior planigons, but this construction is nonetheless equivalent to the original in the interior. If the k-uniform tiling fills the entire frame, then so will the k-dual uniform tiling, and the boundary line segments can be ignored (equivalent to original construction).

Edge-to-Edge/Interior Construction of a Dual Uniform Tiling

Orig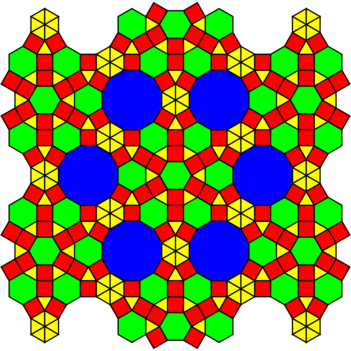
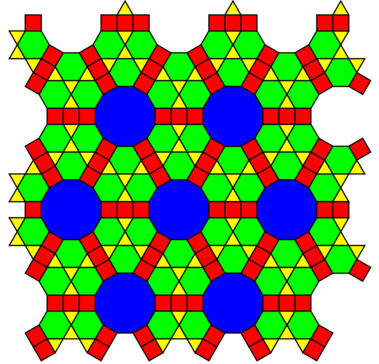
Dual
Comp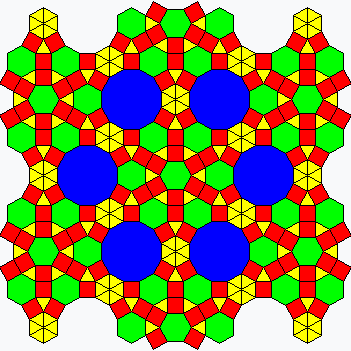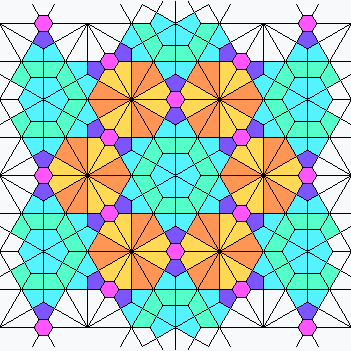

Affine Linear Expansion

Starting from the regular polygons of a k-uniform tiling, we can scale all regular polygons about their centroids over a linear factor [math]\displaystyle{ 0\lt x\lt 1 }[/math], and put planigons in the vertex-figure gaps of scale [math]\displaystyle{ 1-x }[/math]. The original tiling starts from x = 0 and ends at the dual tiling (x = 1).[1] This is true because the circumradii of the regular polygons are the same as the diagonals from the incenters of the planigons to their co-vertices, as we could see in the construction above (or by applying a kis-operator to both the uniform and dual adds the same join lattice [2]). Therefore, scaling the regular polygons by [math]\displaystyle{ x }[/math] yields proportional plangions of scale [math]\displaystyle{ 1-x }[/math] at the vertex-figure gaps. The intermediate stages are equivalent to expand (hence the expansion), and the union of all dyadic-[math]\displaystyle{ x }[/math] affine linear expansions of a tiling is closed under expansion (contains all expands).[3] An example is shown below:

Affine Linear Expansion	Comparison

Derivation of all possible planigons

For edge-to-edge Euclidean tilings, the interior angles of the convex polygons meeting at a vertex must add to 360 degrees. A regular n-gon has internal angle [math]\displaystyle{ \left(1-\frac{2}{n}\right)180^\circ }[/math] degrees. There are seventeen combinations of regular polygons whose internal angles add up to 360 degrees, each being referred to as a species of vertex; in four cases there are two distinct cyclic orders of the polygons, yielding twenty-one types of vertex.

In fact, with the vertex (interior) angles [math]\displaystyle{ 60^\circ,90^\circ,108^\circ,120^\circ,128\frac{4}{7}^\circ,135^\circ,140^\circ,144^\circ, 147\frac{3}{11}^\circ,150^\circ,\dots }[/math], we can find all combinations of admissible corner angles according to the following rules:

1. Every vertex has at least degree 3 (a degree-2 vertex must have two straight angles or one reflex angle);
2. If the vertex has degree [math]\displaystyle{ d }[/math], the smallest [math]\displaystyle{ d-1 }[/math] polygon vertex angles sum to over [math]\displaystyle{ 180^{\circ} }[/math];
3. The vertex angles add to [math]\displaystyle{ 360^{\circ} }[/math], and must be angles of regular polygons of positive integer sides (of the sequence [math]\displaystyle{ 60^\circ,90^\circ,108^\circ,120^\circ,128\frac{4}{7}^\circ,135^\circ,140^\circ,144^\circ, 147\frac{3}{11}^\circ,150^\circ,\dots }[/math]).

Using the rules generates the list below:

Clusters of planigons which cannot tile the plane. Note the 8-cluster of V3.8.24 and the 10-cluster of V3.10.15 imply overlaps for the 24-gons and 15-gons, respectively. Also, V4.5.20 and V5².10 can generate lines and curves, but those cannot be completed without overlap.

Arrangements of regular polygons around a vertex

Degree-6 vertex	Degree-5 vertex	Degree-4 vertex	Degree-3 vertex
[math]\displaystyle{ 60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}~(\times 1) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}\text{-}90^{\circ}\text{-}90^{\circ}~(\times 2) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}60^{\circ}\text{-}90^{\circ}\text{-}150^{\circ}~(\times 2) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}128\frac{4}{7}^{\circ}\text{-}171\frac{3}{7}^{\circ}~(\times 1) }[/math]
	[math]\displaystyle{ 60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}\text{-}60^{\circ}\text{-}120^{\circ}~(\times 1) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}60^{\circ}\text{-}120^{\circ}\text{-}120^{\circ}~(\times 2) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}135^{\circ}\text{-}165^{\circ}~(\times 1) }[/math]
		[math]\displaystyle{ 60^{\circ}\text{-}90^{\circ}\text{-}90^{\circ}\text{-}120^{\circ}~(\times 2) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}140^{\circ}\text{-}160^{\circ}~(\times 1) }[/math]
		[math]\displaystyle{ 90^{\circ}\text{-}90^{\circ}\text{-}90^{\circ}\text{-}90^{\circ}~(\times 1) }[/math]	[math]\displaystyle{ 60^{\circ}\text{-}144^{\circ}\text{-}156~(\times 1) }[/math]
			[math]\displaystyle{ 60^{\circ}\text{-}150^{\circ}\text{-}150^{\circ}~(\times 1) }[/math]
			[math]\displaystyle{ 90^{\circ}\text{-}108^{\circ}\text{-}162^{\circ}~(\times 1) }[/math]
			[math]\displaystyle{ 90^{\circ}\text{-}120^{\circ}\text{-}150^{\circ}~(\times 1) }[/math]
			[math]\displaystyle{ 90^{\circ}\text{-}135^{\circ}\text{-}135^{\circ}~(\times 1) }[/math]*
			[math]\displaystyle{ 108^{\circ}\text{-}108^{\circ}\text{-}144^{\circ}~(\times 1) }[/math]
			[math]\displaystyle{ 120^{\circ}\text{-}120^{\circ}\text{-}120^{\circ}~(\times 1) }[/math]

*The [math]\displaystyle{ 90^{\circ}\text{-}135^{\circ}\text{-}135^{\circ}~(\times 1) }[/math] cannot coexist with any other vertex types.

The solution to Challenge Problem 9.46, Geometry (Rusczyk), is in the Degree 3 Vertex column above. A triangle with a hendecagon (11-gon) yields a 13.2-gon, a square with a heptagon (7-gon) yields a 9.3333-gon, and a pentagon with a hexagon yields a 7.5-gon). Hence there are [math]\displaystyle{ 1(1)+(1(2)+1)+(3(2)+1)+10=21 }[/math] combinations of regular polygons which meet at a vertex.

Plangions in the plane

Only eleven of these angle combinations can occur in a Laves Tiling of planigons.

In particular, if three polygons meet at a vertex and one has an odd number of sides, the other two polygons must be the same. If they are not, they would have to alternate around the first polygon, which is impossible if its number of sides is odd. By that restriction these six cannot appear in any tiling of regular polygons:

Six planigons which cannot tile the plane.

On the other hand, these four can be used in k-dual-uniform tilings:

There is one demiregular dual for each planigon V3².4.12, V3.4.3.12, V3².6², V3.4².6. And all quadrilaterals can tile the plane.

Finally, assuming unit side length, all regular polygons and usable planigons have side-lengths and areas as shown below in the table:

Regular Polygons and Planigons

Regular Polygons		Planigons
Triangle	Area: [math]\displaystyle{ \frac{\sqrt{3}}{4} }[/math] Side Lengths: 1	V3.122 (O)	Area: [math]\displaystyle{ 1+\frac{7}{4\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ 2+\sqrt{3},1+\frac{2}{\sqrt{3}} }[/math]	V32.62 (I)	Area: [math]\displaystyle{ \frac{2}{\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ \sqrt{3},\frac{2}{\sqrt{3}},\frac{1}{\sqrt{3}} }[/math]	V44 (s)	Area: 1 Side Lengths: 1
Square	Area: 1 Side Lengths: 1	V4.6.12 (3)	Area: [math]\displaystyle{ \frac{3}{4}+\frac{3\sqrt{3}}{2} }[/math] Side Lengths: [math]\displaystyle{ 1+\sqrt{3},\frac{3+\sqrt{3}}{2},\frac{1+\sqrt{3}}{2} }[/math]	V(3.6)2 (R)	Area: [math]\displaystyle{ \frac{2}{\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ \frac{2}{\sqrt{3}} }[/math]	V32.4.3.4 (C)	Area: [math]\displaystyle{ \frac{1}{2}+\frac{\sqrt{3}}{4} }[/math] Side Lengths: [math]\displaystyle{ \frac{1}{2}+\frac{1}{2\sqrt{3}},\frac{1}{\sqrt{3}} }[/math]
Hexagon	Area: [math]\displaystyle{ \frac{3\sqrt{3}}{2} }[/math] Side Lengths: 1	V32.4.12 (S)	Area: [math]\displaystyle{ \frac{3}{4}+\frac{5}{4\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ \frac{3+\sqrt{3}}{2},1+\frac{2}{\sqrt{3}},\frac{1}{2}+\frac{1}{2\sqrt{3}},\frac{1}{\sqrt{3}} }[/math]	V3.42.6 (r)	Area: [math]\displaystyle{ \frac{1}{2}+\frac{1}{\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ \frac{1+\sqrt{3}}{2},\frac{2}{\sqrt{3}},1,\frac{1}{2}+\frac{1}{2\sqrt{3}} }[/math]	V33.42 (B)	Area: [math]\displaystyle{ \frac{1}{2}+\frac{\sqrt{3}}{4} }[/math] Side Lengths: [math]\displaystyle{ 1,\frac{1}{2}+\frac{1}{2\sqrt{3}},\frac{1}{\sqrt{3}} }[/math]
Octagon	Area: [math]\displaystyle{ 2+2\sqrt{2} }[/math] Side Lengths: 1	V3.4.3.12 (T)	Area: [math]\displaystyle{ \frac{3}{4}+\frac{5}{4\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ 1+\frac{2}{\sqrt{3}},\frac{1}{2}+\frac{1}{2\sqrt{3}} }[/math]	V3.4.6.4 (D)	Area: [math]\displaystyle{ \frac{1}{2}+\frac{1}{\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ \frac{1+\sqrt{3}}{2},\frac{1}{2}+\frac{1}{2\sqrt{3}} }[/math]	V36 (H)	Area: [math]\displaystyle{ \frac{\sqrt{3}}{2} }[/math] Side Lengths: [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math]
Dodecagon	Area: [math]\displaystyle{ 6+3\sqrt{3} }[/math] Side Lengths: 1	V63 (E)	Area: [math]\displaystyle{ \frac{3\sqrt{3}}{4} }[/math] Side Lengths: [math]\displaystyle{ \sqrt{3} }[/math]	V34.6 (F)	Area: [math]\displaystyle{ \frac{7}{4\sqrt{3}} }[/math] Side Lengths: [math]\displaystyle{ \frac{2}{\sqrt{3}},\frac{1}{\sqrt{3}} }[/math]	V4.82 (i)	Area: [math]\displaystyle{ \frac{3}{4}+\frac{1}{\sqrt{2}} }[/math] Side Lengths: [math]\displaystyle{ 1+\frac{1}{\sqrt{2}},\frac{1}{2}+\frac{1}{\sqrt{2}} }[/math]

Number of Dual Uniform Tilings

Every dual uniform tiling is in a 1:1 correspondence with the corresponding uniform tiling, by construction of the planigons above and superimposition.

k-dual-uniform, m-Catalaves tiling counts

	m-Catalaves
		1	2	3	4	5	6	Total
k-dual-uniform	1	11						11
	2	0	20					20
	3	0	22	39				61
	4	0	33	85	33			151
	5	0	74	149	94	15		332
	6	0	100	284	187	92	10	673
	Total	11	∞	∞	∞	∞	∞	∞

Such periodic tilings may be classified by the number of orbits of vertices, edges and tiles. If there are k orbits of planigons, a tiling is known as k-dual-uniform or k-isohedral; if there are t orbits of dual vertices, as t-isogonal; if there are e orbits of edges, as e-isotoxal.

k-dual-uniform tilings with the same vertex faces can be further identified by their wallpaper group symmetry, which is identical to that of the corresponding k-uniform tiling.

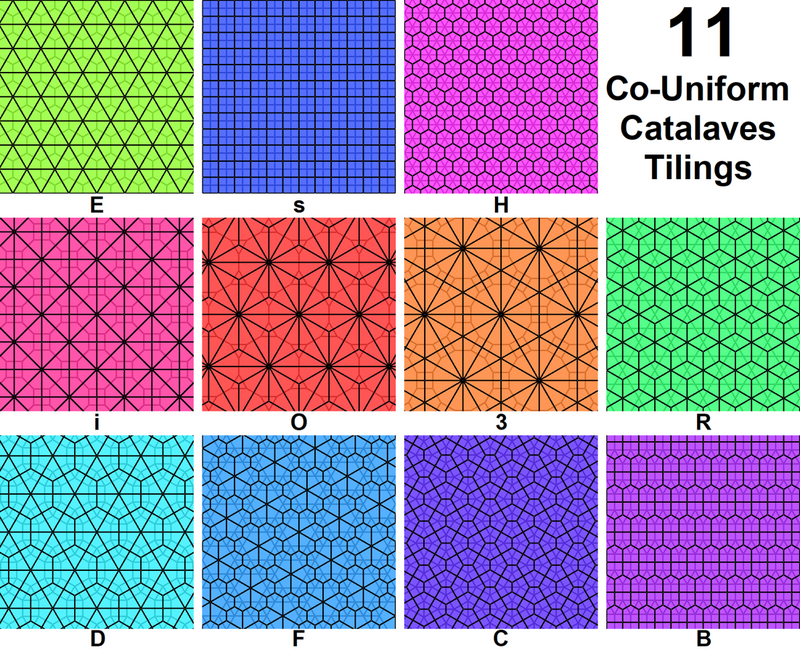
1-dual-uniform tilings include 3 regular tilings, and 8 Laves tilings, with 2 or more types of regular degree vertices. There are 20 2-dual-uniform tilings, 61 3-dual-uniform tilings, 151 4-dual-uniform tilings, 332 5-dual-uniform tilings and 673 6--dualuniform tilings. Each can be grouped by the number m of distinct vertex figures, which are also called m-Archimedean tilings.

Finally, if the number of types of planigons is the same as the uniformity (m = k below), then the tiling is said to be dual Krotenheerdt. In general, the uniformity is greater than or equal to the number of types of vertices (m ≥ k), as different types of planigons necessarily have different orbits, but not vice versa. Setting m = n = k, there are 11 such dual tilings for n = 1; 20 such dual tilings for n = 2; 39 such dual tilings for n = 3; 33 such dual tilings for n = 4; 15 such dual tilings for n = 5; 10 such dual tilings for n = 6; and 7 such dual tilings for n = 7.

Regular and Laves tilings

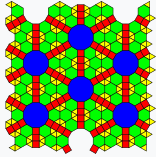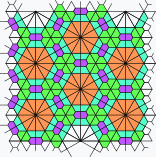
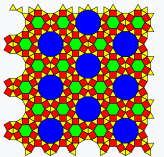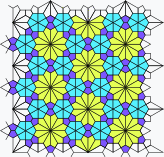
The 3 regular and 8 semiregular Laves tilings are shown, with planigons colored according to area as in the construction:

Higher Dual Uniform Tilings

Insets of Dual Planigons into Higher Degree Vertices

A manhole in Central Park with tiling CH (V3².4.3.4,V3⁶).

• A degree-six vertex can be replaced by a center regular hexagon and six edges emanating thereof;
• A degree-twelve vertex can be replaced by six deltoids (a center deltoidal hexagon) and twelve edges emanating thereof;
• A degree-twelve vertex can be replaced by six Cairo pentagons, a center hexagon, and twelve edges emanating thereof (by dissecting the degree-6 vertex in the center of the previous example).

Minor	Major	Full	Substitutions
Dual Processes (Insets)

This is done above for the dual of the 3-4-6-12 tiling. The corresponding uniform process is dissection, and is shown here.

2-Dual-Uniform

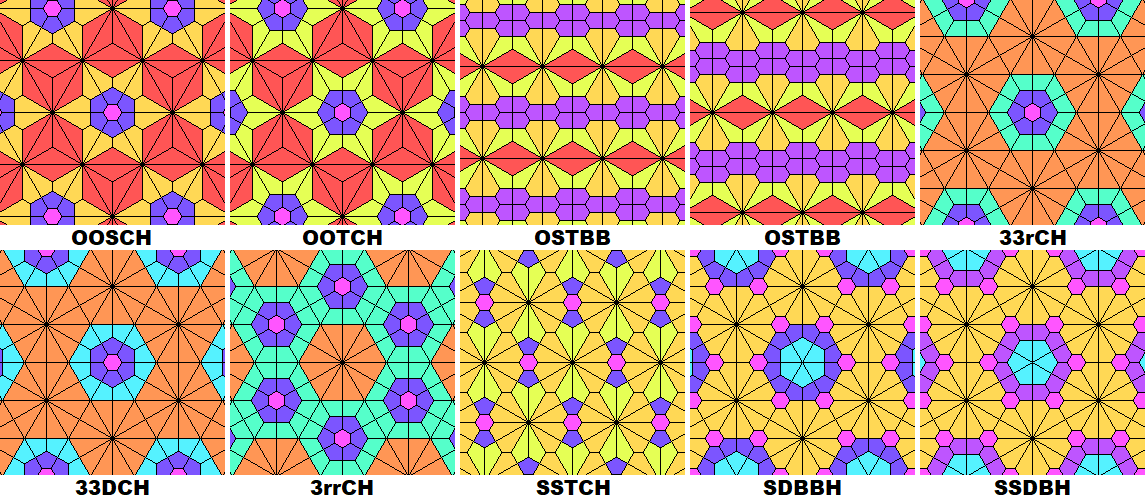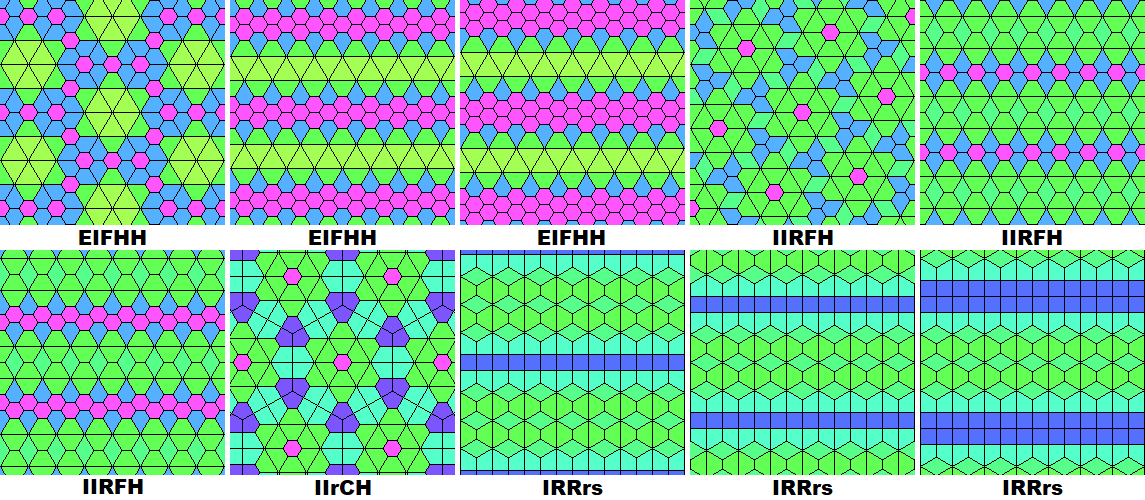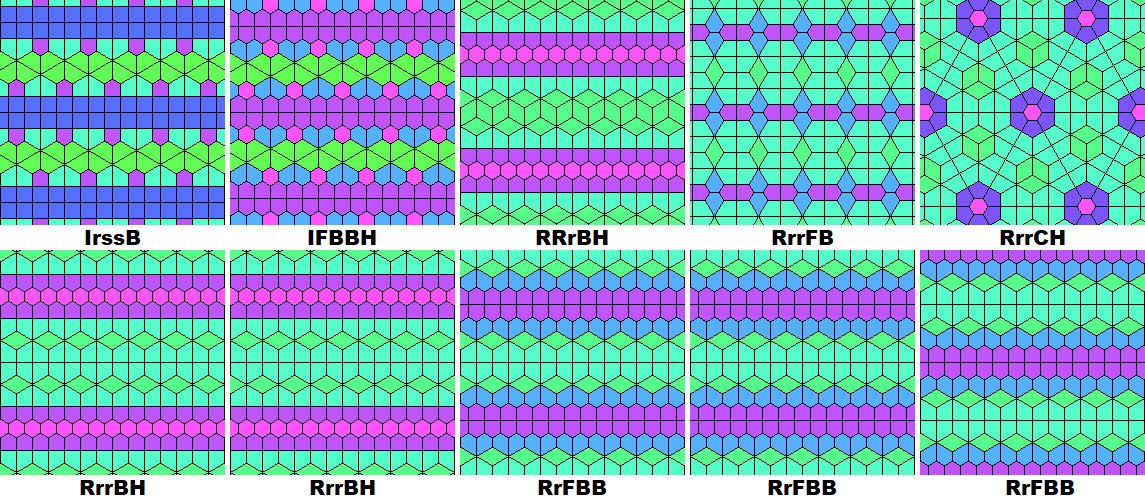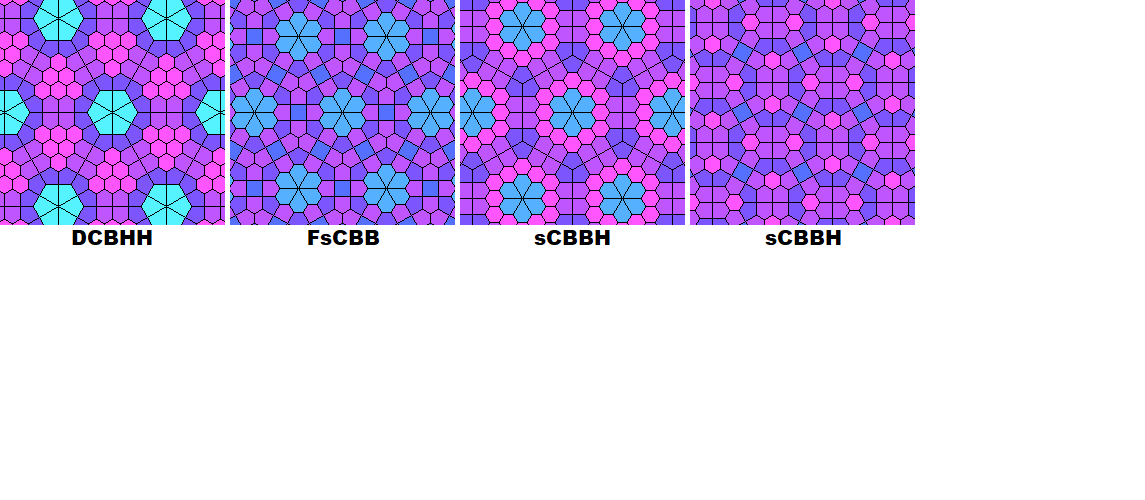
There are 20 tilings made from 2 types of planigons, the dual of 2-uniform tilings (Krotenheerdt Duals):

3-Dual-Uniform

There are 39 tilings made from 3 types of planigons (Krotenheerdt Duals):

4-Dual-Uniform

There are 33 tilings made from 4 types of planigons (Krotenheerdt Duals):

5-Dual-Uniform

There are 15 5-uniform dual tilings with 5 unique planigons:

Krotenheerdt duals with six planigons

There are 10 6-uniform dual tilings with 6 unique planigons:

Krotenheerdt duals with seven planigons

There are 7 7-uniform dual tilings with 7 unique planigons:

The last two dual uniform-7 tilings have the same vertex types, even though they look nothing alike!

From [math]\displaystyle{ n\ge 8 }[/math] onward, there are no uniform n tilings with n vertex types, or no uniform n duals with n distinct (semi)planigons.

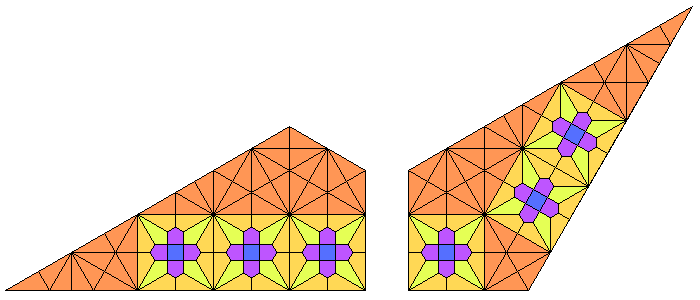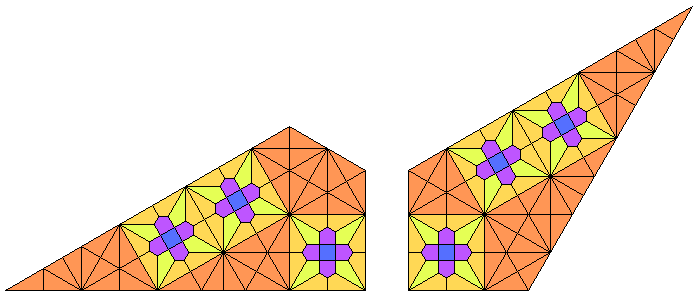
Fractalizing Dual k-Uniform Tilings

There are many ways of generating new k-dual-uniform tilings from other k-uniform tilings. Three ways is to scale by [math]\displaystyle{ 1+\sqrt{3},2+\sqrt{3},3+\sqrt{3} }[/math] as seen below:

Fractalizing Examples

	Original	Semi-Fractalization	Truncated Hexagonal Tiling	Truncated Trihexagonal Tiling
Dual Fractalizing

Large Fractalization

To enlarge the planigons V3².4.12 and V3.4.3.12 using the truncated trihexagonal method, a scale factor of [math]\displaystyle{ 2(3+\sqrt{3}) }[/math] must be applied:

Big Fractalization

By two 9-uniform tilings in a big fractalization is achieved by a scale factor of 3 in all planigons. In the case of s,C,B,H its own planigon is in the exact center:

The two 9-uniform tilings are shown below, fractalizations of the demiregulars DC and DB, and a general example on S²TC:

9-Uniform	S2TC Big Fractalization
3Ir3Ds2B (of DB) 3Ir4DsC (of DC)	S2TC Big Fractalization

Miscellaneous

Centroid-Centroid Construction

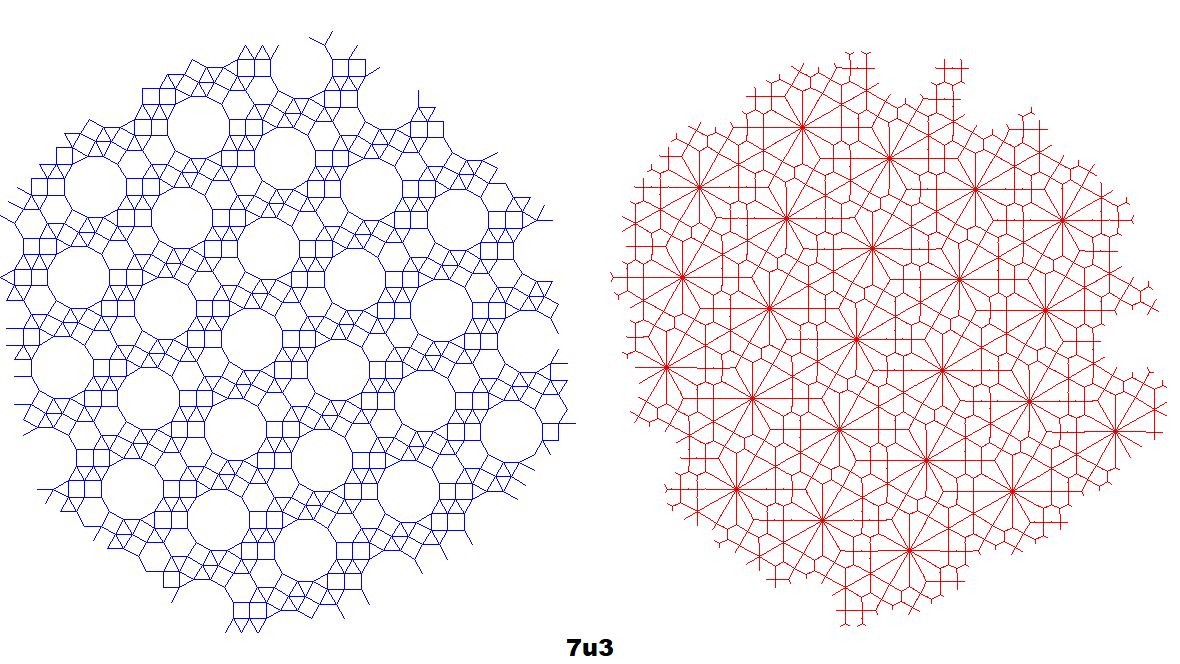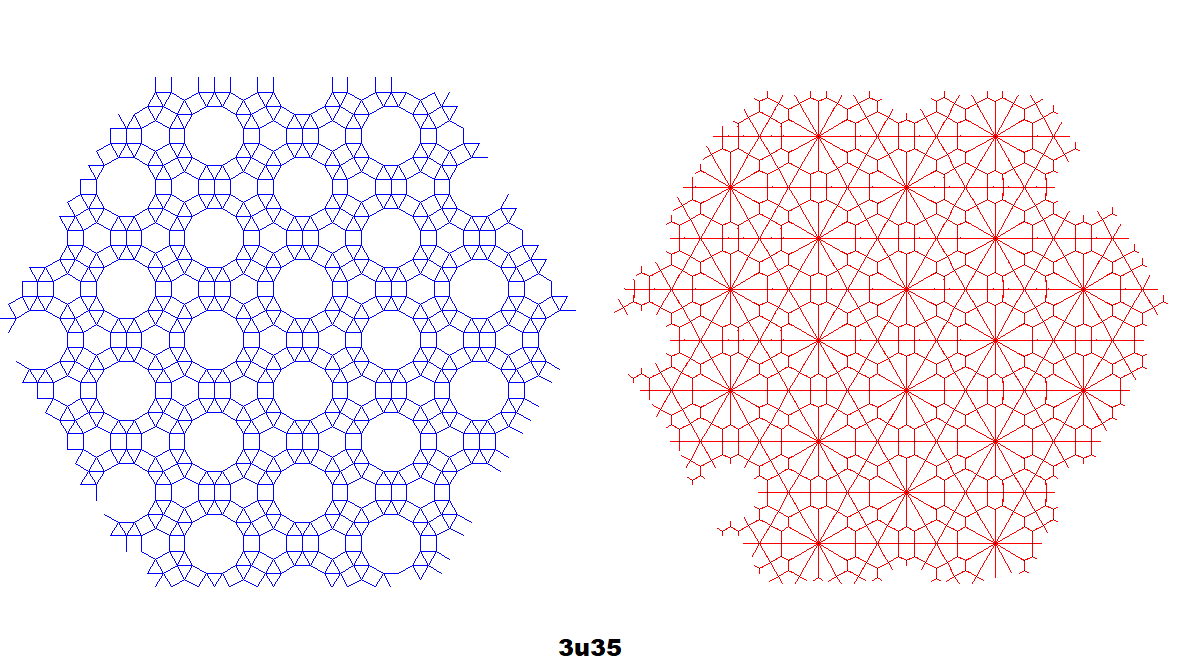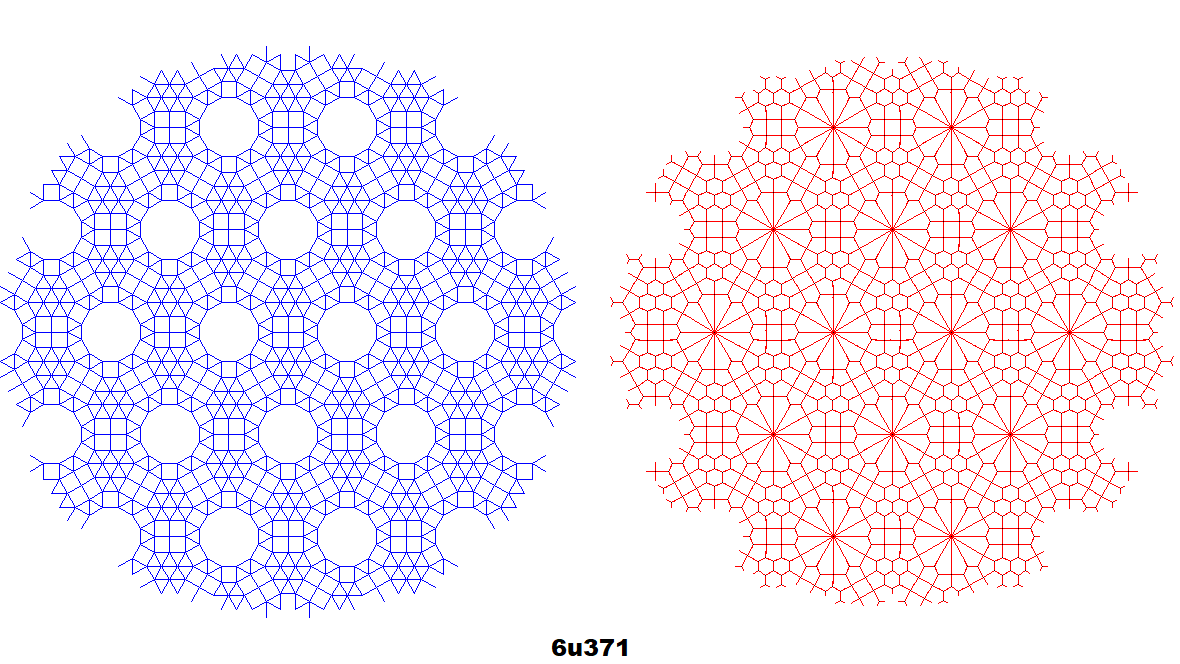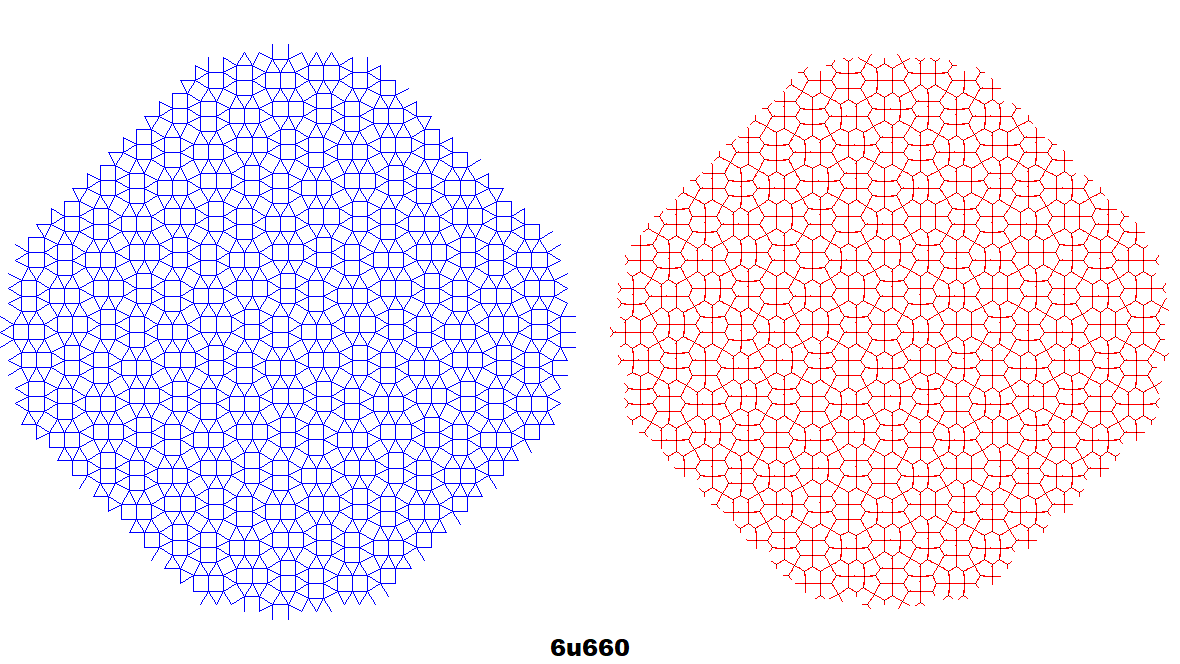
Dual co-uniform tilings (red) along with the originals (blue) of selected tilings. Generated by centroid-edge midpoint construction by polygon-centroid-vertex detection, rounding the angle of each co-edge to the nearest 15 degrees. Since the unit size of tilings varies from 15 to 18 pixels and every regular polygon slightly differs, there is some overlap or breaks of dual edges (an 18-pixel size generator incorrectly generates co-edges from five 15-pixel size tilings, classifying some squares as triangles).

Other Edge-Edge Construction Comparisons

Other edge-edge construction comparisons. Rotates every 3 seconds.

Comparisons

SDB	3IrB	TDDC	IIRF	rFBH	OOOOT	3SrFCBH	O33STIr2C2B

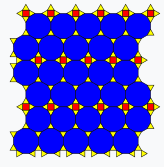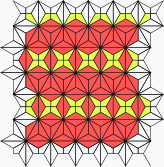
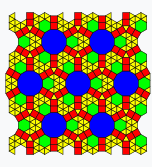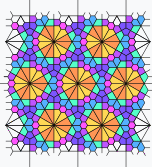
Affine Linear Expansions

Below are affine linear expansions of other uniform tilings, from the original to the dual and back:

Affine Linear Expansions

8-Uniform 3STDC	12-Uniform 3STRrD	12-Uniform O3STIrCB	13-Uniform All Slab	16-Uniform OSTEIrCB	24-Uniform All Planigons

The first 12-uniform tiling contains all planigons with three types of vertices, and the second 12-uniform tiling contains all types of edges.

Optimized Tilings

A 14-Catalaves dual uniform tiling using p4g. Such tilings can assume any wallpaper group except for p4m since p4m only admits planigons O, S, T, D, s, C, B, H.

If [math]\displaystyle{ a }[/math]-[math]\displaystyle{ b }[/math] tiling means [math]\displaystyle{ a }[/math] dual uniform, [math]\displaystyle{ b }[/math] Catalaves tiling, then there exists a 11-9 tiling, a 13-10 tiling, 15-11 tiling, a 19-12 tiling, two 22-13 tilings, and a 24-14 tiling. Also exists a 13-8 slab tiling and a 14-10 non-clock tiling. Finally, there are 7-5 tilings using all clock planigons:

11-9	13-10	15-11	19-12	22-13
OSTRrD2sC2B	3S2IRr3DFCBH	3STEIRrFCB5H	O3ST3Rr2D3FsCB3H	O32ST2EIRr4D2FCB4H O32ST2EIRr3DFC2B5H
24-14	13-8 Slab	14-10 Non Clock	7-5 All Clock
O32S3TEIRr2DFsC2B6H	EI2Rr2F2s2B2H	EIRr3DFsCB2H	O33STB	O32ST2D

Circle Packing

Each uniform tiling corresponds to a circle packing, in which circles of diameter 1 are placed at all vertex points, corresponding to the planigons. Below are the circle packings of the Optimized Tilings and all-edge tiling:

Circles are colored according to vertex type, and gaps are colored according to regular polygon.

5-dual-uniform 4-Catalaves tilings

A slideshow of all 94 5-dual-uniform tilings with 4 distinct planigons. Changes every 6 seconds, cycles every 60 seconds.

Clock Tilings

All tilings with regular dodecagons in are shown below, alternating between uniform and dual co-uniform every 5 seconds:

All tilings with regular dodecagons are shown below, alternating between uniform and dual co-uniform every 5 seconds.

65 k-Uniform Tilings

A comparison of 65 k uniform tilings in uniform planar tilings and their dual uniform tilings. The two lower rows coincide and are to scale:

A comparison of 65 k uniform tilings in uniform planar tilings and their dual uniform tilings. The two lower rows coincide and are to scale.

References

• Planigon tessellation cellular automata Alexander Korobov, 30 September 1999
• B. N. Delone, “Theory of planigons”, Izv. Akad. Nauk SSSR Ser. Mat., 23:3 (1959), 365–386