Apollonius's theorem
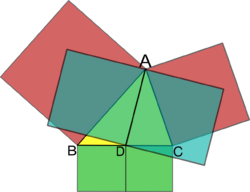
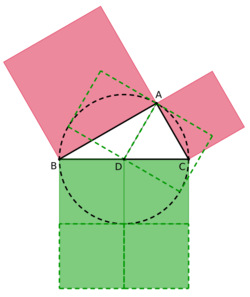
In geometry, Apollonius's theorem is a theorem relating the length of a median of a triangle to the lengths of its sides. It states that "the sum of the squares of any two sides of any triangle equals twice the square on half the third side, together with twice the square on the median bisecting the third side".
Specifically, in any triangle [math]\displaystyle{ ABC, }[/math] if [math]\displaystyle{ AD }[/math] is a median, then [math]\displaystyle{ 2(|AB|^2+|AC|^2)=|BC|^2+4|AD|^2. }[/math] It is a special case of Stewart's theorem. For an isosceles triangle with [math]\displaystyle{ |AB| = |AC|, }[/math] the median [math]\displaystyle{ AD }[/math] is perpendicular to [math]\displaystyle{ BC }[/math] and the theorem reduces to the Pythagorean theorem for triangle [math]\displaystyle{ ADB }[/math] (or triangle [math]\displaystyle{ ADC }[/math]). From the fact that the diagonals of a parallelogram bisect each other, the theorem is equivalent to the parallelogram law.
The theorem is named for the ancient Greek mathematician Apollonius of Perga.
Proof
The theorem can be proved as a special case of Stewart's theorem, or can be proved using vectors (see parallelogram law). The following is an independent proof using the law of cosines.[1]
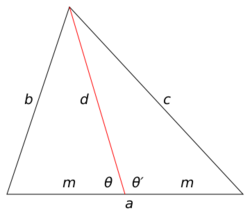
Let the triangle have sides [math]\displaystyle{ a, b, c }[/math] with a median [math]\displaystyle{ d }[/math] drawn to side [math]\displaystyle{ a. }[/math] Let [math]\displaystyle{ m }[/math] be the length of the segments of [math]\displaystyle{ a }[/math] formed by the median, so [math]\displaystyle{ m }[/math] is half of [math]\displaystyle{ a. }[/math] Let the angles formed between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ d }[/math] be [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \theta^{\prime}, }[/math] where [math]\displaystyle{ \theta }[/math] includes [math]\displaystyle{ b }[/math] and [math]\displaystyle{ \theta^{\prime} }[/math] includes [math]\displaystyle{ c. }[/math] Then [math]\displaystyle{ \theta^{\prime} }[/math] is the supplement of [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \cos \theta^{\prime} = - \cos \theta. }[/math] The law of cosines for [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \theta^{\prime} }[/math] states that [math]\displaystyle{ \begin{align} b^2 &= m^2 + d^2 - 2dm\cos\theta \\ c^2 &= m^2 + d^2 - 2dm\cos\theta' \\ &= m^2 + d^2 + 2dm\cos\theta.\, \end{align} }[/math]
Add the first and third equations to obtain [math]\displaystyle{ b^2 + c^2 = 2(m^2 + d^2) }[/math] as required.
See also
References
- ↑ Godfrey, Charles; Siddons, Arthur Warry (1908). Modern Geometry. University Press. p. 20. https://archive.org/details/bub_gb_LGsLAAAAYAAJ.
External links
- Apollonius Theorem at PlanetMath.org.
- David B. Surowski: Advanced High-School Mathematics. p. 27
 |