Simplicial depth

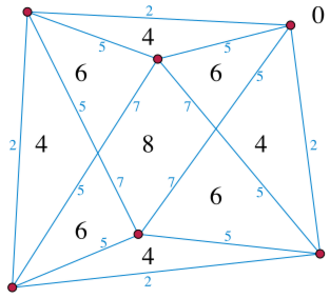
Simplicial depth with respect to the six red sample points, using the modified definition of Burr et al. The large black numbers are the depths within each region, and the small blue numbers are the depths along the blue line segments.

In robust statistics and computational geometry, simplicial depth is a measure of central tendency determined by the simplices that contain a given point. For the Euclidean plane, it counts the number of triangles of sample points that contain a given point.

Definition

The simplicial depth of a point [math]\displaystyle{ p }[/math] in [math]\displaystyle{ d }[/math]-dimensional Euclidean space, with respect to a set of sample points in that space, is the number of [math]\displaystyle{ d }[/math]-dimensional simplices (the convex hulls of sets of [math]\displaystyle{ d+1 }[/math] sample points) that contain [math]\displaystyle{ p }[/math]. The same notion can be generalized to any probability distribution on points of the plane, not just the empirical distribution given by a set of sample points, by defining the depth to be the probability that a randomly chosen [math]\displaystyle{ (d+1) }[/math]-tuple of points has a convex hull that contains [math]\displaystyle{ p }[/math]. This probability can be calculated, from the number of simplices that contain [math]\displaystyle{ p }[/math], by dividing by [math]\displaystyle{ \tbinom{n}{d+1} }[/math] where [math]\displaystyle{ n }[/math] is the number of sample points.

Under the standard definition of simplicial depth, the simplices that have [math]\displaystyle{ p }[/math] on their boundaries count equally much as the simplices with [math]\displaystyle{ p }[/math] in their interiors. In order to avoid some problematic behavior of this definition, (Burr Rafalin) proposed a modified definition of simplicial depth, in which the simplices with [math]\displaystyle{ p }[/math] on their boundaries count only half as much. Equivalently, their definition is the average of the number of open simplices and the number of closed simplices that contain [math]\displaystyle{ p }[/math].

Properties

Simplicial depth is robust against outliers: if a set of sample points is represented by the point of maximum depth, then up to a constant fraction of the sample points can be arbitrarily corrupted without significantly changing the location of the representative point. It is also invariant under affine transformations of the plane.

However, simplicial depth fails to have some other desirable properties for robust measures of central tendency. When applied to centrally symmetric distributions, it is not necessarily the case that there is a unique point of maximum depth in the center of the distribution. And, along a ray from the point of maximum depth, it is not necessarily the case that the simplicial depth decreases monotonically.

Algorithms

For sets of [math]\displaystyle{ n }[/math] sample points in the Euclidean plane ([math]\displaystyle{ d=2 }[/math]), the simplicial depth of any other point [math]\displaystyle{ p }[/math] can be computed in time [math]\displaystyle{ O(n\log n) }[/math], optimal in some models of computation. In three dimensions, the same problem can be solved in time [math]\displaystyle{ O(n^2) }[/math].

It possible to construct a data structure using ε-nets that can approximate the simplicial depth of a query point (given either a fixed set of samples, or a set of samples undergoing point insertions) in near-constant time per query, in any dimension, with an approximation whose error is a small fraction of the total number of triangles determined by the samples. In two dimensions, a more accurate approximation algorithm is known, for which the approximation error is a small multiple of the simplicial depth itself. The same methods also lead to fast approximation algorithms in higher dimensions.

Spherical depth, [math]\displaystyle{ SphD(q; F) }[/math] is defined to be the probability that a point [math]\displaystyle{ q }[/math] is contained inside a random closed hyperball obtained from a pair of points from [math]\displaystyle{ F \in \mathbb{R}^n }[/math]. While the time complexity of most other data depths grows exponentially, the spherical depth grows only linearly in the dimension [math]\displaystyle{ d }[/math] – the straightforward algorithm for computing the spherical depth takes [math]\displaystyle{ O(dn^2) }[/math]. Simplicial depth (SD) is linearly bounded by spherical depth ([math]\displaystyle{ SphD \ge \frac{2}{3}SD }[/math]).

References

ASS. Afshani, Peyman; Sheehy, Donald R.; Stein, Yannik (2015), Approximating the simplicial depth, Bibcode: 2015arXiv151204856A 

ACG. Aloupis, Greg; Cortés, Carmen; Gómez, Francisco; Soss, Michael (2002), "Lower bounds for computing statistical depth", Computational Statistics & Data Analysis 40 (2): 223–229, doi:10.1016/S0167-9473(02)00032-4 

BCE. Bagchi, Amitabha; Chaudhary, Amitabh (2007), "Deterministic sampling and range counting in geometric data streams", ACM Transactions on Algorithms 3 (2): Art. 16, 18, doi:10.1145/1240233.1240239 

BRS. Burr, Michael A.; Rafalin, Eynat (2004), "Simplicial depth: An improved definition, analysis, and efficiency for the finite sample case", Proceedings of the 16th Canadian Conference on Computational Geometry, CCCG'04, Concordia University, Montréal, Québec, Canada, August 9-11, 2004, pp. 136–139, http://www.cccg.ca/proceedings/2004/49.pdf 

BS. Bremner, David; Shahsavarifar, Rasoul (2017), An Optimal Algorithm for Computing the Spherical Depth of Points in the Plane, Bibcode: 2017arXiv170207399B 

CO. Cheng, Andrew Y.; Ouyang, Ming (2001), "On algorithms for simplicial depth", Proceedings of the 13th Canadian Conference on Computational Geometry, University of Waterloo, Ontario, Canada, August 13-15, 2001, pp. 53–56, http://www.cccg.ca/proceedings/2001/ouyang-24534.ps.gz 

D. Dümbgen, Lutz (1992), "Limit theorems for the simplicial depth", Statistics & Probability Letters 14 (2): 119–128, doi:10.1016/0167-7152(92)90075-G 

GSW. Gil, Joseph; Steiger, William (1992), "Geometric medians", Discrete Mathematics 108 (1–3): 37–51, doi:10.1016/0012-365X(92)90658-3 

KM. "On a triangle counting problem", Information Processing Letters 33 (6): 319–321, 1990, doi:10.1016/0020-0190(90)90217-L 

L88. "On a notion of simplicial depth", Proceedings of the National Academy of Sciences of the United States of America 85 (6): 1732–1734, 1988, doi:10.1073/pnas.85.6.1732, PMID 16578830, Bibcode: 1988PNAS...85.1732L 

L90. "On a notion of data depth based on random simplices", Annals of Statistics 18 (1): 405–414, 1990, doi:10.1214/aos/1176347507 

RR. "Algorithm AS 307: Bivariate Location Depth", Applied Statistics 45 (4): 516, 1996, doi:10.2307/2986073 

ZS. Zuo, Yijun; Serfling, Robert (2000), "General notions of statistical depth function", Annals of Statistics 28 (2): 461–482, doi:10.1214/aos/1016218226