Empirical distribution function
In statistics, an empirical distribution function (commonly also called an empirical cumulative distribution function, eCDF) is the distribution function associated with the empirical measure of a sample.[1] This cumulative distribution function is a step function that jumps up by 1/n at each of the n data points. Its value at any specified value of the measured variable is the fraction of observations of the measured variable that are less than or equal to the specified value.
The empirical distribution function is an estimate of the cumulative distribution function that generated the points in the sample. It converges with probability 1 to that underlying distribution, according to the Glivenko–Cantelli theorem. A number of results exist to quantify the rate of convergence of the empirical distribution function to the underlying cumulative distribution function.
Definition
Let (X1, …, Xn) be independent, identically distributed real random variables with the common cumulative distribution function F(t). Then the empirical distribution function is defined as[2]
- [math]\displaystyle{ \widehat F_n(t) = \frac{\mbox{number of elements in the sample} \leq t}{n} = \frac{1}{n} \sum_{i=1}^n \mathbf{1}_{X_i \le t}, }[/math]
where [math]\displaystyle{ \mathbf{1}_{A} }[/math] is the indicator of event A. For a fixed t, the indicator [math]\displaystyle{ \mathbf{1}_{X_i \le t} }[/math] is a Bernoulli random variable with parameter p = F(t); hence [math]\displaystyle{ n \widehat F_n(t) }[/math] is a binomial random variable with mean nF(t) and variance nF(t)(1 − F(t)). This implies that [math]\displaystyle{ \widehat F_n(t) }[/math] is an unbiased estimator for F(t).
However, in some textbooks, the definition is given as
- [math]\displaystyle{ \widehat F_n(t) = \frac{1}{n+1} \sum_{i=1}^n \mathbf{1}_{X_i \le t} }[/math][3][4]
Mean
The mean of the empirical distribution is an unbiased estimator of the mean of the population distribution.
- [math]\displaystyle{ E_n(X) = \frac{1}{n}\left (\sum_{i=1}^n{x_i}\right ) }[/math]
which is more commonly denoted [math]\displaystyle{ \bar{x} }[/math]
Variance
The variance of the empirical distribution times [math]\displaystyle{ \tfrac{n}{n-1} }[/math] is an unbiased estimator of the variance of the population distribution, for any distribution of X that has a finite variance.
- [math]\displaystyle{ \begin{align} \operatorname{Var}(X) &= \operatorname{E}\left[(X - \operatorname{E}[X])^2\right] \\[4pt] &= \operatorname{E}\left[(X - \bar{x})^2\right] \\[4pt] &= \frac{1}{n}\left (\sum_{i=1}^n{(x_i-\bar{x})^2}\right ) \end{align} }[/math]
Mean squared error
The mean squared error for the empirical distribution is as follows.
- [math]\displaystyle{ \begin{align} \operatorname{MSE}&=\frac{1}{n}\sum_{i=1}^n(Y_i-\hat{Y_i})^2\\[4pt] &=\operatorname{Var}_{\hat\theta}(\hat{\theta})+ \operatorname{Bias}(\hat{\theta},\theta)^2 \end{align} }[/math]
Where [math]\displaystyle{ \hat{\theta} }[/math] is an estimator and [math]\displaystyle{ \theta }[/math] an unknown parameter
Quantiles
For any real number [math]\displaystyle{ a }[/math] the notation [math]\displaystyle{ \lceil{a}\rceil }[/math] (read “ceiling of a”) denotes the least integer greater than or equal to [math]\displaystyle{ a }[/math]. For any real number a, the notation [math]\displaystyle{ \lfloor{a}\rfloor }[/math] (read “floor of a”) denotes the greatest integer less than or equal to [math]\displaystyle{ a }[/math].
If [math]\displaystyle{ nq }[/math] is not an integer, then the [math]\displaystyle{ q }[/math]-th quantile is unique and is equal to [math]\displaystyle{ x_{(\lceil{nq}\rceil)} }[/math]
If [math]\displaystyle{ nq }[/math] is an integer, then the [math]\displaystyle{ q }[/math]-th quantile is not unique and is any real number [math]\displaystyle{ x }[/math] such that
- [math]\displaystyle{ x_{({nq})}\lt x\lt x_{({nq+1})} }[/math]
Empirical median
If [math]\displaystyle{ n }[/math] is odd, then the empirical median is the number
- [math]\displaystyle{ \tilde{x} = x_{(\lceil{n/2}\rceil)} }[/math]
If [math]\displaystyle{ n }[/math] is even, then the empirical median is the number
- [math]\displaystyle{ \tilde{x} =\frac{ x_{n/2} + x_{n/2+1}}{2} }[/math]
Asymptotic properties
Since the ratio (n + 1)/n approaches 1 as n goes to infinity, the asymptotic properties of the two definitions that are given above are the same.
By the strong law of large numbers, the estimator [math]\displaystyle{ \scriptstyle\widehat{F}_n(t) }[/math] converges to F(t) as n → ∞ almost surely, for every value of t:[2]
- [math]\displaystyle{ \widehat F_n(t)\ \xrightarrow{\text{a.s.}}\ F(t); }[/math]
thus the estimator [math]\displaystyle{ \scriptstyle\widehat{F}_n(t) }[/math] is consistent. This expression asserts the pointwise convergence of the empirical distribution function to the true cumulative distribution function. There is a stronger result, called the Glivenko–Cantelli theorem, which states that the convergence in fact happens uniformly over t:[5]
- [math]\displaystyle{ \|\widehat F_n-F\|_\infty \equiv \sup_{t\in\mathbb{R}} \big|\widehat F_n(t)-F(t)\big|\ \xrightarrow{\text{a.s.}}\ 0. }[/math]
The sup-norm in this expression is called the Kolmogorov–Smirnov statistic for testing the goodness-of-fit between the empirical distribution [math]\displaystyle{ \scriptstyle\widehat{F}_n(t) }[/math] and the assumed true cumulative distribution function F. Other norm functions may be reasonably used here instead of the sup-norm. For example, the L2-norm gives rise to the Cramér–von Mises statistic.
The asymptotic distribution can be further characterized in several different ways. First, the central limit theorem states that pointwise, [math]\displaystyle{ \scriptstyle\widehat{F}_n(t) }[/math] has asymptotically normal distribution with the standard [math]\displaystyle{ \sqrt{n} }[/math] rate of convergence:[2]
- [math]\displaystyle{ \sqrt{n}\big(\widehat F_n(t) - F(t)\big)\ \ \xrightarrow{d}\ \ \mathcal{N}\Big( 0, F(t)\big(1-F(t)\big) \Big). }[/math]
This result is extended by the Donsker’s theorem, which asserts that the empirical process [math]\displaystyle{ \scriptstyle\sqrt{n}(\widehat{F}_n - F) }[/math], viewed as a function indexed by [math]\displaystyle{ \scriptstyle t\in\mathbb{R} }[/math], converges in distribution in the Skorokhod space [math]\displaystyle{ \scriptstyle D[-\infty, +\infty] }[/math] to the mean-zero Gaussian process [math]\displaystyle{ \scriptstyle G_F = B \circ F }[/math], where B is the standard Brownian bridge.[5] The covariance structure of this Gaussian process is
- [math]\displaystyle{ \operatorname{E}[\,G_F(t_1)G_F(t_2)\,] = F(t_1\wedge t_2) - F(t_1)F(t_2). }[/math]
The uniform rate of convergence in Donsker’s theorem can be quantified by the result known as the Hungarian embedding:[6]
- [math]\displaystyle{ \limsup_{n\to\infty} \frac{\sqrt{n}}{\ln^2 n} \big\| \sqrt{n}(\widehat F_n-F) - G_{F,n}\big\|_\infty \lt \infty, \quad \text{a.s.} }[/math]
Alternatively, the rate of convergence of [math]\displaystyle{ \scriptstyle\sqrt{n}(\widehat{F}_n-F) }[/math] can also be quantified in terms of the asymptotic behavior of the sup-norm of this expression. Number of results exist in this venue, for example the Dvoretzky–Kiefer–Wolfowitz inequality provides bound on the tail probabilities of [math]\displaystyle{ \scriptstyle\sqrt{n}\|\widehat{F}_n-F\|_\infty }[/math]:[6]
- [math]\displaystyle{ \Pr\!\Big( \sqrt{n}\|\widehat{F}_n-F\|_\infty \gt z \Big) \leq 2e^{-2z^2}. }[/math]
In fact, Kolmogorov has shown that if the cumulative distribution function F is continuous, then the expression [math]\displaystyle{ \scriptstyle\sqrt{n}\|\widehat{F}_n-F\|_\infty }[/math] converges in distribution to [math]\displaystyle{ \scriptstyle\|B\|_\infty }[/math], which has the Kolmogorov distribution that does not depend on the form of F.
Another result, which follows from the law of the iterated logarithm, is that [6]
- [math]\displaystyle{ \limsup_{n\to\infty} \frac{\sqrt{n}\|\widehat{F}_n-F\|_\infty}{\sqrt{2\ln\ln n}} \leq \frac12, \quad \text{a.s.} }[/math]
and
- [math]\displaystyle{ \liminf_{n\to\infty} \sqrt{2n\ln\ln n} \|\widehat{F}_n-F\|_\infty = \frac{\pi}{2}, \quad \text{a.s.} }[/math]
Confidence intervals
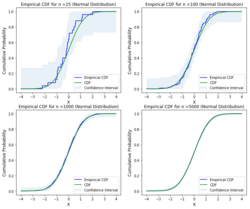
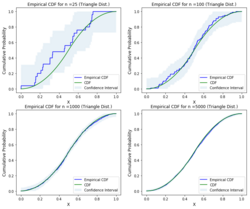
As per Dvoretzky–Kiefer–Wolfowitz inequality the interval that contains the true CDF, [math]\displaystyle{ F(x) }[/math], with probability [math]\displaystyle{ 1-\alpha }[/math] is specified as
- [math]\displaystyle{ F_n(x) - \varepsilon \le F(x) \le F_n(x) + \varepsilon \; \text{ where } \varepsilon = \sqrt{\frac{\ln{\frac{2}{\alpha}}}{2n}}. }[/math]
As per the above bounds, we can plot the Empirical CDF, CDF and confidence intervals for different distributions by using any one of the statistical implementations.
Statistical implementation
A non-exhaustive list of software implementations of Empirical Distribution function includes:
- In R software, we compute an empirical cumulative distribution function, with several methods for plotting, printing and computing with such an “ecdf” object.
- In MATLAB we can use Empirical cumulative distribution function (cdf) plot
- jmp from SAS, the CDF plot creates a plot of the empirical cumulative distribution function.
- Minitab, create an Empirical CDF
- Mathwave, we can fit probability distribution to our data
- Dataplot, we can plot Empirical CDF plot
- Scipy, we can use scipy.stats.ecdf
- Statsmodels, we can use statsmodels.distributions.empirical_distribution.ECDF
- Matplotlib, using the matplotlib.pyplot.ecdf function (new in version 3.8.0)[7]
- Seaborn, using the seaborn.ecdfplot function
- Plotly, using the plotly.express.ecdf function
- Excel, we can plot Empirical CDF plot
- ArviZ, using the az.plot_ecdf function
See also
- Càdlàg functions
- Count data
- Distribution fitting
- Dvoretzky–Kiefer–Wolfowitz inequality
- Empirical probability
- Empirical process
- Estimating quantiles from a sample
- Frequency (statistics)
- Empirical likelihood
- Kaplan–Meier estimator for censored processes
- Survival function
- Q–Q plot
References
- ↑ A modern introduction to probability and statistics: Understanding why and how. Michel Dekking. London: Springer. 2005. pp. 219. ISBN 978-1-85233-896-1. OCLC 262680588. https://www.worldcat.org/oclc/262680588.
- ↑ 2.0 2.1 2.2 van der Vaart, A.W. (1998). Asymptotic statistics. Cambridge University Press. p. 265. ISBN 0-521-78450-6. https://archive.org/details/asymptoticstatis00vaar_017.
- ↑ Coles, S. (2001) An Introduction to Statistical Modeling of Extreme Values. Springer, p. 36, Definition 2.4. ISBN:978-1-4471-3675-0.
- ↑ Madsen, H.O., Krenk, S., Lind, S.C. (2006) Methods of Structural Safety. Dover Publications. p. 148-149. ISBN:0486445976
- ↑ 5.0 5.1 van der Vaart, A.W. (1998). Asymptotic statistics. Cambridge University Press. p. 266. ISBN 0-521-78450-6. https://archive.org/details/asymptoticstatis00vaar_017.
- ↑ 6.0 6.1 6.2 van der Vaart, A.W. (1998). Asymptotic statistics. Cambridge University Press. p. 268. ISBN 0-521-78450-6. https://archive.org/details/asymptoticstatis00vaar_017.
- ↑ https://matplotlib.org/stable/users/prev_whats_new/whats_new_3.8.0.html#axes-ecdf
Further reading
- Empirical Processes with Applications to Statistics. New York: Wiley. 1986. ISBN 0-471-86725-X.
External links
 |  |
