D4 polytope
In 4-dimensional geometry, there are 7 uniform 4-polytopes with reflections of D4 symmetry, all are shared with higher symmetry constructions in the B4 or F4 symmetry families. there is also one half symmetry alternation, the snub 24-cell.
Visualizations
Each can be visualized as symmetric orthographic projections in Coxeter planes of the D4 Coxeter group, and other subgroups. The B4 coxeter planes are also displayed, while D4 polytopes only have half the symmetry. They can also be shown in perspective projections of Schlegel diagrams, centered on different cells.
| index | Name Coxeter diagram |
Coxeter plane projections | Schlegel diagrams | Net | |||
|---|---|---|---|---|---|---|---|
| B4 [8] |
D4, B3 [6] |
D3, B2 [4] |
Cube centered |
Tetrahedron centered | |||
| 1 | demitesseract (Same as 16-cell) {3,31,1} |
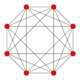
|
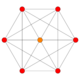
|
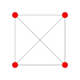
|
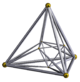
|

| |
| 2 | cantic tesseract (Same as truncated 16-cell) t{3,31,1} |

|
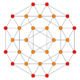
|
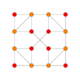
|
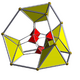
|
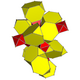
| |
| 3 | runcic tesseract birectified 16-cell (Same as rectified tesseract) 2r{3,31,1} |
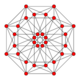
|
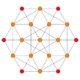
|

|

|
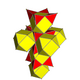
| |
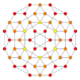
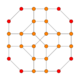
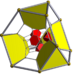
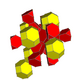
| 4 | runcicantic tesseract bitruncated 16-cell (Same as bitruncated tesseract) 2t{3,31,1} |
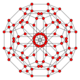
|
|
|
|
| |
| index | Name Coxeter diagram |
Coxeter plane projections | Schlegel diagrams | Parallel 3D |
Net | ||||
|---|---|---|---|---|---|---|---|---|---|
| F4 [12] |
B4 [8] |
D4, B3 [6] |
D3, B2 [2] |
Cube centered |
Tetrahedron centered |
D4 [6] | |||
| 5 | rectified 16-cell (Same as 24-cell) {31,1,1} = r{3,3,4} = {3,4,3} |
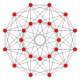
|
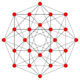
|
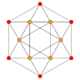
|
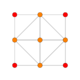
|
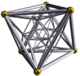
|

| ||
| 6 | cantellated 16-cell (Same as rectified 24-cell) r{31,1,1} = rr{3,3,4} = r{3,4,3} |

|
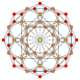
|
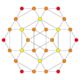
|

|

|
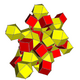
| ||
| 7 | cantitruncated 16-cell (Same as truncated 24-cell) t{31,1,1} = tr{3,31,1} = tr{3,3,4} = t{3,4,3} |

|
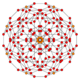
|
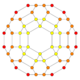
|
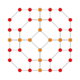
|

|
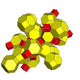
| ||
| 8 | (Same as snub 24-cell) s{31,1,1} = sr{3,31,1} = sr{3,3,4} = s{3,4,3} |

|
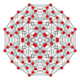
|
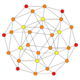
|

|

|

| ||
Coordinates
The base point can generate the coordinates of the polytope by taking all coordinate permutations and sign combinations. The edges' length will be √2. Some polytopes have two possible generator points. Points are prefixed by Even to imply only an even count of sign permutations should be included.
| # | Name(s) | Base point | Johnson | Coxeter diagrams | ||
|---|---|---|---|---|---|---|
| D4 | B4 | F4 | ||||
| 1 | hγ4 | Even (1,1,1,1) | demitesseract | |||
| 3 | h3γ4 | Even (1,1,1,3) | runcic tesseract | |||
| 2 | h2γ4 | Even (1,1,3,3) | cantic tesseract | |||
| 4 | h2,3γ4 | Even (1,3,3,3) | runcicantic tesseract | |||
| 1 | t3γ4 = β4 | (0,0,0,2) | 16-cell | |||
| 5 | t2γ4 = t1β4 | (0,0,2,2) | rectified 16-cell | |||
| 2 | t2,3γ4 = t0,1β4 | (0,0,2,4) | truncated 16-cell | |||
| 6 | t1γ4 = t2β4 | (0,2,2,2) | cantellated 16-cell | |||
| 9 | t1,3γ4 = t0,2β4 | (0,2,2,4) | cantellated 16-cell | |||
| 7 | t1,2,3γ = t0,1,2β4 | (0,2,4,6) | cantitruncated 16-cell | |||
| 8 | s{31,1,1} | (0,1,φ,φ+1)/√2 | Snub 24-cell | |||
References
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
External links
- Klitzing, Richard. "4D uniform 4-polytopes". https://bendwavy.org/klitzing/dimensions/polychora.htm.
- Uniform, convex polytopes in four dimensions:, Marco Möller (in German)
- Möller, Marco (2004). Vierdimensionale Archimedische Polytope (PDF) (Doctoral dissertation) (in Deutsch). University of Hamburg.
- Uniform Polytopes in Four Dimensions, George Olshevsky.
- Convex uniform polychora based on the tesseract/16-cell, George Olshevsky.
- Convex uniform polychora based on the 24-cell, George Olshevsky.
- Uniform polychora derived from B4 (D4), George Olshevsky.
 |

