Orthographic projection
| Part of a series on |
| Graphical projection |
|---|
 |
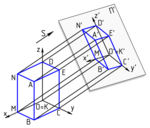Orthographic projection (also orthogonal projection and analemma)[lower-alpha 1] is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane,[2] resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are not orthogonal to the projection plane.
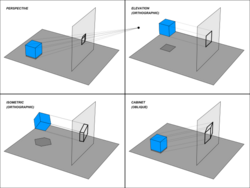
The term orthographic sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the primary views.[2] If the principal planes or axes of an object in an orthographic projection are not parallel with the projection plane, the depiction is called axonometric or an auxiliary views. (Axonometric projection is synonymous with parallel projection.) Sub-types of primary views include plans, elevations, and sections; sub-types of auxiliary views include isometric, dimetric, and trimetric projections.
A lens that provides an orthographic projection is an object-space telecentric lens.
Geometry
A simple orthographic projection onto the plane z = 0 can be defined by the following matrix:
- [math]\displaystyle{ P = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} }[/math]
For each point v = (vx, vy, vz), the transformed point Pv would be
- [math]\displaystyle{ Pv = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix} = \begin{bmatrix} v_x \\ v_y \\ 0 \end{bmatrix} }[/math]
Often, it is more useful to use homogeneous coordinates. The transformation above can be represented for homogeneous coordinates as
- [math]\displaystyle{ P = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]
For each homogeneous vector v = (vx, vy, vz, 1), the transformed vector Pv would be
- [math]\displaystyle{ Pv = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 1 \end{bmatrix} = \begin{bmatrix} v_x \\ v_y \\ 0 \\ 1 \end{bmatrix} }[/math]
In computer graphics, one of the most common matrices used for orthographic projection can be defined by a 6-tuple, (left, right, bottom, top, near, far), which defines the clipping planes. These planes form a box with the minimum corner at (left, bottom, -near) and the maximum corner at (right, top, -far).[3]
The box is translated so that its center is at the origin, then it is scaled to the unit cube which is defined by having a minimum corner at (−1,−1,−1) and a maximum corner at (1,1,1).
The orthographic transform can be given by the following matrix:
- [math]\displaystyle{ P = \begin{bmatrix} \frac{2}{\text{right}-\text{left}} & 0 & 0 & -\frac{\text{right}+\text{left}}{\text{right}-\text{left}} \\ 0 & \frac{2}{\text{top}-\text{bottom}} & 0 & -\frac{\text{top}+\text{bottom}}{\text{top}-\text{bottom}} \\ 0 & 0 & \frac{-2}{\text{far}-\text{near}} & -\frac{\text{far}+\text{near}}{\text{far}-\text{near}} \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]
which can be given as a scaling S followed by a translation T of the form
- [math]\displaystyle{ P = ST = \begin{bmatrix} \frac{2}{\text{right}-\text{left}} & 0 & 0 & 0 \\ 0 & \frac{2}{\text{top}-\text{bottom}} & 0 & 0 \\ 0 & 0 & \frac{2}{\text{far}-\text{near}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{\text{left}+\text{right}}{2} \\ 0 & 1 & 0 & -\frac{\text{top}+\text{bottom}}{2} \\ 0 & 0 & -1 & -\frac{\text{far}+\text{near}}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]
The inversion of the projection matrix P−1, which can be used as the unprojection matrix is defined:
[math]\displaystyle{ P^{-1} = \begin{bmatrix} \frac{\text{right}-\text{left}}{2} & 0 & 0 & \frac{\text{left}+\text{right}}{2} \\ 0 & \frac{\text{top}-\text{bottom}}{2} & 0 & \frac{\text{top}+\text{bottom}}{2} \\ 0 & 0 & \frac{\text{far}-\text{near}}{-2} & -\frac{\text{far}+\text{near}}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} }[/math]
Types
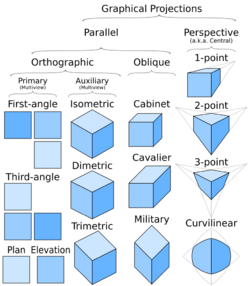
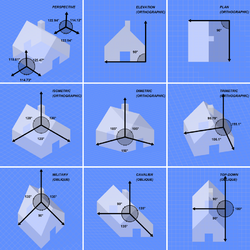
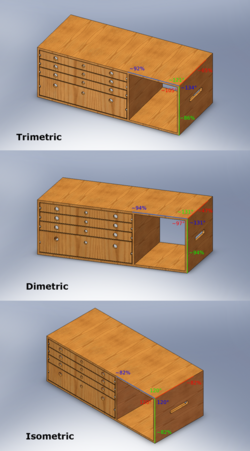
Three sub-types of orthographic projection are isometric projection, dimetric projection, and trimetric projection, depending on the exact angle at which the view deviates from the orthogonal.[2][4] Typically in axonometric drawing, as in other types of pictorials, one axis of space is shown to be vertical.
In isometric projection, the most commonly used form of axonometric projection in engineering drawing,[5] the direction of viewing is such that the three axes of space appear equally foreshortened, and there is a common angle of 120° between them. As the distortion caused by foreshortening is uniform, the proportionality between lengths is preserved, and the axes share a common scale; this eases one's ability to take measurements directly from the drawing. Another advantage is that 120° angles are easily constructed using only a compass and straightedge.
In dimetric projection, the direction of viewing is such that two of the three axes of space appear equally foreshortened, of which the attendant scale and angles of presentation are determined according to the angle of viewing; the scale of the third direction is determined separately. Dimensional approximations are common in dimetric drawings.[clarification needed]
In trimetric projection, the direction of viewing is such that all of the three axes of space appear unequally foreshortened. The scale along each of the three axes and the angles among them are determined separately as dictated by the angle of viewing. Dimensional approximations in trimetric drawings are common,[clarification needed] and trimetric perspective is seldom used in technical drawings.[4]
Multiview projection
In multiview projection, up to six pictures of an object are produced, called primary views, with each projection plane parallel to one of the coordinate axes of the object. The views are positioned relative to each other according to either of two schemes: first-angle or third-angle projection. In each, the appearances of views may be thought of as being projected onto planes that form a six-sided box around the object. Although six different sides can be drawn, usually three views of a drawing give enough information to make a three-dimensional object. These views are known as front view (also elevation), top view (also plan) and end view (also section). When the plane or axis of the object depicted is not parallel to the projection plane, and where multiple sides of an object are visible in the same image, it is called an auxiliary view. Thus isometric projection, dimetric projection and trimetric projection would be considered auxiliary views in multiview projection. A typical characteristic of multiview projection is that one axis of space is usually displayed as vertical.
Cartography
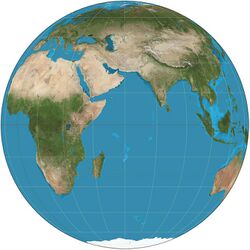
An orthographic projection map is a map projection of cartography. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective (or azimuthal) projection, in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic projection is at infinite distance. It depicts a hemisphere of the globe as it appears from outer space, where the horizon is a great circle. The shapes and areas are distorted, particularly near the edges.[6][7]
The orthographic projection has been known since antiquity, with its cartographic uses being well documented. Hipparchus used the projection in the 2nd century BC to determine the places of star-rise and star-set. In about 14 BC, Roman engineer Marcus Vitruvius Pollio used the projection to construct sundials and to compute sun positions.[7]
Vitruvius also seems to have devised the term orthographic – from the Greek orthos ("straight") and graphē ("drawing") – for the projection. However, the name analemma, which also meant a sundial showing latitude and longitude, was the common name until François d'Aguilon of Antwerp promoted its present name in 1613.[7]
The earliest surviving maps on the projection appear as woodcut drawings of terrestrial globes of 1509 (anonymous), 1533 and 1551 (Johannes Schöner), and 1524 and 1551 (Apian).[7]
Notes
References
- ↑ Sawyer, F., Of Analemmas, Mean Time and the Analemmatic Sundial
- ↑ 2.0 2.1 2.2 Maynard, Patric (2005). Drawing Distinctions: The Varieties of Graphic Expression. Cornell University Press. pp. 22. ISBN 0-8014-7280-6. https://books.google.com/books?id=4Y_YqOlXoxMC&q=axonometric%20orthographic&pg=PA22.
- ↑ Thormählen, Thorsten (November 26, 2021). "Graphics Programming – Cameras: Parallel Projection – Part 6, Chapter 2". pp. 8 ff. https://www.mathematik.uni-marburg.de/~thormae/lectures/graphics1/graphics_6_2_eng_web.html#10.
- ↑ 4.0 4.1 McReynolds, Tom; David Blythe (2005). Advanced graphics programming using openGL. Elsevier. pp. 502. ISBN 1-55860-659-9. https://books.google.com/books?id=bmv2HRpG1bUC&q=axonometric.
- ↑ Godse, Atul P. (1984). Computer graphics. Technical Publications. pp. 29. ISBN 81-8431-558-9. https://books.google.com/books?id=YkVp-2ZrmyMC&q=axonometric+orthographic&pg=PT224.
- ↑ Snyder, J. P. (1987). Map Projections—A Working Manual (US Geologic Survey Professional Paper 1395). Washington, D.C.: US Government Printing Office. pp. 145–153.
- ↑ 7.0 7.1 7.2 7.3 Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections pp. 16–18. Chicago and London: The University of Chicago Press. ISBN:0-226-76746-9.
External links
de:Orthogonale Projektion#Orthogonale Projektion
 |  |
