24-cell
- REDIRECT Template:Infobox 4-polytope
This page is a redirect. The following categories are used to track and monitor this redirect:
|
In four-dimensional geometry, the 24-cell is the convex regular 4-polytope[1] (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,4,3}. It is also called C24, or the icositetrachoron,[2] octaplex (short for "octahedral complex"), icosatetrahedroid,[3] octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.
The boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex figure is a cube. The 24-cell is self-dual.[lower-alpha 1] The 24-cell and the tesseract are the only convex regular 4-polytopes in which the edge length equals the radius.[lower-alpha 2]
The 24-cell does not have a regular analogue in 3 dimensions. It is the only one of the six convex regular 4-polytopes which is not the four-dimensional analogue of one of the five regular Platonic solids. It is the unique regular polytope, in any number of dimensions, which has no regular analogue in the adjacent dimension, either below or above.[4] However, it can be seen as the analogue of a pair of irregular solids: the cuboctahedron and its dual the rhombic dodecahedron.[5]
Translated copies of the 24-cell can tile four-dimensional space face-to-face, forming the 24-cell honeycomb. As a polytope that can tile by translation, the 24-cell is an example of a parallelotope, the simplest one that is not also a zonotope.[6]
Geometry
The 24-cell incorporates the geometries of every convex regular polytope in the first four dimensions, except the 5-cell, those with a 5 in their Schlӓfli symbol,[lower-alpha 3] and the regular polygons with 7 or more sides. It is especially useful to explore the 24-cell, because one can see the geometric relationships among all of these regular polytopes in a single 24-cell or its honeycomb.
The 24-cell is the fourth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).[lower-alpha 4] It can be deconstructed into 3 overlapping instances of its predecessor the tesseract (8-cell), as the 8-cell can be deconstructed into 2 overlapping instances of its predecessor the 16-cell.[8] The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length.[lower-alpha 5]
Coordinates
Squares
The 24-cell is the convex hull of its vertices which can be described as the 24 coordinate permutations of:
[math]\displaystyle{ (\pm1, \pm 1, 0, 0) \in \mathbb{R}^4 . }[/math]
Those coordinates[9] can be constructed as ![]()
![]()
![]()
![]()
![]()
![]()
![]() , rectifying the 16-cell
, rectifying the 16-cell ![]()
![]()
![]()
![]()
![]()
![]()
![]() with 8 vertices permutations of (±2,0,0,0). The vertex figure of a 16-cell is the octahedron; thus, cutting the vertices of the 16-cell at the midpoint of its incident edges produces 8 octahedral cells. This process[10] also rectifies the tetrahedral cells of the 16-cell which become 16 octahedra, giving the 24-cell 24 octahedral cells.
with 8 vertices permutations of (±2,0,0,0). The vertex figure of a 16-cell is the octahedron; thus, cutting the vertices of the 16-cell at the midpoint of its incident edges produces 8 octahedral cells. This process[10] also rectifies the tetrahedral cells of the 16-cell which become 16 octahedra, giving the 24-cell 24 octahedral cells.
In this frame of reference the 24-cell has edges of length √2 and is inscribed in a 3-sphere of radius √2. Remarkably, the edge length equals the circumradius, as in the hexagon, or the cuboctahedron. Such polytopes are radially equilateral.[lower-alpha 2]
Template:Regular convex 4-polytopes
The 24 vertices form 18 great squares[lower-alpha 6] (3 sets of 6 orthogonal[lower-alpha 8] central squares), 3 of which intersect at each vertex. By viewing just one square at each vertex, the 24-cell can be seen as the vertices of 3 pairs of completely orthogonal[lower-alpha 7] great squares which intersect[lower-alpha 11] at no vertices.[lower-alpha 12]
Hexagons
The 24-cell is self-dual, having the same number of vertices (24) as cells and the same number of edges (96) as faces.
If the dual of the above 24-cell of edge length √2 is taken by reciprocating it about its inscribed sphere, another 24-cell is found which has edge length and circumradius 1, and its coordinates reveal more structure. In this frame of reference the 24-cell lies vertex-up, and its vertices can be given as follows:
8 vertices obtained by permuting the integer coordinates:
[math]\displaystyle{ \left( \pm 1, 0, 0, 0 \right) }[/math]
and 16 vertices with half-integer coordinates of the form:
[math]\displaystyle{ \left( \pm \tfrac{1}{2}, \pm \tfrac{1}{2}, \pm \tfrac{1}{2}, \pm \tfrac{1}{2} \right) }[/math]
all 24 of which lie at distance 1 from the origin.
Viewed as quaternions,[lower-alpha 13] these are the unit Hurwitz quaternions.
The 24-cell has unit radius and unit edge length[lower-alpha 2] in this coordinate system. We refer to the system as unit radius coordinates to distinguish it from others, such as the √2 radius coordinates used above.[lower-alpha 14]
The 24 vertices and 96 edges form 16 non-orthogonal great hexagons,[lower-alpha 17] four of which intersect[lower-alpha 11] at each vertex.[lower-alpha 19] By viewing just one hexagon at each vertex, the 24-cell can be seen as the 24 vertices of 4 non-intersecting hexagonal great circles which are Clifford parallel to each other.[lower-alpha 20]
The 12 axes and 16 hexagons of the 24-cell constitute a Reye configuration, which in the language of configurations is written as 124163 to indicate that each axis belongs to 4 hexagons, and each hexagon contains 3 axes.[11]
Triangles
The 24 vertices form 32 equilateral great triangles, of edge length √3 in the unit-radius 24-cell,[lower-alpha 23] inscribed in the 16 great hexagons.[lower-alpha 24] Each great triangle is a ring linking three completely disjoint[lower-alpha 25] great squares.[lower-alpha 28]
Hypercubic chords

The 24 vertices of the 24-cell are distributed[12] at four different chord lengths from each other: √1, √2, √3 and √4.
Each vertex is joined to 8 others[lower-alpha 29] by an edge of length 1, spanning 60° = π/3 of arc. Next nearest are 6 vertices[lower-alpha 30] located 90° = π/2 away, along an interior chord of length √2. Another 8 vertices lie 120° = 2π/3 away, along an interior chord of length √3.[lower-alpha 31] The opposite vertex is 180° = π away along a diameter of length 2. Finally, as the 24-cell is radially equilateral, its center can be treated[lower-alpha 32] as a 25th canonical apex vertex,[lower-alpha 33] which is 1 edge length away from all the others.
To visualize how the interior polytopes of the 24-cell fit together (as described below), keep in mind that the four chord lengths (√1, √2, √3, √4) are the long diameters of the hypercubes of dimensions 1 through 4: the long diameter of the square is √2; the long diameter of the cube is √3; and the long diameter of the tesseract is √4.[lower-alpha 34] Moreover, the long diameter of the octahedron is √2 like the square; and the long diameter of the 24-cell itself is √4 like the tesseract. In the 24-cell, the √2 chords are the edges of central squares, and the √4 chords are the diagonals of central squares.
Geodesics

The vertex chords of the 24-cell are arranged in geodesic great circle polygons.[lower-alpha 36] The geodesic distance between two 24-cell vertices along a path of √1 edges is always 1, 2, or 3, and it is 3 only for opposite vertices.[lower-alpha 37]
The √1 edges occur in 16 hexagonal great circles (in planes inclined at 60 degrees to each other), 4 of which cross[lower-alpha 19] at each vertex.[lower-alpha 18] The 96 distinct √1 edges divide the surface into 96 triangular faces and 24 octahedral cells: a 24-cell. The 16 hexagonal great circles can be divided into 4 sets of 4 non-intersecting Clifford parallel geodesics, such that only one hexagonal great circle in each set passes through each vertex, and the 4 hexagons in each set reach all 24 vertices.[lower-alpha 40]
| Coxeter plane | F4 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | [12] | |
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph | 
|
|
| Dihedral symmetry | [6] | [6] |
| Coxeter plane | B4 | B2 / A3 |
| Graph | 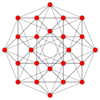
|

|
| Dihedral symmetry | [8] | [4] |
The √2 chords occur in 18 square great circles (3 sets of 6 orthogonal planes[lower-alpha 10]), 3 of which cross at each vertex.[lower-alpha 41] The 72 distinct √2 chords do not run in the same planes as the hexagonal great circles; they do not follow the 24-cell's edges, they pass through its octagonal cell centers.[lower-alpha 42] The 72 √2 chords are the 3 orthogonal axes of the 24 octahedral cells, joining vertices which are 2 √1 edges apart. The 18 square great circles can be divided into 3 sets of 6 non-intersecting Clifford parallel geodesics,[lower-alpha 35] such that only one square great circle in each set passes through each vertex, and the 6 squares in each set reach all 24 vertices.[lower-alpha 46]
The √3 chords occur in 32 triangular great circles in 16 planes, 4 of which cross at each vertex.[lower-alpha 31] The 96 distinct √3 chords[lower-alpha 23] run vertex-to-every-other-vertex in the same planes as the hexagonal great circles.[lower-alpha 24] They are the 3 edges of the 32 great triangles inscribed in the 16 great hexagons, joining vertices which are 2 √1 edges apart on a great circle.[lower-alpha 22]
The √4 chords occur as 12 vertex-to-vertex diameters (3 sets of 4 orthogonal axes), the 24 radii around the 25th central vertex.[lower-alpha 33]
The sum of the squared lengths[lower-alpha 47] of all these distinct chords of the 24-cell is 576 = 242.[lower-alpha 48] These are all the central polygons through vertices, but in 4-space there are geodesics on the 3-sphere which do not lie in central planes at all. There are geodesic shortest paths between two 24-cell vertices that are helical rather than simply circular; they corresponding to diagonal isoclinic rotations rather than simple rotations.[lower-alpha 49]
The √1 edges occur in 48 parallel pairs, √3 apart. The √2 chords occur in 36 parallel pairs, √2 apart. The √3 chords occur in 48 parallel pairs, √1 apart.[lower-alpha 50]
The central planes of the 24-cell can be divided into 4 orthogonal central hyperplanes (3-spaces) each forming a cuboctahedron. The great hexagons are 60 degrees apart; the great squares are 90 degrees or 60 degrees apart; a great square and a great hexagon are 90 degrees and 60 degrees apart.[lower-alpha 52] Each set of similar central polygons (squares or hexagons) can be divided into 4 sets of non-intersecting Clifford parallel polygons (of 6 squares or 4 hexagons).[lower-alpha 53] Each set of Clifford parallel great circles is a parallel fiber bundle which visits all 24 vertices just once.
Each great circle intersects[lower-alpha 11] with the other great circles to which it is not Clifford parallel at one √4 diameter of the 24-cell.[lower-alpha 54] Great circles which are completely orthogonal[lower-alpha 7] or otherwise Clifford parallel[lower-alpha 35] do not intersect at all: they pass through disjoint sets of vertices.[lower-alpha 55]
Constructions
Triangles and squares come together uniquely in the 24-cell to generate, as interior features,[lower-alpha 32] all of the triangle-faced and square-faced regular convex polytopes in the first four dimensions (with caveats for the 5-cell and the 600-cell).[lower-alpha 56] Consequently, there are numerous ways to construct or deconstruct the 24-cell.
Reciprocal constructions from 8-cell and 16-cell
The 8 integer vertices (±1, 0, 0, 0) are the vertices of a regular 16-cell, and the 16 half-integer vertices (±1/2, ±1/2, ±1/2, ±1/2) are the vertices of its dual, the tesseract (8-cell).[21] The tesseract gives Gosset's construction[22] of the 24-cell, equivalent to cutting a tesseract into 8 cubic pyramids, and then attaching them to the facets of a second tesseract. The analogous construction in 3-space gives the rhombic dodecahedron which, however, is not regular.[lower-alpha 57] The 16-cell gives the reciprocal construction of the 24-cell, Cesaro's construction,[23] equivalent to rectifying a 16-cell (truncating its corners at the mid-edges, as described above). The analogous construction in 3-space gives the cuboctahedron (dual of the rhombic dodecahedron) which, however, is not regular. The tesseract and the 16-cell are the only regular 4-polytopes in the 24-cell.[24]
We can further divide the 16 half-integer vertices into two groups: those whose coordinates contain an even number of minus (−) signs and those with an odd number. Each of these groups of 8 vertices also define a regular 16-cell. This shows that the vertices of the 24-cell can be grouped into three disjoint sets of eight with each set defining a regular 16-cell, and with the complement defining the dual tesseract.[25] This also shows that the symmetries of the 16-cell form a subgroup of index 3 of the symmetry group of the 24-cell.[lower-alpha 27]
Diminishings
We can facet the 24-cell by cutting[lower-alpha 58] through interior cells bounded by vertex chords to remove vertices, exposing the facets of interior 4-polytopes inscribed in the 24-cell. One can cut a 24-cell through any planar hexagon of 6 vertices, any planar rectangle of 4 vertices, or any triangle of 3 vertices. The great circle central planes (above) are only some of those planes. Here we shall expose some of the others: the face planes[lower-alpha 59] of interior polytopes.[lower-alpha 60]
8-cell
Starting with a complete 24-cell, remove 8 orthogonal vertices (4 opposite pairs on 4 perpendicular axes), and the 8 edges which radiate from each, by cutting through 8 cubic cells bounded by √1 edges to remove 8 cubic pyramids whose apexes are the vertices to be removed. This removes 4 edges from each hexagonal great circle (retaining just one opposite pair of edges), so no continuous hexagonal great circles remain. Now 3 perpendicular edges meet and form the corner of a cube at each of the 16 remaining vertices,[lower-alpha 61] and the 32 remaining edges divide the surface into 24 square faces and 8 cubic cells: a tesseract. There are three ways you can do this (choose a set of 8 orthogonal vertices out of 24), so there are three such tesseracts inscribed in the 24-cell.[lower-alpha 22] They overlap with each other, but most of their element sets are disjoint: they share some vertex count, but no edge length, face area, or cell volume.[lower-alpha 62] They do share 4-content, their common core.[lower-alpha 63]
16-cell
Starting with a complete 24-cell, remove the 16 vertices of a tesseract (retaining the 8 vertices you removed above), by cutting through 16 tetrahedral cells bounded by √2 chords to remove 16 tetrahedral pyramids whose apexes are the vertices to be removed. This removes 12 great squares (retaining just one orthogonal set) and all the √1 edges, exposing √2 chords as the new edges. Now the remaining 6 great squares cross perpendicularly, 3 at each of 8 remaining vertices,[lower-alpha 64] and their 24 edges divide the surface into 32 triangular faces and 16 tetrahedral cells: a 16-cell. There are three ways you can do this (remove 1 of 3 sets of tesseract vertices), so there are three such 16-cells inscribed in the 24-cell.[lower-alpha 26] They overlap with each other, but all of their element sets are disjoint:[lower-alpha 25] they do not share any vertex count, edge length,[lower-alpha 65] or face area, but they do share cell volume. They also share 4-content, their common core.[lower-alpha 63]
Tetrahedral constructions
The 24-cell can be constructed radially from 96 equilateral triangles of edge length √1 which meet at the center of the polytope, each contributing two radii and an edge.[lower-alpha 2] They form 96 √1 tetrahedra (each contributing one 24-cell face), all sharing the 25th central apex vertex. These form 24 octahedral pyramids (half-16-cells) with their apexes at the center.
The 24-cell can be constructed from 96 equilateral triangles of edge length √2, where the three vertices of each triangle are located 90° = π/2 away from each other on the 3-sphere. They form 48 √2 tetrahedra (the cells of the three 16-cells), centered at the 24 mid-edge-radii of the 24-cell.[lower-alpha 65]
The 24-cell can be constructed directly from its characteristic simplex ![]()
![]()
![]()
![]()
![]()
![]()
![]() , the irregular 5-cell which is the fundamental region of its symmetry group F4, by reflection of that 4-orthoscheme in its own cells (which are 3-orthoschemes).[lower-alpha 66]
, the irregular 5-cell which is the fundamental region of its symmetry group F4, by reflection of that 4-orthoscheme in its own cells (which are 3-orthoschemes).[lower-alpha 66]
Relationships among interior polytopes
The 24-cell, three tesseracts, and three 16-cells are deeply entwined around their common center, and intersect in a common core.[lower-alpha 63] The tesseracts and the 16-cells are rotated 60° isoclinically[lower-alpha 15] with respect to each other. This means that the corresponding vertices of two tesseracts or two 16-cells are √3 (120°) apart.[lower-alpha 22]
The tesseracts are inscribed in the 24-cell[lower-alpha 67] such that their vertices and edges are exterior elements of the 24-cell, but their square faces and cubical cells lie inside the 24-cell (they are not elements of the 24-cell). The 16-cells are inscribed in the 24-cell[lower-alpha 68] such that only their vertices are exterior elements of the 24-cell: their edges, triangular faces, and tetrahedral cells lie inside the 24-cell. The interior[lower-alpha 69] 16-cell edges have length √2.[lower-alpha 28]
The 16-cells are also inscribed in the tesseracts: their √2 edges are the face diagonals of the tesseract, and their 8 vertices occupy every other vertex of the tesseract. Each tesseract has two 16-cells inscribed in it (occupying the opposite vertices and face diagonals), so each 16-cell is inscribed in two of the three 8-cells.[29][lower-alpha 27] This is reminiscent of the way, in 3 dimensions, two opposing regular tetrahedra can be inscribed in a cube, as discovered by Kepler.[28] In fact it is the exact dimensional analogy (the demihypercubes), and the 48 tetrahedral cells are inscribed in the 24 cubical cells in just that way.[30][lower-alpha 65]
The 24-cell encloses the three tesseracts within its envelope of octahedral facets, leaving 4-dimensional space in some places between its envelope and each tesseract's envelope of cubes. Each tesseract encloses two of the three 16-cells, leaving 4-dimensional space in some places between its envelope and each 16-cell's envelope of tetrahedra. Thus there are measurable[7] 4-dimensional interstices[lower-alpha 70] between the 24-cell, 8-cell and 16-cell envelopes. The shapes filling these gaps are 4-pyramids, alluded to above.[lower-alpha 71]
Boundary cells
Despite the 4-dimensional interstices between 24-cell, 8-cell and 16-cell envelopes, their 3-dimensional volumes overlap. The different envelopes are separated in some places, and in contact in other places (where no 4-pyramid lies between them). Where they are in contact, they merge and share cell volume: they are the same 3-membrane in those places, not two separate but adjacent 3-dimensional layers.[lower-alpha 73] Because there are a total of 7 envelopes, there are places where several envelopes come together and merge volume, and also places where envelopes interpenetrate (cross from inside to outside each other).
Some interior features lie within the 3-space of the (outer) boundary envelope of the 24-cell itself: each octahedral cell is bisected by three perpendicular squares (one from each of the tesseracts), and the diagonals of those squares (which cross each other perpendicularly at the center of the octahedron) are 16-cell edges (one from each 16-cell). Each square bisects an octahedron into two square pyramids, and also bonds two adjacent cubic cells of a tesseract together as their common face.[lower-alpha 72]
As we saw above, 16-cell √2 tetrahedral cells are inscribed in tesseract √1 cubic cells, sharing the same volume. 24-cell √1 octahedral cells overlap their volume with √1 cubic cells: they are bisected by a square face into two square pyramids,[32] the apexes of which also lie at a vertex of a cube.[lower-alpha 74] The octahedra share volume not only with the cubes, but with the tetrahedra inscribed in them; thus the 24-cell, tesseracts, and 16-cells all share some boundary volume.[lower-alpha 73]
As a configuration
This configuration matrix[33] represents the 24-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 24-cell. The non-diagonal numbers say how many of the column's element occur in or at the row's element.
[math]\displaystyle{ \begin{bmatrix}\begin{matrix}24 & 8 & 12 & 6 \\ 2 & 96 & 3 & 3 \\ 3 & 3 & 96 & 2 \\ 6 & 12 & 8 & 24 \end{matrix}\end{bmatrix} }[/math]
Since the 24-cell is self-dual, its matrix is identical to its 180 degree rotation.
Symmetries, root systems, and tessellations

The 24 root vectors of the D4 root system of the simple Lie group SO(8) form the vertices of a 24-cell. The vertices can be seen in 3 hyperplanes,[lower-alpha 51] with the 6 vertices of an octahedron cell on each of the outer hyperplanes and 12 vertices of a cuboctahedron on a central hyperplane. These vertices, combined with the 8 vertices of the 16-cell, represent the 32 root vectors of the B4 and C4 simple Lie groups.
The 48 vertices (or strictly speaking their radius vectors) of the union of the 24-cell and its dual form the root system of type F4.[35] The 24 vertices of the original 24-cell form a root system of type D4; its size has the ratio √2:1. This is likewise true for the 24 vertices of its dual. The full symmetry group of the 24-cell is the Weyl group of F4, which is generated by reflections through the hyperplanes orthogonal to the F4 roots. This is a solvable group of order 1152. The rotational symmetry group of the 24-cell is of order 576.
Quaternionic interpretation

When interpreted as the quaternions,[lower-alpha 13] the F4 root lattice (which is the integral span of the vertices of the 24-cell) is closed under multiplication and is therefore a ring. This is the ring of Hurwitz integral quaternions. The vertices of the 24-cell form the group of units (i.e. the group of invertible elements) in the Hurwitz quaternion ring (this group is also known as the binary tetrahedral group). The vertices of the 24-cell are precisely the 24 Hurwitz quaternions with norm squared 1, and the vertices of the dual 24-cell are those with norm squared 2. The D4 root lattice is the dual of the F4 and is given by the subring of Hurwitz quaternions with even norm squared.[37]
Viewed as the 24 unit Hurwitz quaternions, the unit radius coordinates of the 24-cell represent (in antipodal pairs) the 12 rotations of a regular tetrahedron.[38]
Vertices of other convex regular 4-polytopes also form multiplicative groups of quaternions, but few of them generate a root lattice.
Voronoi cells
The Voronoi cells of the D4 root lattice are regular 24-cells. The corresponding Voronoi tessellation gives the tessellation of 4-dimensional Euclidean space by regular 24-cells, the 24-cell honeycomb. The 24-cells are centered at the D4 lattice points (Hurwitz quaternions with even norm squared) while the vertices are at the F4 lattice points with odd norm squared. Each 24-cell of this tessellation has 24 neighbors. With each of these it shares an octahedron. It also has 24 other neighbors with which it shares only a single vertex. Eight 24-cells meet at any given vertex in this tessellation. The Schläfli symbol for this tessellation is {3,4,3,3}. It is one of only three regular tessellations of R4.
The unit balls inscribed in the 24-cells of this tessellation give rise to the densest known lattice packing of hyperspheres in 4 dimensions. The vertex configuration of the 24-cell has also been shown to give the highest possible kissing number in 4 dimensions.
Radially equilateral honeycomb
The dual tessellation of the 24-cell honeycomb {3,4,3,3} is the 16-cell honeycomb {3,3,4,3}. The third regular tessellation of four dimensional space is the tesseractic honeycomb {4,3,3,4}, whose vertices can be described by 4-integer Cartesian coordinates.[lower-alpha 13] The congruent relationships among these three tessellations can be helpful in visualizing the 24-cell, in particular the radial equilateral symmetry which it shares with the tesseract.[lower-alpha 2]
A honeycomb of unit edge length 24-cells may be overlaid on a honeycomb of unit edge length tesseracts such that every vertex of a tesseract (every 4-integer coordinate) is also the vertex of a 24-cell (and tesseract edges are also 24-cell edges), and every center of a 24-cell is also the center of a tesseract.[39] The 24-cells are twice as large as the tesseracts by 4-dimensional content (hypervolume), so overall there are two tesseracts for every 24-cell, only half of which are inscribed in a 24-cell. If those tesseracts are colored black, and their adjacent tesseracts (with which they share a cubical facet) are colored red, a 4-dimensional checkerboard results.[40] Of the 24 center-to-vertex radii[lower-alpha 75] of each 24-cell, 16 are also the radii of a black tesseract inscribed in the 24-cell. The other 8 radii extend outside the black tesseract (through the centers of its cubical facets) to the centers of the 8 adjacent red tesseracts. Thus the 24-cell honeycomb and the tesseractic honeycomb coincide in a special way: 8 of the 24 vertices of each 24-cell do not occur at a vertex of a tesseract (they occur at the center of a tesseract instead). Each black tesseract is cut from a 24-cell by truncating it at these 8 vertices, slicing off 8 cubic pyramids (as in reversing Gosset's construction,[22] but instead of being removed the pyramids are simply colored red and left in place). Eight 24-cells meet at the center of each red tesseract: each one meets its opposite at that shared vertex, and the six others at a shared octahedral cell.
The red tesseracts are filled cells (they contain a central vertex and radii); the black tesseracts are empty cells. The vertex set of this union of two honeycombs includes the vertices of all the 24-cells and tesseracts, plus the centers of the red tesseracts. Adding the 24-cell centers (which are also the black tesseract centers) to this honeycomb yields a 16-cell honeycomb, the vertex set of which includes all the vertices and centers of all the 24-cells and tesseracts. The formerly empty centers of adjacent 24-cells become the opposite vertices of a unit edge length 16-cell. 24 half-16-cells (octahedral pyramids) meet at each formerly empty center to fill each 24-cell, and their octahedral bases are the 6-vertex octahedral facets of the 24-cell (shared with an adjacent 24-cell).[lower-alpha 76]
Notice the complete absence of pentagons anywhere in this union of three honeycombs. Like the 24-cell, 4-dimensional Euclidean space itself is entirely filled by a complex of all the polytopes that can be built out of regular triangles and squares (except the 5-cell), but that complex does not require (or permit) any of the pentagonal polytopes.[lower-alpha 3]
Rotations
The regular convex 4-polytopes are an expression of their underlying symmetry which is known as SO(4), the group of rotations[41] about a fixed point in 4-dimensional Euclidean space.[lower-alpha 79]
The 3 Cartesian bases of the 24-cell
There are three distinct orientations of the tesseractic honeycomb which could be made to coincide with the 24-cell honeycomb, depending on which of the 24-cell's three disjoint sets of 8 orthogonal vertices (which set of 4 perpendicular axes, or equivalently, which inscribed basis 16-cell)[lower-alpha 16] was chosen to align it, just as three tesseracts can be inscribed in the 24-cell, rotated with respect to each other.[lower-alpha 22] The distance from one of these orientations to another is an isoclinic rotation through 60 degrees (a double rotation of 60 degrees in each pair of orthogonal invariant planes, around a single fixed point).[lower-alpha 80] This rotation can be seen most clearly in the hexagonal central planes, where every hexagon rotates to change which of its three diameters is aligned with a coordinate system axis.[lower-alpha 17]
Planes of rotation
Rotations in 4-dimensional Euclidean space can be seen as the composition of two 2-dimensional rotations in completely orthogonal planes.[43] Thus the general rotation in 4-space is a double rotation.[44] There are two important special cases, called a simple rotation and an isoclinic rotation.[lower-alpha 84]
Simple rotations

In 3 dimensions a spinning polyhedron has a single invariant central plane of rotation. The plane is called invariant because each point in the plane moves in a circle but stays within the plane. Only one of a polyhedron's central planes can be invariant during a particular rotation; the choice of invariant central plane, and the angular distance and direction it is rotated, completely specifies the rotation. Points outside the invariant plane also move in circles (unless they are on the fixed axis of rotation perpendicular to the invariant plane), but the circles do not lie within a central plane.
When a 4-polytope is rotating with only one invariant central plane, the same kind of simple rotation is happening that occurs in 3 dimensions. One difference is that instead of a fixed axis of rotation, there is an entire fixed central plane in which the points do not move. The fixed plane is the one central plane that is completely orthogonal[lower-alpha 7] to the invariant plane of rotation. In the 24-cell, there is a simple rotation which will take any vertex directly to any other vertex, also moving most of the other vertices but leaving at least 2 and at most 6 other vertices fixed (the vertices that the fixed central plane intersects). The vertex moves along a great circle in the invariant plane of rotation between adjacent vertices of a great hexagon, a great square or a great digon, and the completely orthogonal fixed plane is a digon, a square or a hexagon, respectively. [lower-alpha 55]
Double rotations
The points in the completely orthogonal central plane are not constrained to be fixed. It is also possible for them to be rotating in circles, as a second invariant plane, at a rate independent of the first invariant plane's rotation: a double rotation in two perpendicular non-intersecting planes[lower-alpha 9] of rotation at once.[lower-alpha 83] In a double rotation there is no fixed plane or axis: every point moves except the center point. The angular distance rotated may be different in the two completely orthogonal central planes, but they are always both invariant: their circularly moving points remain within the plane as the whole plane tilts sideways in the completely orthogonal rotation. A rotation in 4-space always has (at least) two completely orthogonal invariant planes of rotation, although in a simple rotation the angle of rotation in one of them is 0.
Double rotations come in two chiral forms: left and right rotations.[lower-alpha 85] In a double rotation each vertex moves in a spiral along two orthogonal great circles at once.[lower-alpha 81] Either the path is right-hand threaded (like most screws and bolts), moving along the circles in the "same" directions, or it is left-hand threaded (like a reverse-threaded bolt), moving along the circles in what we conventionally say are "opposite" directions (according to the right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes).[46]
In double rotations of the 24-cell that take vertices to vertices, one invariant plane of rotation contains either a great hexagon, a great square, or only an axis (two vertices, a great digon). The completely orthogonal invariant plane of rotation will necessarily contain a great digon, a great square, or a great hexagon, respectively. The selection of an invariant plane of rotation, a rotational direction and angle through which to rotate it, and a rotational direction and angle through which to rotate its completely orthogonal plane, completely determines the nature of the rotational displacement. In the 24-cell there are several noteworthy kinds of double rotation permitted by these parameters.[47]
Isoclinic rotations
When the angles of rotation in the two invariant planes are exactly the same, a remarkably symmetric transformation occurs:[48] all the great circle planes Clifford parallel[lower-alpha 35] to the invariant planes become invariant planes of rotation themselves, through that same angle, and the 4-polytope rotates isoclinically in many directions at once.[49] Each vertex moves an equal distance in four orthogonal directions at the same time.[lower-alpha 15] In the 24-cell any isoclinic rotation through 60 degrees in a hexagonal plane takes each vertex to a vertex two edge lengths away, rotates all 16 hexagons by 60 degrees, and takes every great circle polygon (square,[lower-alpha 43] hexagon or triangle) to a Clifford parallel great circle polygon of the same kind 120 degrees away. An isoclinic rotation is also called a Clifford displacement, after its discoverer.[lower-alpha 80]
The 24-cell in the double rotation animation appears to turn itself inside out.[lower-alpha 88] It appears to, because it actually does, reversing the chirality of the whole 4-polytope just the way your bathroom mirror reverses the chirality of your image by a 180 degree reflection. Each 360 degree isoclinic rotation is as if the 24-cell surface had been stripped off like a glove and turned inside out, making a right-hand glove into a left-hand glove (or vice versa).[50]
In a simple rotation of the 24-cell in a hexagonal plane, each vertex in the plane rotates first along an edge to an adjacent vertex 60 degrees away. But in an isoclinic rotation in two completely orthogonal planes one of which is a great hexagon,[lower-alpha 55] each vertex rotates first to a vertex two edge lengths away (√3 and 120° distant). The double 60-degree rotation's helical geodesics pass through every other vertex, missing the vertices in between.[lower-alpha 21] Each √3 chord of the helical geodesic[lower-alpha 94] crosses between two Clifford parallel hexagon central planes, and lies in another hexagon central plane that intersects them both.[lower-alpha 99] The √3 chords meet at a 60° angle, but since they lie in different planes they form a helix not a triangle. Three √3 chords and 360° of rotation takes the vertex to an adjacent vertex, not back to itself. The helix of √3 chords closes into a loop only after six √3 chords: a 720° rotation twice around the 24-cell[lower-alpha 82] on a skew hexagram with √3 edges.[lower-alpha 98] Even though all 24 vertices and all the hexagons rotate at once, a 360 degree isoclinic rotation moves each vertex only half way around its circuit. After 360 degrees each helix has departed from 3 vertices and reached a fourth vertex adjacent to the original vertex, but has not arrived back exactly at the vertex it departed from. Each central plane (every hexagon or square in the 24-cell) has rotated 360 degrees and been tilted sideways all the way around 360 degrees back to its original position (like a coin flipping twice), but the 24-cell's orientation in the 4-space in which it is embedded is now different.[52] Because the 24-cell is now inside-out, if the isoclinic rotation is continued in the same direction through another 360 degrees, the 24 moving vertices will pass through the other half of the vertices that were missed on the first revolution (the 12 antipodal vertices of the 12 that were hit the first time around), and each isoclinic geodesic will arrive back at the vertex it departed from, forming a closed six-chord helical loop. It takes a 720 degree isoclinic rotation for each hexagram2 geodesic to complete a circuit through every second vertex of its six vertices by winding around the 24-cell twice, returning the 24-cell to its original chiral orientation.[lower-alpha 106]
The hexagonal winding path that each vertex takes as it loops twice around the 24-cell forms a double helix bent into a Möbius ring, so that the two strands of the double helix form a continuous single strand in a closed loop.[lower-alpha 101] In the first revolution the vertex traverses one 3-chord strand of the double helix; in the second revolution it traverses the second 3-chord strand, moving in the same rotational direction with the same handedness (bending either left or right) throughout. Although this isoclinic Möbius ring is a closed spiral not a 2-dimensional circle, like a great circle it is a geodesic because it is the shortest path from vertex to vertex.[lower-alpha 49]
Clifford parallel polytopes
Two planes are also called isoclinic if an isoclinic rotation will bring them together.[lower-alpha 52] The isoclinic planes are precisely those central planes with Clifford parallel geodesic great circles.[54] Clifford parallel great circles do not intersect,[lower-alpha 35] so isoclinic great circle polygons have disjoint vertices. In the 24-cell every hexagonal central plane is isoclinic to three others, and every square central plane is isoclinic to five others. We can pick out 4 mutually isoclinic (Clifford parallel) great hexagons (four different ways) covering all 24 vertices of the 24-cell just once (a hexagonal fibration).[lower-alpha 40] We can pick out 6 mutually isoclinic (Clifford parallel) great squares[lower-alpha 90] (three different ways) covering all 24 vertices of the 24-cell just once (a square fibration).[lower-alpha 46] Every isoclinic rotation taking vertices to vertices corresponds to a discrete fibration.[lower-alpha 110]
Two dimensional great circle polygons are not the only polytopes in the 24-cell which are parallel in the Clifford sense.[56] Congruent polytopes of 2, 3 or 4 dimensions can be said to be Clifford parallel in 4 dimensions if their corresponding vertices are all the same distance apart. The three 16-cells inscribed in the 24-cell are Clifford parallels. Clifford parallel polytopes are completely disjoint polytopes.[lower-alpha 25] A 60 degree isoclinic rotation in hexagonal planes takes each 16-cell to a disjoint 16-cell. Like all double rotations, isoclinic rotations come in two chiral forms: there is a disjoint 16-cell to the left of each 16-cell, and another to its right.[lower-alpha 26]
All Clifford parallel 4-polytopes are related by an isoclinic rotation,[lower-alpha 80] but not all isoclinic polytopes are Clifford parallels (completely disjoint).[lower-alpha 111] The three 8-cells in the 24-cell are isoclinic but not Clifford parallel. Like the 16-cells, they are rotated 60 degrees isoclinically with respect to each other, but their vertices are not all disjoint (and therefore not all equidistant). Each vertex occurs in two of the three 8-cells (as each 16-cell occurs in two of the three 8-cells).[lower-alpha 22]
Isoclinic rotations relate the convex regular 4-polytopes to each other. An isoclinic rotation of a single 16-cell will generate[lower-alpha 112] a 24-cell. A simple rotation of a single 16-cell will not, because its vertices will not reach either of the other two 16-cells' vertices in the course of the rotation. An isoclinic rotation of the 24-cell will generate the 600-cell, and an isoclinic rotation of the 600-cell will generate the 120-cell. (Or they can all be generated directly by an isoclinic rotation of the 16-cell, generating isoclinic copies of itself.) The convex regular 4-polytopes nest inside each other, and hide next to each other in the Clifford parallel spaces that comprise the 3-sphere.[57] For an object of more than one dimension, the only way to reach these parallel subspaces directly is by isoclinic rotation.[lower-alpha 113]
Rings
In the 24-cell there are sets of rings of six different kinds, described separately in detail in other sections of this article. This section describes how the different kinds of rings are intertwined.
The 24-cell contains four kinds of geodesic fibers (polygonal rings running through vertices): great circle squares and their isoclinic helix octagrams,[lower-alpha 46] and great circle hexagons and their isoclinic helix hexagrams.[lower-alpha 40] It also contains two kinds of cell rings (chains of octahedra bent into a ring in the fourth dimension): four octahedra connected vertex-to-vertex and bent into a square, and six octahedra connected face-to-face and bent into a hexagon.
4-cell rings
Four unit-edge-length octahedra can be connected vertex-to-vertex along a common axis of length 4√2. The axis can then be bent into a square of edge length √2. Although it is possible to do this in a space of only three dimensions, that is not how it occurs in the 24-cell. Although the √2 axes of the four octahedra occupy the same plane, forming one of the 18 √2 great squares of the 24-cell, each octahedron occupies a different 3-dimensional hyperplane,[lower-alpha 114] and all four dimensions are utilized. The 24-cell can be partitioned into 6 such 4-cell rings (three different ways), mutually interlinked like adjacent links in a chain (but these links all have a common center). An isoclinic rotation in the great square plane by a multiple of 90° takes each octahedron in the ring to an octahedron in the ring.
6-cell rings

Six regular octahedra can be connected face-to-face along a common axis that passes through their centers of volume, forming a stack or column with only triangular faces. In a space of four dimensions, the axis can then be bent 60° in the fourth dimension at each of the six octahedron centers, in a plane orthogonal to all three orthogonal central planes of each octahedron, such that the top and bottom triangular faces of the column become coincident. The column becomes a ring around a hexagonal axis. The 24-cell can be partitioned into 4 such rings (four different ways), mutually interlinked. Because the hexagonal axis joins cell centers (not vertices), it is not a great hexagon of the 24-cell.[lower-alpha 117] However, six great hexagons can be found in the ring of six octahedra, running along the edges of the octahedra. In the column of six octahedra (before it is bent into a ring) there are six spiral paths along edges running up the column: three parallel helices spiraling clockwise, and three parallel helices spiraling counterclockwise. Each clockwise helix intersects each counterclockwise helix at two vertices three edge lengths apart. Bending the column into a ring changes these helices into great circle hexagons.[lower-alpha 115] The ring has two sets of three great hexagons, each on three Clifford parallel great circles.[lower-alpha 119] The great hexagons in each parallel set of three do not intersect, but each intersects the other three great hexagons (to which it is not Clifford parallel) at two antipodal vertices.
A simple rotation in any of the great hexagon planes by a multiple of 60° rotates only that hexagon invariantly, taking each vertex in that hexagon to a vertex in the same hexagon. An isoclinic rotation by 60° in any of the six great hexagon planes rotates all three Clifford parallel great hexagons invariantly, and takes each octahedron in the ring to a non-adjacent octahedron in the ring.[lower-alpha 121]
Each isoclinically displaced octahedron is also rotated itself. After a 360° isoclinic rotation each octahedron is back in the same position, but in a different orientation. In a 720° isoclinic rotation, its vertices are returned to their original orientation.
Four great hexagons comprise a discrete fiber bundle covering all 24 vertices in a Hopf fibration. Four 6-cell rings comprise the same discrete fibration. The 24-cell has four such discrete hexagonal fibrations, and each is the domain (container) of a unique left-right pair of isoclinic rotations (left and right Hopf fiber bundles). Each great hexagon belongs to just one fibration,[59] but each 6-cell ring belongs to three fibrations. The 24-cell contains 16 great hexagons, divided among four fibrations, each of which is a set of four 6-cell rings, but the 24-cell has only four distinct 6-cell rings. Each 6-cell ring contains 3 of the great hexagons in each of three fibrations: only 3 of the 4 Clifford parallel hexagons of each of the three fibrations, and only 18 of the 24 vertices.[lower-alpha 110]
Helical hexagrams and their 4𝝅 isoclines
Another kind of geodesic fiber, the helical hexagram isoclines, can be found within a 6-cell ring of octahedra. Each of these geodesics runs through every second vertex of a skew hexagram2, which in the unit-radius, unit-edge-length 24-cell has six √3 edges. The hexagram does not lie in a single central plane, but is composed of six linked √3 chords from the six different hexagon great circles in the 6-cell ring. The isocline geodesic fiber is the path of an isoclinic rotation,[lower-alpha 49] a helical rather than simply circular path around the 24-cell which links vertices two edge lengths apart and consequently must wrap twice around the 24-cell before completing its six-vertex loop.[lower-alpha 87] Rather than a flat hexagon, it forms a skew hexagram out of two three-sided 360 degree half-loops: open triangles joined end-to-end to each other in a six-sided Möbius loop.[lower-alpha 101]
Each 6-cell ring contains six such hexagram isoclines, three black and three white, that connect even and odd vertices respectively.[lower-alpha 118] Each of the three black-white pairs of isoclines belongs to one of the three fibrations in which the 6-cell ring occurs. Each fibration's right (or left) rotation traverses two black isoclines and two white isoclines in parallel, rotating all 24 vertices.[lower-alpha 21]
Beginning at any vertex at one end of the column of six octahedra, we can follow an isoclinic path of √3 chords of an isocline from octahedron to octahedron. In the 24-cell the √1 edges are great hexagon edges (and octahedron edges); in the column of six octahedra we see six great hexagons running along the octahedra's edges. The √3 chords are great hexagon diagonals, joining great hexagon vertices two √1 edges apart. We find them in the ring of six octahedra running from a vertex in one octahedron to a vertex in the next octahedron, passing through the face shared by the two octahedra (but not touching any of the face's 3 vertices). Each √3 chord is a chord of just one great hexagon (an edge of a great triangle inscribed in that great hexagon), but successive √3 chords belong to different great hexagons.[lower-alpha 99] At each vertex the isoclinic path of √3 chords bends 60 degrees in two central planes[lower-alpha 122] at once: 60 degrees around the great hexagon that the chord before the vertex belongs to, and 60 degrees into the plane of a different great hexagon entirely, that the chord after the vertex belongs to.[lower-alpha 125] Thus the path follows one great hexagon from each octahedron to the next, but switches to another of the six great hexagons in the next link of the hexagram2 path. Followed along the column of six octahedra (and "around the end" where the column is bent into a ring) the path may at first appear to be zig-zagging between three adjacent parallel hexagonal central planes (like a Petrie polygon), but it is not: any isoclinic path we can pick out always zig-zags between two sets of three adjacent parallel hexagonal central planes, intersecting only every even (or odd) vertex and never changing its inherent even/odd parity, as it visits all six of the great hexagons in the 6-cell ring in rotation.[lower-alpha 86] When it has traversed one chord from each of the six great hexagons, after 720 degrees of isoclinic rotation (either left or right), it closes its skew hexagram and begins to repeat itself, circling again through the black (or white) vertices and cells.
At each vertex, there are four great hexagons[lower-alpha 127] and four hexagram isoclines (all black or all white) that cross at the vertex.[lower-alpha 128] Four hexagram isoclines (two black and two white) comprise a unique (left or right) fiber bundle of isoclines covering all 24 vertices in each distinct (left or right) isoclinic rotation. Each fibration has a unique left and right isoclinic rotation, and corresponding unique left and right fiber bundles of isoclines.[lower-alpha 129] There are 16 distinct hexagram isoclines in the 24-cell (8 black and 8 white).[lower-alpha 130] Each isocline is a skew Clifford polygon of no inherent chirality, but acts as a left (or right) isocline when traversed by a left (or right) rotation in different fibrations.[lower-alpha 87]
Helical octagrams and their 8𝝅 isoclines
The 24-cell contains 18 helical octagram isoclines, 9 left-handed and 9 right-handed. Three left-right pairs of octagram edge-helices are found in each of the three inscribed 16-cells, described elsewhere as the helical construction of the 16-cell. In summary, each 16-cell can be decomposed (three different ways) into a left-right pair of 8-cell rings of √2-edged tetrahedral cells. Each 8-cell ring twists either left or right around an axial octagram helix of eight chords. In each 16-cell there are exactly 6 distinct helices, identical octagrams which each circle through all eight vertices. Each acts as either a left helix or a right helix or a Petrie polygon in each of the six distinct isoclinic rotations (three left and three right), and has no inherent chirality except in respect to a particular rotation. The chords of these isoclines connect opposite vertices of face-bonded tetrahedral cells, which are also opposite vertices (antipodal vertices) of the 16-cell, so they are √4 chords.
In the 24-cell, these 18 helical octagram isoclines can be found within the six orthogonal 4-cell rings of octahedra. Each 4-cell ring has cells bonded vertex-to-vertex around a great square axis, and we find antipodal vertices at opposite vertices of the great square. A √4 chord (the diagonal of the great square) connects them; this is a chord of each distinct square isoclinic rotation. Boundary cells describes how the √2 axes of the 24-cell's octahedral cells are the edges of the 16-cell's tetrahedral cells, each tetrahedron is inscribed in a (tesseract) cube, and each octahedron is inscribed in a pair of cubes (from different tesseracts), bridging them.[lower-alpha 72] The vertex-bonded octahedra of the 4-cell ring also lie in different tesseracts.[lower-alpha 62] In the 24-cell, the 16-cells' isocline chords describe an octagram12{2} with √4 edges that run from the vertex of one cube and octahedron and tetrahedron, to the vertex of another cube and octahedron and tetrahedron (in a different tesseract), straight through the center of the 24-cell on one of the 12 √4 axes.
The octahedra in the 4-cell rings are vertex-bonded to more than two other octahedra, because three 4-cell rings (and their three axial great squares, which belong to different 16-cells) cross at 90° at each bonding vertex. At that vertex the octagram makes two right-angled turns at once: 90° around the great square, and 90° orthogonally into a different 4-cell ring entirely. The 180° arc of each √4 chord of the octagram runs through the volumes and opposite vertices of two face-bonded √2 tetrahedra (in the same 16-cell), which are also the opposite vertices of two vertex-bonded octahedra in different 4-cell rings (and different tesseracts). The arc does not hit any vertices of those two octahedra except the chord endpoints; in particular, it misses the vertex near the chord midpoint where the two octahedra are vertex-bonded. The 720° octagram isocline runs through one vertex of one octahedron in six different 4-cell rings (of the 18 4-cell rings in the 24-cell), and through the volumes of 16 tetrahedra. At each vertex, there are three great squares and six octagram isoclines (three left-right pairs) that cross at the vertex.[lower-alpha 90]
Each of the 3 fibrations of the 24-cell's 18 great squares corresponds to a distinct left (and right) isoclinic rotation in great square invariant planes. Each 60° step of the rotation takes 6 disjoint great squares (2 from each 16-cell) to great squares in a neighboring 16-cell, on 8-chord helical isoclines characteristic of the 16-cell.[lower-alpha 131]
This is the characteristic rotation of the 16-cell, not the 24-cell's characteristic rotation, and it does not take whole 16-cells of the 24-cell to each other the way the 24-cell's rotation in great hexagon planes does.[lower-alpha 132]
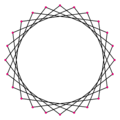
| Five ways of looking at a skew 24-gram | ||||
|---|---|---|---|---|
| Edge path | Petrie polygons | In a 600-cell | Discrete fibration | Isocline chords |
| 16-cells3{3/8} | Dodecagons2{12} | 24-gram{24/5} | Squares6{4} | {24/12}={12/2} |

|

|
|

|

|
| The 24-cell's three inscribed Clifford parallel 16-cells revealed as disjoint 8-point 4-polytopes with √2 edges. | 2 skew polygons of 12 √1 edges each. The 24-cell can be decomposed into 2 disjoint zig-zag dodecagons (4 different ways).[63] | In compounds of 5 24-cells, isoclines with golden chords of length φ = √2.𝚽 connect all 24-cells in 24-chord circuits.[64] | Their isoclinic rotation takes 6 Clifford parallel (disjoint) great squares with √2 edges to each other. | Adjacent vertices on an isocline are antipodal vertices of the 24-cell. The isocline chord is the √4 axis diameter.[lower-alpha 131] |
Characteristic orthoscheme
| Characteristics of the 24-cell[65] | |||||
|---|---|---|---|---|---|
| edge[66] | arc | dihedral[67] | |||
| 𝒍 | [math]\displaystyle{ 1 }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] | 120° | [math]\displaystyle{ \tfrac{2\pi}{3} }[/math] |
| 𝟀 | [math]\displaystyle{ \sqrt{\tfrac{1}{3}} \approx 0.577 }[/math] | 45° | [math]\displaystyle{ \tfrac{\pi}{4} }[/math] | 45° | [math]\displaystyle{ \tfrac{\pi}{4} }[/math] |
| 𝝉[lower-alpha 133] | [math]\displaystyle{ \sqrt{\tfrac{1}{4}} = 0.5 }[/math] | 30° | [math]\displaystyle{ \tfrac{\pi}{6} }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] |
| 𝟁 | [math]\displaystyle{ \sqrt{\tfrac{1}{12}} \approx 0.289 }[/math] | 30° | [math]\displaystyle{ \tfrac{\pi}{6} }[/math] | 60° | [math]\displaystyle{ \tfrac{\pi}{3} }[/math] |
| [math]\displaystyle{ _0R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{2}} \approx 0.707 }[/math] | 45° | [math]\displaystyle{ \tfrac{\pi}{4} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _1R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{4}} = 0.5 }[/math] | 30° | [math]\displaystyle{ \tfrac{\pi}{6} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _2R^3/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{6}} \approx 0.408 }[/math] | 30° | [math]\displaystyle{ \tfrac{\pi}{6} }[/math] | 90° | [math]\displaystyle{ \tfrac{\pi}{2} }[/math] |
| [math]\displaystyle{ _0R^4/l }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ _1R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{3}{4}} \approx 0.866 }[/math] | ||||
| [math]\displaystyle{ _2R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{2}{3}} \approx 0.816 }[/math] | ||||
| [math]\displaystyle{ _3R^4/l }[/math] | [math]\displaystyle{ \sqrt{\tfrac{1}{2}} \approx 0.707 }[/math] | ||||
Every regular 4-polytope has its characteristic 4-orthoscheme, an irregular 5-cell.[lower-alpha 66] The characteristic 5-cell of the regular 24-cell is represented by the Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , which can be read as a list of the dihedral angles between its mirror facets.[lower-alpha 134] It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular octahedron. The regular 24-cell is subdivided by its symmetry hyperplanes into 1152 instances of its characteristic 5-cell that all meet at its center.[69]
, which can be read as a list of the dihedral angles between its mirror facets.[lower-alpha 134] It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular octahedron. The regular 24-cell is subdivided by its symmetry hyperplanes into 1152 instances of its characteristic 5-cell that all meet at its center.[69]
The characteristic 5-cell (4-orthoscheme) has four more edges than its base characteristic tetrahedron (3-orthoscheme), joining the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 24-cell[lower-alpha 33]).[lower-alpha 135] If the regular 24-cell has radius and edge length 𝒍 = 1, its characteristic 5-cell's ten edges have lengths [math]\displaystyle{ \sqrt{\tfrac{1}{3}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{12}} }[/math] around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁),[lower-alpha 133] plus [math]\displaystyle{ \sqrt{\tfrac{1}{2}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{6}} }[/math] (the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the characteristic radii of the octahedron), plus [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ \sqrt{\tfrac{3}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{2}{3}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{2}} }[/math] (edges which are the characteristic radii of the 24-cell). The 4-edge path along orthogonal edges of the orthoscheme is [math]\displaystyle{ \sqrt{\tfrac{1}{4}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{12}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{6}} }[/math], [math]\displaystyle{ \sqrt{\tfrac{1}{2}} }[/math], first from a 24-cell vertex to a 24-cell edge center, then turning 90° to a 24-cell face center, then turning 90° to a 24-cell octahedral cell center, then turning 90° to the 24-cell center.
Reflections
The 24-cell can be constructed by the reflections of its characteristic 5-cell in its own facets (its tetrahedral mirror walls).[lower-alpha 136] Reflections and rotations are related: a reflection in an even number of intersecting mirrors is a rotation.[70] Consequently, regular polytopes can be generated by reflections or by rotations. For example, any 720° isoclinic rotation of the 24-cell in a hexagonal invariant plane takes each of the 24 vertices to and through 5 other vertices and back to itself, on a skew hexagram2 geodesic isocline that winds twice around the 3-sphere on every second vertex of the hexagram. Any set of four orthogonal pairs of antipodal vertices (the 8 vertices of one of the three inscribed 16-cells) performing half such an orbit visits 3 * 8 = 24 distinct vertices and generates the 24-cell sequentially in 3 steps of a single 360° isoclinic rotation, just as any single characteristic 5-cell reflecting itself in its own mirror walls generates the 24 vertices simultaneously by reflection.
Tracing the orbit of one such 16-cell vertex during the 360° isoclinic rotation reveals more about the relationship between reflections and rotations as generative operations.[lower-alpha 138] The vertex follows an isocline (a doubly curved geodesic circle) rather than any one of the singly curved geodesic circles that are the great circle segments over each √3 chord of the rotation.[lower-alpha 99] The isocline connects vertices two edge lengths apart, but curves away from the great circle path over the two edges connecting those vertices, missing the vertex in between.[lower-alpha 94] Although the isocline does not follow any one great circle, it is contained within a ring of another kind: in the 24-cell it stays within a 6-cell ring of spherical[72] octahedral cells, intersecting one vertex in each cell, and passing through the volume of two adjacent cells near the missed vertex.
Chiral symmetry operations
A symmetry operation is a rotation or reflection which leaves the object in a congruent orientation, indistinguishable from itself before the transformation. The 24-cell has 1152 distinct symmetry operations (576 rotations and 576 reflections). Each rotation is equivalent to two reflections, in a distinct pair of non-parallel mirror planes.[lower-alpha 138]
Pictured are sets of disjoint great circle polygons, each in a distinct central plane of the 24-cell. For example, {24/4}=4{6} is an orthogonal projection of the 24-cell picturing 4 of its [16] great hexagon planes.[lower-alpha 20] The 4 planes lie Clifford parallel to the projection plane and to each other, and their great polygons collectively constitute a discrete Hopf fibration of 4 non-intersecting great circles which visit all 24 vertices just once.
Each row of the table describes a class of distinct rotations. Each rotation class takes the left planes pictured to the corresponding right planes pictured.[lower-alpha 139] The vertices of the moving planes move in parallel along the skew polygonal isocline paths pictured. For example, the [math]\displaystyle{ [32]R_{q7,q8} }[/math] rotation class consists of [32] distinct rotational displacements by an arc-distance of 2𝝅/3 = 120° between 16 great hexagon planes represented by quaternion group [math]\displaystyle{ q7 }[/math] and a corresponding set of 16 great hexagon planes represented by quaternion group [math]\displaystyle{ q8 }[/math].[lower-alpha 141] One of the [32] distinct rotations of this class moves the representative vertex coordinate [math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] to the vertex coordinate [math]\displaystyle{ (\tfrac{1}{2},-\tfrac{1}{2},-\tfrac{1}{2},-\tfrac{1}{2}) }[/math].[lower-alpha 142]
| Proper rotations of the 24-cell symmetry group F4 [73] | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Isocline | Rotation class | Left planes [math]\displaystyle{ ql }[/math] | Right planes [math]\displaystyle{ qr }[/math] | |||||||||||
{24/8}=4{6/2}[lower-alpha 144]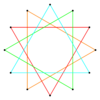 [16] 4𝝅 {6/2} |
[math]\displaystyle{ [32]R_{q7,q8} }[/math] | {24/4}=4{6}[lower-alpha 20] [16] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math][lower-alpha 142] | {24/4}=4{6}[lower-alpha 20] [16] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},-\tfrac{1}{2},-\tfrac{1}{2},-\tfrac{1}{2}) }[/math] | |||||||||
| 2𝝅/3 | 120° | √3 | 1.732~ | 𝝅/3 | 60° | √1 | 1 | 2𝝅/3 | 120° | √3 | 1.732~ | |||
{24/8}=4{6/2} [16] 4𝝅 {6/2} |
[math]\displaystyle{ [32]R_{q7,-q8} }[/math] | {24/4}=4{6} [16] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | {24/4}=4{6} [16] 2𝝅 {6} |
[math]\displaystyle{ (-\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | |||||||||
| 2𝝅/3 | 120° | √3 | 1.732~ | 𝝅/3 | 60° | √1 | 1 | 𝝅/3 | 60° | √1 | 1 | |||
{24/8}=4{6/2} [16] 4𝝅 {6/2} |
[math]\displaystyle{ [32]R_{q7,q7} }[/math] | {24/4}=4{6} [16] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | {24/4}=4{6} [16] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | |||||||||
| 2𝝅 | 360° | √0 | 0 | 𝝅/3 | 60° | √1 | 1 | 𝝅/3 | 60° | √1 | 1 | |||
{24/8}=4{6/2} [16] 4𝝅 {6/2} |
[math]\displaystyle{ [32]R_{q7,-q7} }[/math] | {24/4}=4{6} [16] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | {24/4}=4{6} [16] 2𝝅 {6} |
[math]\displaystyle{ (-\tfrac{1}{2},-\tfrac{1}{2},-\tfrac{1}{2},-\tfrac{1}{2}) }[/math] | |||||||||
| 𝝅 | 180° | √4 | 2 | 𝝅/3 | 60° | √1 | 1 | 2𝝅/3 | 120° | √3 | 1.732~ | |||
{24/4}=4{6} [8] 2𝝅 {6} |
[math]\displaystyle{ [16]R_{q7,q1} }[/math][lower-alpha 147] | {24/4}=4{6} [8] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | {24/6}=6{4}[lower-alpha 12] [8] 2𝝅 {4} |
[math]\displaystyle{ (1,0,0,0) }[/math] | |||||||||
| 𝝅/3 | 60° | √1 | 1 | 𝝅/3 | 60° | √1 | 1 | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/8}=4{6/2} [8] 4𝝅 {6/2} |
[math]\displaystyle{ [16]R_{q7,-q1} }[/math][lower-alpha 147] | {24/4}=4{6} [8] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | {24/6}=6{4} [8] 2𝝅 {4} |
[math]\displaystyle{ (-1,0,0,0) }[/math] | |||||||||
| 2𝝅/3 | 120° | √3 | 1.732~ | 𝝅/3 | 60° | √1 | 1 | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/9}=3{8/3}[lower-alpha 150]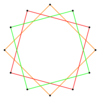 [9] 8𝝅 {8/3} |
[math]\displaystyle{ [36]R_{q6,q6} }[/math] | {24/6}=6{4} [18] 2𝝅 {4} |
[math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math][lower-alpha 152] | {24/6}=6{4} [18] 2𝝅 {4} |
[math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math] | |||||||||
| 2𝝅 | 360° | √0 | 0 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/9}=3{8/3} [9] 8𝝅 {8/3} |
[math]\displaystyle{ [36]R_{q6,-q6} }[/math] | {24/6}=6{4} [18] 2𝝅 {4} |
[math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math] | {24/6}=6{4} [18] 2𝝅 {4} |
[math]\displaystyle{ (-\tfrac{\sqrt{2}}{2},-\tfrac{\sqrt{2}}{2},0,0) }[/math] | |||||||||
| 𝝅 | 180° | √4 | 2 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/9}=3{8/3} [36] 8𝝅 {8/3} |
[math]\displaystyle{ [144]R_{q6,-q4} }[/math] | {24/6}=6{4} [72] 2𝝅 {4} |
[math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math] | {24/6}=6{4} [72] 2𝝅 {4} |
[math]\displaystyle{ (0,0,-\tfrac{\sqrt{2}}{2},-\tfrac{\sqrt{2}}{2}) }[/math] | |||||||||
| 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅 | 180° | √4 | 2 | |||
{24/9}=3{8/3} [18] 8𝝅 {8/3} |
[math]\displaystyle{ [72]R_{q4,q4} }[/math] | {24/6}=6{4} [36] 2𝝅 {4} |
[math]\displaystyle{ (0,0,\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2}) }[/math] | {24/6}=6{4} [36] 2𝝅 {4} |
[math]\displaystyle{ (0,0,\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2}) }[/math] | |||||||||
| 2𝝅 | 360° | √0 | 0 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/4}=4{6} [48] 2𝝅 {6} |
[math]\displaystyle{ [96]R_{q2,q7} }[/math][lower-alpha 147] | {24/6}=6{4} [48] 2𝝅 {4} |
[math]\displaystyle{ (0,0,0,1) }[/math] | {24/4}=4{6} [48] 2𝝅 {6} |
[math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] | |||||||||
| 𝝅/3 | 60° | √1 | 1 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/3 | 60° | √1 | 1 | |||
{24/6}=6{4} [9] 2𝝅 {4} |
[math]\displaystyle{ [18]R_{q2,-q2} }[/math] | {24/6}=6{4} [9] 2𝝅 {4} |
[math]\displaystyle{ (0,0,0,1) }[/math] | {24/6}=6{4} [9] 2𝝅 {4} |
[math]\displaystyle{ (0,0,0,-1) }[/math] | |||||||||
| 𝝅 | 180° | √4 | 2 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/12}=12{2} [12] 2𝝅 {2} |
[math]\displaystyle{ [12]R_{q2,q1} }[/math] | {24/12}=12{2} [12] 2𝝅 {2} |
[math]\displaystyle{ (0,0,0,1) }[/math] | {24/12}=12{2} [12] 2𝝅 {2} |
[math]\displaystyle{ (1,0,0,0) }[/math] | |||||||||
| 𝝅 | 180° | √4 | 2 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/12}=12{2} [0] 2𝝅 {2} |
[math]\displaystyle{ [1]R_{q1,q1} }[/math] | {24/12}=12{2} [0] 2𝝅 {2} |
[math]\displaystyle{ (1,0,0,0) }[/math] | {24/12}=12{2} [0] 2𝝅 {2} |
[math]\displaystyle{ (1,0,0,0) }[/math] | |||||||||
| 0 | 0° | √0 | 0 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
{24/12}=12{2} [12] 2𝝅 {2} |
[math]\displaystyle{ [1]R_{q1,-q1} }[/math] | {24/12}=12{2} [12] 2𝝅 {2} |
[math]\displaystyle{ (1,0,0,0) }[/math] | {24/12}=12{2} [12] 2𝝅 {2} |
[math]\displaystyle{ (-1,0,0,0) }[/math] | |||||||||
| 2𝝅 | 360° | √0 | 0 | 𝝅/2 | 90° | √2 | 1.414~ | 𝝅/2 | 90° | √2 | 1.414~ | |||
In a rotation class [math]\displaystyle{ [n]{R_{ql,qr}} }[/math] each quaternion group [math]\displaystyle{ \pm{q_n} }[/math] may be representative not only of its own fibration of Clifford parallel planes[lower-alpha 141] but also of the other congruent fibrations.[lower-alpha 20] For example, rotation class [math]\displaystyle{ [4]R_{q7,q8} }[/math] takes the 4 hexagon planes of [math]\displaystyle{ q7 }[/math] to the 4 hexagon planes of [math]\displaystyle{ q8 }[/math] in a 120° isoclinic rotation. But in a rigid rotation of this kind,[lower-alpha 153] all [16] hexagon planes move in congruent rotational displacements, so this rotation class also includes [math]\displaystyle{ [4]R_{-q7,-q8} }[/math], [math]\displaystyle{ [4]R_{q8,q7} }[/math] and [math]\displaystyle{ [4]R_{-q8,-q7} }[/math]. The name [math]\displaystyle{ [16]R_{q7,q8} }[/math] is the conventional representation for all [16] congruent plane displacements.
These rotation classes are all subclasses of [math]\displaystyle{ [32]R_{q7,q8} }[/math] which has [32] distinct rotational displacements rather than [16] because there are two chiral ways to perform any class of rotations, designated its left rotations and its right rotations. The [16] left displacements of this class are not congruent with the [16] right displacements, but enantiamorphous like a pair of shoes.[lower-alpha 154] Each left (or right) isoclinic rotation takes [16] left planes to [16] right planes, but the left and right planes correspond differently in the left and right rotations. The left and right rotational displacements of the same left plane take it to different right planes.
Each rotation class (table row) describes a distinct left (and right) isoclinic rotation. The left (or right) rotation carries the left planes to the right planes through a characteristic rotation angle. For example, the [math]\displaystyle{ [32]R_{q7,q8} }[/math] rotation moves [16] planes by 2𝝅/3 = 120° each. Repeated 6 times, this left (or right) isoclinic rotation moves each plane 720° and back to itself in the same orientation, passing through all 4 planes of the [math]\displaystyle{ q7 }[/math] left set and all 4 planes of the [math]\displaystyle{ q8 }[/math] right set once each.[lower-alpha 140] The picture in the isocline column represents this union of the left and right plane sets. In the [math]\displaystyle{ [32]R_{q7,q8} }[/math] example it can be seen as a set of 4 Clifford parallel skew hexagrams, each having one edge in each great hexagon plane, and skewing to the left (or right) at each vertex throughout the left (or right) isoclinic rotation.[lower-alpha 144]
Visualization

Cell rings
The 24-cell is bounded by 24 octahedral cells. For visualization purposes, it is convenient that the octahedron has opposing parallel faces (a trait it shares with the cells of the tesseract and the 120-cell). One can stack octahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 6 cells.[74][75] The cell locations lend themselves to a hyperspherical description. Pick an arbitrary cell and label it the "North Pole". Eight great circle meridians (two cells long) radiate out in 3 dimensions, converging at the 3rd "South Pole" cell. This skeleton accounts for 18 of the 24 cells (2 + 8×2). See the table below.
There is another related great circle in the 24-cell, the dual of the one above. A path that traverses 6 vertices solely along edges resides in the dual of this polytope, which is itself since it is self dual. These are the hexagonal geodesics described above.[lower-alpha 40] One can easily follow this path in a rendering of the equatorial cuboctahedron cross-section.
Starting at the North Pole, we can build up the 24-cell in 5 latitudinal layers. With the exception of the poles, each layer represents a separate 2-sphere, with the equator being a great 2-sphere.[lower-alpha 45] The cells labeled equatorial in the following table are interstitial to the meridian great circle cells. The interstitial "equatorial" cells touch the meridian cells at their faces. They touch each other, and the pole cells at their vertices. This latter subset of eight non-meridian and pole cells has the same relative position to each other as the cells in a tesseract (8-cell), although they touch at their vertices instead of their faces.
| Layer # | Number of Cells | Description | Colatitude | Region |
|---|---|---|---|---|
| 1 | 1 cell | North Pole | 0° | Northern Hemisphere |
| 2 | 8 cells | First layer of meridian cells | 60° | |
| 3 | 6 cells | Non-meridian / interstitial | 90° | Equator |
| 4 | 8 cells | Second layer of meridian cells | 120° | Southern Hemisphere |
| 5 | 1 cell | South Pole | 180° | |
| Total | 24 cells | |||
The 24-cell can be partitioned into cell-disjoint sets of four of these 6-cell great circle rings, forming a discrete Hopf fibration of four interlocking rings.[lower-alpha 110] One ring is "vertical", encompassing the pole cells and four meridian cells. The other three rings each encompass two equatorial cells and four meridian cells, two from the northern hemisphere and two from the southern.[76]
Note this hexagon great circle path implies the interior/dihedral angle between adjacent cells is 180 - 360/6 = 120 degrees. This suggests you can adjacently stack exactly three 24-cells in a plane and form a 4-D honeycomb of 24-cells as described previously.
One can also follow a great circle route, through the octahedrons' opposing vertices, that is four cells long. These are the square geodesics along four √2 chords described above. This path corresponds to traversing diagonally through the squares in the cuboctahedron cross-section. The 24-cell is the only regular polytope in more than two dimensions where you can traverse a great circle purely through opposing vertices (and the interior) of each cell. This great circle is self dual. This path was touched on above regarding the set of 8 non-meridian (equatorial) and pole cells.
The 24-cell can be equipartitioned into three 8-cell subsets, each having the organization of a tesseract. Each of these subsets can be further equipartitioned into two interlocking great circle chains, four cells long. Collectively these three subsets now produce another, six ring, discrete Hopf fibration.
Parallel projections
The vertex-first parallel projection of the 24-cell into 3-dimensional space has a rhombic dodecahedral envelope. Twelve of the 24 octahedral cells project in pairs onto six square dipyramids that meet at the center of the rhombic dodecahedron. The remaining 12 octahedral cells project onto the 12 rhombic faces of the rhombic dodecahedron.
The cell-first parallel projection of the 24-cell into 3-dimensional space has a cuboctahedral envelope. Two of the octahedral cells, the nearest and farther from the viewer along the w-axis, project onto an octahedron whose vertices lie at the center of the cuboctahedron's square faces. Surrounding this central octahedron lie the projections of 16 other cells, having 8 pairs that each project to one of the 8 volumes lying between a triangular face of the central octahedron and the closest triangular face of the cuboctahedron. The remaining 6 cells project onto the square faces of the cuboctahedron. This corresponds with the decomposition of the cuboctahedron into a regular octahedron and 8 irregular but equal octahedra, each of which is in the shape of the convex hull of a cube with two opposite vertices removed.
The edge-first parallel projection has an elongated hexagonal dipyramidal envelope, and the face-first parallel projection has a nonuniform hexagonal bi-antiprismic envelope.
Perspective projections
The vertex-first perspective projection of the 24-cell into 3-dimensional space has a tetrakis hexahedral envelope. The layout of cells in this image is similar to the image under parallel projection.
The following sequence of images shows the structure of the cell-first perspective projection of the 24-cell into 3 dimensions. The 4D viewpoint is placed at a distance of five times the vertex-center radius of the 24-cell.
 Animated cross-section of 24-cell | ||
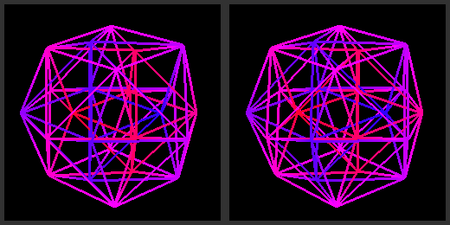 A stereoscopic 3D projection of an icositetrachoron (24-cell). | ||
| File:Cell24Construction.ogv Isometric Orthogonal Projection of: 8 Cell(Tesseract) + 16 Cell = 24 Cell | ||
Related polytopes
Three Coxeter group constructions
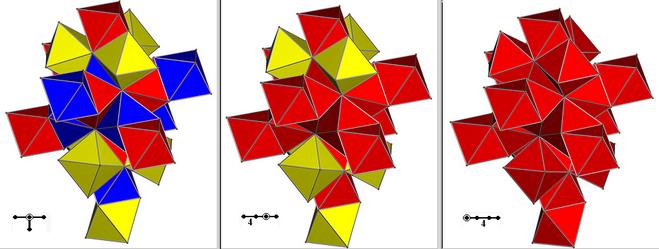
There are two lower symmetry forms of the 24-cell, derived as a rectified 16-cell, with B4 or [3,3,4] symmetry drawn bicolored with 8 and 16 octahedral cells. Lastly it can be constructed from D4 or [31,1,1] symmetry, and drawn tricolored with 8 octahedra each.
| Three nets of the 24-cell with cells colored by D4, B4, and F4 symmetry | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Rectified demitesseract | Rectified 16-cell | Regular 24-cell | |||||||||
| D4, [31,1,1], order 192 | B4, [3,3,4], order 384 | F4, [3,4,3], order 1152 | |||||||||
| |||||||||||
| Three sets of 8 rectified tetrahedral cells | One set of 16 rectified tetrahedral cells and one set of 8 octahedral cells. | One set of 24 octahedral cells | |||||||||
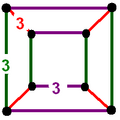
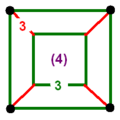
| Vertex figure (Each edge corresponds to one triangular face, colored by symmetry arrangement) | |||||||||||
|
|

| |||||||||
Related complex polygons
The regular complex polygon 4{3}4, ![]()
![]()
![]() or
or ![]()
![]()
![]() contains the 24 vertices of the 24-cell, and 24 4-edges that correspond to central squares of 24 of 48 octahedral cells. Its symmetry is 4[3]4, order 96.[77]
contains the 24 vertices of the 24-cell, and 24 4-edges that correspond to central squares of 24 of 48 octahedral cells. Its symmetry is 4[3]4, order 96.[77]
The regular complex polytope 3{4}3, ![]()
![]()
![]() or
or ![]()
![]()
![]() , in [math]\displaystyle{ \mathbb{C}^2 }[/math] has a real representation as a 24-cell in 4-dimensional space. 3{4}3 has 24 vertices, and 24 3-edges. Its symmetry is 3[4]3, order 72.
, in [math]\displaystyle{ \mathbb{C}^2 }[/math] has a real representation as a 24-cell in 4-dimensional space. 3{4}3 has 24 vertices, and 24 3-edges. Its symmetry is 3[4]3, order 72.
Related 4-polytopes
Several uniform 4-polytopes can be derived from the 24-cell via truncation:
- truncating at 1/3 of the edge length yields the truncated 24-cell;
- truncating at 1/2 of the edge length yields the rectified 24-cell;
- and truncating at half the depth to the dual 24-cell yields the bitruncated 24-cell, which is cell-transitive.
The 96 edges of the 24-cell can be partitioned into the golden ratio to produce the 96 vertices of the snub 24-cell. This is done by first placing vectors along the 24-cell's edges such that each two-dimensional face is bounded by a cycle, then similarly partitioning each edge into the golden ratio along the direction of its vector. An analogous modification to an octahedron produces an icosahedron, or "snub octahedron."
The 24-cell is the unique convex self-dual regular Euclidean polytope that is neither a polygon nor a simplex. Relaxing the condition of convexity admits two further figures: the great 120-cell and grand stellated 120-cell. With itself, it can form a polytope compound: the compound of two 24-cells.
Related uniform polytopes
The 24-cell can also be derived as a rectified 16-cell:
See also
- Octacube (sculpture)
- Uniform 4-polytope § The F4 family
Notes
- ↑ The 24-cell is one of only three self-dual regular Euclidean polytopes which are neither a polygon nor a simplex. The other two are also 4-polytopes, but not convex: the grand stellated 120-cell and the great 120-cell. The 24-cell is nearly unique among self-dual regular convex polytopes in that it and the even polygons are the only such polytopes where a face is not opposite an edge.
- ↑ Jump up to: 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 The long radius (center to vertex) of the 24-cell is equal to its edge length; thus its long diameter (vertex to opposite vertex) is 2 edge lengths. Only a few uniform polytopes have this property, including the four-dimensional 24-cell and tesseract, the three-dimensional cuboctahedron, and the two-dimensional hexagon. (The cuboctahedron is the equatorial cross section of the 24-cell, and the hexagon is the equatorial cross section of the cuboctahedron.) Radially equilateral polytopes are those which can be constructed, with their long radii, from equilateral triangles which meet at the center of the polytope, each contributing two radii and an edge.
- ↑ Jump up to: 3.0 3.1 The convex regular polytopes in the first four dimensions with a 5 in their Schlӓfli symbol are the pentagon {5}, the icosahedron {3, 5}, the dodecahedron {5, 3}, the 600-cell {3,3,5} and the 120-cell {5,3,3}. In other words, the 24-cell possesses all of the triangular and square features that exist in four dimensions except the regular 5-cell, but none of the pentagonal features. (The 5-cell {3, 3, 3} is also pentagonal in the sense that its Petrie polygon is the pentagon.)
- ↑ The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more content[7] within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. This provides an alternative numerical naming scheme for regular polytopes in which the 24-cell is the 24-point 4-polytope: fourth in the ascending sequence that runs from 5-point 4-polytope to 600-point 4-polytope.
- ↑ The edge length will always be different unless predecessor and successor are both radially equilateral, i.e. their edge length is the same as their radius (so both are preserved). Since radially equilateral polytopes[lower-alpha 2] are rare, it seems that the only such construction (in any dimension) is from the 8-cell to the 24-cell, making the 24-cell the unique regular polytope (in any dimension) which has the same edge length as its predecessor of the same radius.
- ↑ The edges of six of the squares are aligned with the grid lines of the √2 radius coordinate system. For example:
( 0, −1, 1, 0) ( 0, 1, 1, 0)
( 0, −1, −1, 0) ( 0, 1, −1, 0)
is the square in the xy plane. The edges of the squares are not 24-cell edges, they are interior chords joining two vertices 90o distant from each other; so the squares are merely invisible configurations of four of the 24-cell's vertices, not visible 24-cell features. - ↑ Jump up to: 7.00 7.01 7.02 7.03 7.04 7.05 7.06 7.07 7.08 7.09 7.10 Two flat planes A and B of a Euclidean space of four dimensions are called completely orthogonal if and only if every line in A is orthogonal to every line in B. In that case the planes A and B intersect at a single point O, so that if a line in A intersects with a line in B, they intersect at O. A and B are perpendicular and Clifford parallel.[lower-alpha 10]
- ↑ Up to 6 planes can be mutually orthogonal in 4 dimensions. 3 dimensional space accommodates only 3 perpendicular axes and 3 perpendicular planes through a single point. In 4 dimensional space we may have 4 perpendicular axes and 6 perpendicular planes through a point (for the same reason that the tetrahedron has 6 edges, not 4): there are 6 ways to take 4 dimensions 2 at a time. Three such perpendicular planes (pairs of axes) meet at each vertex of the 24-cell (for the same reason that three edges meet at each vertex of the tetrahedron). Each of the 6 planes is completely orthogonal[lower-alpha 7] to just one of the other planes: the only one with which it does not share a line (for the same reason that each edge of the tetrahedron is orthogonal to just one of the other edges: the only one with which it does not share a point). Two completely orthogonal planes are perpendicular and opposite each other, as two edges of the tetrahedron are perpendicular and opposite.
- ↑ Jump up to: 9.0 9.1 To visualize how two planes can intersect in a single point in a four dimensional space, consider the Euclidean space (w, x, y, z) and imagine that the w dimension represents time rather than a spatial dimension. The xy central plane (where w=0, z=0) shares no axis with the wz central plane (where x=0, y=0). The xy plane exists at only a single instant in time (w=0); the wz plane (and in particular the w axis) exists all the time. Thus their only moment and place of intersection is at the origin point (0,0,0,0).
- ↑ Jump up to: 10.0 10.1 10.2 10.3 10.4 10.5 In 4 dimensional space we can construct 4 perpendicular axes and 6 perpendicular planes through a point. Without loss of generality, we may take these to be the axes and orthogonal central planes of a (w, x, y, z) Cartesian coordinate system. In 4 dimensions we have the same 3 orthogonal planes (xy, xz, yz) that we have in 3 dimensions, and also 3 others (wx, wy, wz). Each of the 6 orthogonal planes shares an axis with 4 of the others, and is completely orthogonal to just one of the others: the only one with which it does not share an axis. Thus there are 3 pairs of completely orthogonal planes: xy and wz intersect only at the origin; xz and wy intersect only at the origin; yz and wx intersect only at the origin.
- ↑ Jump up to: 11.0 11.1 11.2 11.3 11.4 Two planes in 4-dimensional space can have four possible reciprocal positions: (1) they can coincide (be exactly the same plane); (2) they can be parallel (the only way they can fail to intersect at all); (3) they can intersect in a single line, as two non-parallel planes do in 3-dimensional space; or (4) they can intersect in a single point[lower-alpha 9] (and they must, if they are completely orthogonal).[lower-alpha 7]
- ↑ Jump up to: 12.0 12.1 12.2 12.3 12.4 There are 3 sets of 6 disjoint great squares in the 24-cell (of a total of [18] distinct great squares),[lower-alpha 148] designated [math]\displaystyle{ \pm q1 }[/math], [math]\displaystyle{ \pm q2 }[/math], and [math]\displaystyle{ \pm q3 }[/math]. Each named set[lower-alpha 149] of 6 Clifford parallel squares comprises a discrete fibration covering all 24 vertices.
- ↑ Jump up to: 13.0 13.1 13.2 13.3 In four-dimensional Euclidean geometry, a quaternion is simply a (w, x, y, z) Cartesian coordinate. Hamilton did not see them as such when he discovered the quaternions. Schläfli would be the first to consider four-dimensional Euclidean space, publishing his discovery of the regular polyschemes in 1852, but Hamilton would never be influenced by that work, which remained obscure into the 20th century. Hamilton found the quaternions when he realized that a fourth dimension, in some sense, would be necessary in order to model rotations in three-dimensional space.[36] Although he described a quaternion as an ordered four-element multiple of real numbers, the quaternions were for him an extension of the complex numbers, not a Euclidean space of four dimensions.
- ↑ The edges of the orthogonal great squares are not aligned with the grid lines of the unit radius coordinate system. Six of the squares do lie in the 6 orthogonal planes of this coordinate system, but their edges are the √2 diagonals of unit edge length squares of the coordinate lattice. For example:
( 0, 0, 1, 0)
( 0, −1, 0, 0) ( 0, 1, 0, 0)
( 0, 0, −1, 0)
is the square in the xy plane. Notice that the 8 integer coordinates comprise the vertices of the 6 orthogonal squares. - ↑ Jump up to: 15.0 15.1 15.2 15.3 15.4 15.5 15.6 In an isoclinic rotation, each point anywhere in the 4-polytope moves an equal distance in four orthogonal directions at once, on a 4-dimensional diagonal. The point is displaced a total Pythagorean distance equal to the square root of four times the square of that distance. All vertices are displaced to a vertex at least two edge lengths away.[lower-alpha 21] For example, when the unit-radius 24-cell rotates isoclinically 60° in a hexagon invariant plane and 60° in its completely orthogonal invariant plane,[lower-alpha 55] each vertex is displaced to another vertex √3 (120°) away, moving √3/4 ≈ 0.866 in four orthogonal directions.
- ↑ Jump up to: 16.0 16.1 16.2 Each great hexagon of the 24-cell contains one axis (one pair of antipodal vertices) belonging to each of the three inscribed 16-cells. The 24-cell contains three disjoint inscribed 16-cells, rotated 60° isoclinically[lower-alpha 15] with respect to each other (so their corresponding vertices are 120° = √3 apart). A 16-cell is an orthonormal basis for a 4-dimensional coordinate system, because its 8 vertices define the four orthogonal axes. In any choice of a vertex-up coordinate system (such as the unit radius coordinates used in this article), one of the three inscribed 16-cells is the basis for the coordinate system, and each hexagon has only one axis which is a coordinate system axis.
- ↑ Jump up to: 17.0 17.1 17.2 17.3 17.4 The hexagons are inclined (tilted) at 60 degrees with respect to the unit radius coordinate system's orthogonal planes. Each hexagonal plane contains only one of the 4 coordinate system axes.[lower-alpha 16] The hexagon consists of 3 pairs of opposite vertices (three 24-cell diameters): one opposite pair of integer coordinate vertices (one of the four coordinate axes), and two opposite pairs of half-integer coordinate vertices (not coordinate axes). For example:
( 0, 0, 1, 0)
( 1/2, −1/2, 1/2, −1/2) ( 1/2, 1/2, 1/2, 1/2)
(−1/2, −1/2, −1/2, −1/2) (−1/2, 1/2, −1/2, 1/2)
( 0, 0, −1, 0)
is a hexagon on the y axis. Unlike the √2 squares, the hexagons are actually made of 24-cell edges, so they are visible features of the 24-cell. - ↑ Jump up to: 18.0 18.1 18.2 Eight √1 edges converge in curved 3-dimensional space from the corners of the 24-cell's cubical vertex figure[lower-alpha 38] and meet at its center (the vertex), where they form 4 straight lines which cross there. The 8 vertices of the cube are the eight nearest other vertices of the 24-cell. The straight lines are geodesics: two √1-length segments of an apparently straight line (in the 3-space of the 24-cell's curved surface) that is bent in the 4th dimension into a great circle hexagon (in 4-space). Imagined from inside this curved 3-space, the bends in the hexagons are invisible. From outside (if we could view the 24-cell in 4-space), the straight lines would be seen to bend in the 4th dimension at the cube centers, because the center is displaced outward in the 4th dimension, out of the hyperplane defined by the cube's vertices. Thus the vertex cube is actually a cubic pyramid. Unlike a cube, it seems to be radially equilateral (like the tesseract and the 24-cell itself): its "radius" equals its edge length.[lower-alpha 39]
- ↑ Jump up to: 19.0 19.1 19.2 19.3 It is not difficult to visualize four hexagonal planes intersecting at 60 degrees to each other, even in three dimensions. Four hexagonal central planes intersect at 60 degrees in the cuboctahedron. Four of the 24-cell's 16 hexagonal central planes (lying in the same 3-dimensional hyperplane) intersect at each of the 24-cell's vertices exactly the way they do at the center of a cuboctahedron. But the edges around the vertex do not meet as the radii do at the center of a cuboctahedron; the 24-cell has 8 edges around each vertex, not 12, so its vertex figure is the cube, not the cuboctahedron. The 8 edges meet exactly the way 8 edges do at the apex of a canonical cubic pyramid.[lower-alpha 18]
- ↑ Jump up to: 20.0 20.1 20.2 20.3 20.4 20.5 20.6 20.7 20.8 20.9 There are 4 sets of 4 disjoint great hexagons in the 24-cell (of a total of [16] distinct great hexagons), designated [math]\displaystyle{ q7 }[/math], [math]\displaystyle{ -q7 }[/math], [math]\displaystyle{ q8 }[/math] and [math]\displaystyle{ -q8 }[/math].[lower-alpha 140] Each named set of 4 Clifford parallel hexagons comprises a discrete fibration covering all 24 vertices.
- ↑ Jump up to: 21.0 21.1 21.2 21.3 21.4 21.5 21.6 21.7 21.8 21.9 In an isoclinic rotation vertices move diagonally, like the bishops in chess. Vertices in an isoclinic rotation cannot reach any of their nearest neighbor vertices because they do not rotate directly toward them;[lower-alpha 29] they move diagonally between them, missing them, to a vertex farther away in a larger-radius surrounding shell of vertices,[lower-alpha 31] the way bishops are confined to the white or black squares of the chessboard and cannot reach squares of the opposite color, even those immediately adjacent.[lower-alpha 93] Things moving diagonally move farther than 1 unit of distance in each movement step (√2 on the chessboard, √3 in the 24-cell), but at the cost of missing half the destinations.[lower-alpha 82] However in an isoclinic rotation of a rigid body all the vertices rotate at once, so every destination will be reached by some vertex.
- ↑ Jump up to: 22.0 22.1 22.2 22.3 22.4 22.5 22.6 22.7 22.8 22.9 The 24-cell contains 3 distinct 8-cells (tesseracts), rotated 60° isoclinically with respect to each other. The corresponding vertices of two 8-cells are √3 (120°) apart. Each 8-cell contains 8 cubical cells, and each cube contains four √3 chords (its long diameters). The 8-cells are not completely disjoint (they share vertices),[lower-alpha 25] but each cube and each √3 chord belongs to just one 8-cell. The √3 chords joining the corresponding vertices of two 8-cells belong to the third 8-cell.[lower-alpha 31]
- ↑ Jump up to: 23.0 23.1 These triangles' edges of length √3 are the diagonals[lower-alpha 21] of cubical cells of unit edge length found within the 24-cell, but those cubical (tesseract)[lower-alpha 22] cells are not cells of the unit radius coordinate lattice.
- ↑ Jump up to: 24.0 24.1 These triangles lie in the same planes containing the hexagons;[lower-alpha 17] two triangles of edge length √3 are inscribed in each hexagon. For example, in unit radius coordinates:
( 0, 0, 1, 0)
( 1/2, −1/2, 1/2, −1/2) ( 1/2, 1/2, 1/2, 1/2)
(−1/2, −1/2, −1/2, −1/2) (−1/2, 1/2, −1/2, 1/2)
( 0, 0, −1, 0)
are two opposing central triangles on the y axis, with each triangle formed by the vertices in alternating rows. Unlike the hexagons, the √3 triangles are not made of actual 24-cell edges, so they are invisible features of the 24-cell, like the √2 squares. - ↑ Jump up to: 25.0 25.1 25.2 25.3 25.4 25.5 Polytopes are completely disjoint if all their element sets are disjoint: they do not share any vertices, edges, faces or cells. They may still overlap in space, sharing 4-content, volume, area, or lineage.
- ↑ Jump up to: 26.0 26.1 26.2 Visualize the three 16-cells inscribed in the 24-cell (left, right, and middle), and the rotation which takes them to each other. The vertices of the middle 16-cell lie on the (w, x, y, z) coordinate axes;[lower-alpha 10] the other two are rotated 60° isoclinically to its left and its right. The 24-vertex 24-cell is a compound of three 16-cells, whose three sets of 8 vertices are distributed around the 24-cell symmetrically; each vertex is surrounded by 8 others (in the 3-dimensional space of the 4-dimensional 24-cell's surface), the way the vertices of a cube surround its center.[lower-alpha 18] The 8 surrounding vertices (the cube corners) lie in other 16-cells: 4 in the other 16-cell to the left, and 4 in the other 16-cell to the right. They are the vertices of two tetrahedra inscribed in the cube, one belonging (as a cell) to each 16-cell. If the 16-cell edges are √2, each vertex of the compound of three 16-cells is √1 away from its 8 surrounding vertices in other 16-cells. Now visualize those √1 distances as the edges of the 24-cell (while continuing to visualize the disjoint 16-cells). The √1 edges form great hexagons of 6 vertices which run around the 24-cell in a central plane. Four hexagons cross at each vertex (and its antipodal vertex), inclined at 60° to each other.[lower-alpha 19] The hexagons are not perpendicular to each other, or to the 16-cells' perpendicular square central planes.[lower-alpha 17] The left and right 16-cells form a tesseract.[lower-alpha 27] Two 16-cells have vertex-pairs which are one √1 edge (one hexagon edge) apart. But a simple rotation of 60° will not take one whole 16-cell to another 16-cell, because their vertices are 60° apart in different directions, and a simple rotation has only one hexagonal plane of rotation. One 16-cell can be taken to another 16-cell by a 60° isoclinic rotation, because an isoclinic rotation is 3-sphere symmetric: four Clifford parallel hexagonal planes rotate together, but in four different rotational directions,[lower-alpha 80] taking each 16-cell to another 16-cell. But since an isoclinic 60° rotation is a diagonal rotation by 60° in two orthogonal great circles at once,[lower-alpha 49] the corresponding vertices of the 16-cell and the 16-cell it is taken to are 120° apart: two √1 hexagon edges (or one √3 hexagon chord) apart, not one √1 edge (60°) apart.[lower-alpha 15] By the chiral diagonal nature of isoclinic rotations, the 16-cell cannot reach the adjacent 16-cell (whose vertices are one √1 edge away) by rotating toward it;[lower-alpha 21] it can only reach the 16-cell beyond it (120° away). But of course, the 16-cell beyond the 16-cell to its right is the 16-cell to its left. So a 60° isoclinic rotation will take every 16-cell to another 16-cell: a 60° right isoclinic rotation will take the middle 16-cell to the 16-cell we may have originally visualized as the left 16-cell, and a 60° left isoclinic rotation will take the middle 16-cell to the 16-cell we visualized as the right 16-cell. (If so, that was our error in visualization; the 16-cell to the "left" is in fact the one reached by the left isoclinic rotation, as that is the only sense in which the two 16-cells are left or right of each other.)[lower-alpha 85]
- ↑ Jump up to: 27.0 27.1 27.2 27.3 Each pair of the three 16-cells inscribed in the 24-cell forms a 4-dimensional hypercube (a tesseract or 8-cell), in dimensional analogy to the way two tetrahedra form a cube: the two 8-vertex 16-cells are inscribed in the 16-vertex tesseract, occupying its alternate vertices. The third 16-cell does not lie within the tesseract; its 8 vertices protrude from the sides of the tesseract, forming a cubic pyramid on each of the tesseract's cubic cells (as in Gosset's construction of the 24-cell). The three pairs of 16-cells form three tesseracts.[lower-alpha 22] The tesseracts share vertices, but the 16-cells are completely disjoint.[lower-alpha 25]
- ↑ Jump up to: 28.0 28.1 The 18 great squares of the 24-cell occur as three sets of 6 orthogonal great squares,[lower-alpha 10] each forming a 16-cell.[lower-alpha 26] The three 16-cells are completely disjoint (and Clifford parallel): each has its own 8 vertices (on 4 orthogonal axes) and its own 24 edges (of length √2). The 18 square great circles are crossed by 16 hexagonal great circles; each hexagon has one axis (2 vertices) in each 16-cell.[lower-alpha 17] The two great triangles inscribed in each great hexagon (occupying its alternate vertices, and with edges that are its √3 chords) have one vertex in each 16-cell. Thus each great triangle is a ring linking the three completely disjoint 16-cells. There are four different ways (four different fibrations of the 24-cell) in which the 8 vertices of the 16-cells correspond by being triangles of vertices √3 apart: there are 32 distinct linking triangles. Each pair of 16-cells forms a tesseract (8-cell).[lower-alpha 27] Each great triangle has one √3 edge in each tesseract, so it is also a ring linking the three tesseracts.
- ↑ Jump up to: 29.0 29.1 The 8 nearest neighbor vertices surround the vertex (in the curved 3-dimensional space of the 24-cell's boundary surface) the way a cube's 8 corners surround its center. (The vertex figure of the 24-cell is a cube.)
- ↑ The 6 second-nearest neighbor vertices surround the vertex in curved 3-dimensional space the way an octahedron's 6 corners surround its center.
- ↑ Jump up to: 31.0 31.1 31.2 31.3 Eight √3 chords converge from the corners of the 24-cell's cubical vertex figure[lower-alpha 38] and meet at its center (the vertex), where they form 4 straight lines which cross there. Each of the eight √3 chords runs from this cube's center to the center of a diagonally adjacent (vertex-bonded) cube,[lower-alpha 21] which is another vertex of the 24-cell: one located 120° away in a third concentric shell of eight √3-distant vertices surrounding the second shell of six √2-distant vertices that surrounds the first shell of eight √1-distant vertices.
- ↑ Jump up to: 32.0 32.1 32.2 32.3 Interior features are not considered elements of the polytope. For example, the center of a 24-cell is a noteworthy feature (as are its long radii), but these interior features do not count as elements in its configuration matrix, which counts only elementary features (which are not interior to any other feature including the polytope itself). Interior features are not rendered in most of the diagrams and illustrations in this article (they are normally invisible). In illustrations showing interior features, we always draw interior edges as dashed lines, to distinguish them from elementary edges.
- ↑ Jump up to: 33.0 33.1 33.2 The center of the regular 24-cell is a canonical apex of the 24-cell because it is one edge length equidistant from the 24 ordinary vertices in the 4th dimension, as the apex of a canonical pyramid is one edge length equidistant from its other vertices.
- ↑ Thus (√1, √2, √3, √4) are the vertex chord lengths of the tesseract as well as of the 24-cell. They are also the diameters of the tesseract (from short to long), though not of the 24-cell.
- ↑ Jump up to: 35.00 35.01 35.02 35.03 35.04 35.05 35.06 35.07 35.08 35.09 35.10 35.11 35.12 35.13 35.14 Clifford parallels are non-intersecting curved lines that are parallel in the sense that the perpendicular (shortest) distance between them is the same at each point.[14] A double helix is an example of Clifford parallelism in ordinary 3-dimensional Euclidean space. In 4-space Clifford parallels occur as geodesic great circles on the 3-sphere.[15] Whereas in 3-dimensional space, any two geodesic great circles on the 2-sphere will always intersect at two antipodal points, in 4-dimensional space not all great circles intersect; various sets of Clifford parallel non-intersecting geodesic great circles can be found on the 3-sphere. Perhaps the simplest example is that six mutually orthogonal great circles can be drawn on the 3-sphere, as three pairs of completely orthogonal great circles.[lower-alpha 10] Each completely orthogonal pair is Clifford parallel. The two circles cannot intersect at all, because they lie in planes which intersect at only one point: the center of the 3-sphere.[lower-alpha 44] Because they are perpendicular and share a common center,[lower-alpha 45] the two circles are obviously not parallel and separate in the usual way of parallel circles in 3 dimensions; rather they are connected like adjacent links in a chain, each passing through the other without intersecting at any points, forming a Hopf link.
- ↑ A geodesic great circle lies in a 2-dimensional plane which passes through the center of the polytope. Notice that in 4 dimensions this central plane does not bisect the polytope into two equal-sized parts, as it would in 3 dimensions, just as a diameter (a central line) bisects a circle but does not bisect a sphere. Another difference is that in 4 dimensions not all pairs of great circles intersect at two points, as they do in 3 dimensions; some pairs do, but some pairs of great circles are non-intersecting Clifford parallels.[lower-alpha 35]
- ↑ Jump up to: 37.0 37.1 If the Pythagorean distance between any two vertices is √1, their geodesic distance is 1; they may be two adjacent vertices (in the curved 3-space of the surface), or a vertex and the center (in 4-space). If their Pythagorean distance is √2, their geodesic distance is 2 (whether via 3-space or 4-space, because the path along the edges is the same straight line with one 90o bend in it as the path through the center). If their Pythagorean distance is √3, their geodesic distance is still 2 (whether on a hexagonal great circle past one 60o bend, or as a straight line with one 60o bend in it through the center). Finally, if their Pythagorean distance is √4, their geodesic distance is still 2 in 4-space (straight through the center), but it reaches 3 in 3-space (by going halfway around a hexagonal great circle).
- ↑ Jump up to: 38.0 38.1 38.2 38.3 38.4 The vertex figure is the facet which is made by truncating a vertex; canonically, at the mid-edges incident to the vertex. But one can make similar vertex figures of different radii by truncating at any point along those edges, up to and including truncating at the adjacent vertices to make a full size vertex figure. Stillwell defines the vertex figure as "the convex hull of the neighbouring vertices of a given vertex".[13] That is what serves the illustrative purpose here.
- ↑ The cube is not radially equilateral in Euclidean 3-space [math]\displaystyle{ \mathbb{R}^3 }[/math], but a cubic pyramid is radially equilateral in the curved 3-space of the 24-cell's surface, the 3-sphere [math]\displaystyle{ \mathbb{S}^3 }[/math]. In 4-space the 8 edges radiating from its apex are not actually its radii: the apex of the cubic pyramid is not actually its center, just one of its vertices. But in curved 3-space the edges radiating symmetrically from the apex are radii, so the cube is radially equilateral in that curved 3-space [math]\displaystyle{ \mathbb{S}^3 }[/math]. In Euclidean 4-space [math]\displaystyle{ \mathbb{R}^4 }[/math] 24 edges radiating symmetrically from a central point make the radially equilateral 24-cell,[lower-alpha 2] and a symmetrical subset of 16 of those edges make the radially equilateral tesseract.
- ↑ Jump up to: 40.0 40.1 40.2 40.3 40.4 40.5 40.6 The 24-cell has four sets of 4 non-intersecting Clifford parallel[lower-alpha 35] great circles each passing through 6 vertices (a great hexagon), with only one great hexagon in each set passing through each vertex, and the 4 hexagons in each set reaching all 24 vertices.[lower-alpha 20] Each set constitutes a discrete Hopf fibration of interlocking great circles. The 24-cell can also be divided (eight different ways) into 4 disjoint subsets of 6 vertices (hexagrams) that do not lie in a hexagonal central plane, each skew hexagram forming an isoclinic geodesic or isocline that is the rotational circle traversed by those 6 vertices in one particular left or right isoclinic rotation. Each of these sets of four Clifford parallel isoclines belongs to one of the four discrete Hopf fibrations of hexagonal great circles.[lower-alpha 109]
- ↑ Six √2 chords converge in 3-space from the face centers of the 24-cell's cubical vertex figure[lower-alpha 38] and meet at its center (the vertex), where they form 3 straight lines which cross there perpendicularly. The 8 vertices of the cube are the eight nearest other vertices of the 24-cell, and eight √1 edges converge from there, but let us ignore them now, since 7 straight lines crossing at the center is confusing to visualize all at once. Each of the six √2 chords runs from this cube's center (the vertex) through a face center to the center of an adjacent (face-bonded) cube, which is another vertex of the 24-cell: not a nearest vertex (at the cube corners), but one located 90° away in a second concentric shell of six √2-distant vertices that surrounds the first shell of eight √1-distant vertices. The face-center through which the √2 chord passes is the mid-point of the √2 chord, so it lies inside the 24-cell.
- ↑ One can cut the 24-cell through 6 vertices (in any hexagonal great circle plane), or through 4 vertices (in any square great circle plane). One can see this in the cuboctahedron (the central hyperplane of the 24-cell), where there are four hexagonal great circles (along the edges) and six square great circles (across the square faces diagonally).
- ↑ Jump up to: 43.0 43.1 43.2 43.3 In the 16-cell the 6 orthogonal great squares form 3 pairs of completely orthogonal great circles; each pair is Clifford parallel. In the 24-cell, the 3 inscribed 16-cells lie rotated 60 degrees isoclinically[lower-alpha 15] with respect to each other; consequently their corresponding vertices are 120 degrees apart on a hexagonal great circle. Pairing their vertices which are 90 degrees apart reveals corresponding square great circles which are Clifford parallel. Each of the 18 square great circles is Clifford parallel not only to one other square great circle in the same 16-cell (the completely orthogonal one), but also to two square great circles (which are completely orthogonal to each other) in each of the other two 16-cells. (Completely orthogonal great circles are Clifford parallel, but not all Clifford parallels are orthogonal.[lower-alpha 44]) A 60 degree isoclinic rotation of the 24-cell in hexagonal invariant planes takes each square great circle to a Clifford parallel (but non-orthogonal) square great circle in a different 16-cell.
- ↑ Jump up to: 44.0 44.1 Each square plane is isoclinic (Clifford parallel) to five other square planes but completely orthogonal[lower-alpha 7] to only one of them.[lower-alpha 43] Every pair of completely orthogonal planes has Clifford parallel great circles, but not all Clifford parallel great circles are orthogonal (e.g., none of the hexagonal geodesics in the 24-cell are mutually orthogonal).
- ↑ Jump up to: 45.0 45.1 45.2 In 4-space, two great circles can be perpendicular and share a common center which is their only point of intersection, because there is more than one great 2-sphere on the 3-sphere. The dimensionally analogous structure to a great circle (a great 1-sphere) is a great 2-sphere,[16] which is an ordinary sphere that constitutes an equator boundary dividing the 3-sphere into two equal halves, just as a great circle divides the 2-sphere. Although two Clifford parallel great circles[lower-alpha 35] occupy the same 3-sphere, they lie on different great 2-spheres. The great 2-spheres are Clifford parallel 3-dimensional objects, displaced relative to each other by a fixed distance d in the fourth dimension. Their corresponding points (on their two surfaces) are d apart. The 2-spheres (by which we mean their surfaces) do not intersect at all, although they have a common center point in 4-space. The displacement d between a pair of their corresponding points is the chord of a great circle which intersects both 2-spheres, so d can be represented equivalently as a linear chordal distance, or as an angular distance.
- ↑ Jump up to: 46.0 46.1 46.2 46.3 The 24-cell has three sets of 6 non-intersecting Clifford parallel great circles each passing through 4 vertices (a great square), with only one great square in each set passing through each vertex, and the 6 squares in each set reaching all 24 vertices.[lower-alpha 12] Each set constitutes a discrete Hopf fibration of 6 interlocking great squares, which is simply the compound of the three inscribed 16-cell's discrete Hopf fibrations of 2 interlocking great squares. The 24-cell can also be divided (six different ways) into 3 disjoint subsets of 8 vertices (octagrams) that do not lie in a square central plane, but comprise a 16-cell and lie on a skew octagram3 forming an isoclinic geodesic or isocline that is the rotational cirle traversed by those 8 vertices in one particular left or right isoclinic rotation as they rotate positions within the 16-cell.
- ↑ The sum of 1・96 + 2・72 + 3・96 + 4・12 is 576.
- ↑ The sum of the squared lengths of all the distinct chords of any regular convex n-polytope of unit radius is the square of the number of vertices.[17]
- ↑ Jump up to: 49.00 49.01 49.02 49.03 49.04 49.05 49.06 49.07 49.08 49.09 49.10 A point under isoclinic rotation traverses the diagonal[lower-alpha 15] straight line of a single isoclinic geodesic, reaching its destination directly, instead of the bent line of two successive simple geodesics.[lower-alpha 83] A geodesic is the shortest path through a space (intuitively, a string pulled taught between two points). Simple geodesics are great circles lying in a central plane (the only kind of geodesics that occur in 3-space on the 2-sphere). Isoclinic geodesics are different: they do not lie in a single plane; they are 4-dimensional spirals rather than simple 2-dimensional circles.[lower-alpha 81] But they are not like 3-dimensional screw threads either, because they form a closed loop like any circle.[lower-alpha 101] Isoclinic geodesics are 4-dimensional great circles, and they are just as circular as 2-dimensional circles: in fact, twice as circular, because they curve in two orthogonal great circles at once.[lower-alpha 102] They are true circles,[lower-alpha 82] and even form fibrations like ordinary 2-dimensional great circles.[lower-alpha 40][lower-alpha 46] These isoclines are geodesic 1-dimensional lines embedded in a 4-dimensional space. On the 3-sphere[lower-alpha 103] they always occur in pairs[lower-alpha 105] as Villarceau circles on the Clifford torus, the geodesic paths traversed by vertices in an isoclinic rotation. They are helices bent into a Möbius loop in the fourth dimension, taking a diagonal winding route around the 3-sphere through the non-adjacent vertices[lower-alpha 21] of a 4-polytope's skew Clifford polygon.[lower-alpha 87]
- ↑ Each pair of parallel √1 edges joins a pair of parallel √3 chords to form one of 48 rectangles (inscribed in the 16 central hexagons), and each pair of parallel √2 chords joins another pair of parallel √2 chords to form one of the 18 central squares.
- ↑ Jump up to: 51.0 51.1 51.2 51.3 One way to visualize the n-dimensional hyperplanes is as the n-spaces which can be defined by n + 1 points. A point is the 0-space which is defined by 1 point. A line is the 1-space which is defined by 2 points which are not coincident. A plane is the 2-space which is defined by 3 points which are not colinear (any triangle). In 4-space, a 3-dimensional hyperplane is the 3-space which is defined by 4 points which are not coplanar (any tetrahedron). In 5-space, a 4-dimensional hyperplane is the 4-space which is defined by 5 points which are not cocellular (any 5-cell). These simplex figures divide the hyperplane into two parts (inside and outside the figure), but in addition they divide the enclosing space into two parts (above and below the hyperplane). The n points bound a finite simplex figure (from the outside), and they define an infinite hyperplane (from the inside).[34] These two divisions are orthogonal, so the defining simplex divides space into six regions: inside the simplex and in the hyperplane, inside the simplex but above or below the hyperplane, outside the simplex but in the hyperplane, and outside the simplex above or below the hyperplane.
- ↑ Jump up to: 52.0 52.1 52.2 52.3 52.4 Two angles are required to fix the relative positions of two planes in 4-space.[18] Since all planes in the same hyperplane[lower-alpha 51] are 0 degrees apart in one of the two angles, only one angle is required in 3-space. Great hexagons in different hyperplanes are 60 degrees apart in both angles. Great squares in different hyperplanes are 90 degrees apart in both angles (completely orthogonal)[lower-alpha 7] or 60 degrees apart in both angles.[lower-alpha 43] Planes which are separated by two equal angles are called isoclinic. Planes which are isoclinic have Clifford parallel great circles.[lower-alpha 35] A great square and a great hexagon in different hyperplanes may be isoclinic, but often they are separated by a 90 degree angle and a 60 degree angle.
- ↑ Each pair of Clifford parallel polygons lies in two different hyperplanes (cuboctahedrons). The 4 Clifford parallel hexagons lie in 4 different cuboctahedrons.
- ↑ Two intersecting great squares or great hexagons share two opposing vertices, but squares or hexagons on Clifford parallel great circles share no vertices. Two intersecting great triangles share only one vertex, since they lack opposing vertices.
- ↑ Jump up to: 55.0 55.1 55.2 55.3 In the 24-cell each great square plane is completely orthogonal[lower-alpha 7] to another great square plane, and each great hexagon plane is completely orthogonal to a plane which intersects only two antipodal vertices: a great digon plane.
- ↑ The 600-cell is larger than the 24-cell, and contains the 24-cell as an interior feature.[19] The regular 5-cell is not found in the interior of any convex regular 4-polytope except the 120-cell,[20] though every convex 4-polytope can be deconstructed into irregular 5-cells.
- ↑ This animation shows the construction of a rhombic dodecahedron from a cube, by inverting the center-to-face pyramids of a cube. Gosset's construction of a 24-cell from a tesseract is the 4-dimensional analogue of this process, inverting the center-to-cell pyramids of an 8-cell (tesseract).[22]
 Construction of a rhombic dodecahedron from a cube.
Construction of a rhombic dodecahedron from a cube. - ↑ We can cut a vertex off a polygon with a 0-dimensional cutting instrument (like the point of a knife, or the head of a zipper) by sweeping it along a 1-dimensional line, exposing a new edge. We can cut a vertex off a polyhedron with a 1-dimensional cutting edge (like a knife) by sweeping it through a 2-dimensional face plane, exposing a new face. We can cut a vertex off a polychoron (a 4-polytope) with a 2-dimensional cutting plane (like a snowplow), by sweeping it through a 3-dimensional cell volume, exposing a new cell. Notice that as within the new edge length of the polygon or the new face area of the polyhedron, every point within the new cell volume is now exposed on the surface of the polychoron.
- ↑ Each cell face plane intersects with the other face planes of its kind to which it is not completely orthogonal or parallel at their characteristic vertex chord edge. Adjacent face planes of orthogonally-faced cells (such as cubes) intersect at an edge since they are not completely orthogonal.[lower-alpha 11] Although their dihedral angle is 90 degrees in the boundary 3-space, they lie in the same hyperplane[lower-alpha 51] (they are coincident rather than perpendicular in the fourth dimension); thus they intersect in a line, as non-parallel planes do in any 3-space.
- ↑ Jump up to: 60.0 60.1 The only planes through exactly 6 vertices of the 24-cell (not counting the central vertex) are the 16 hexagonal great circles. There are no planes through exactly 5 vertices. There are several kinds of planes through exactly 4 vertices: the 18 √2 square great circles, the 72 √1 square (tesseract) faces, and 144 √1 by √2 rectangles. The planes through exactly 3 vertices are the 96 √2 equilateral triangle (16-cell) faces, and the 96 √1 equilateral triangle (24-cell) faces. There are an infinite number of central planes through exactly two vertices (great circle digons); 16 are distinguished, as each is completely orthogonal[lower-alpha 7] to one of the 16 hexagonal great circles. Only the polygons composed of 24-cell √1 edges are visible in the projections and rotating animations illustrating this article; the others contain invisible interior chords.[lower-alpha 32]
- ↑ The 24-cell's cubical vertex figure[lower-alpha 38] has been truncated to a tetrahedral vertex figure (see Kepler's drawing). The vertex cube has vanished, and now there are only 4 corners of the vertex figure where before there were 8. Four tesseract edges converge from the tetrahedron vertices and meet at its center, where they do not cross (since the tetrahedron does not have opposing vertices).
- ↑ Jump up to: 62.0 62.1 62.2 Two tesseracts share only vertices, not any edges, faces, cubes (with inscribed tetrahedra), or octahedra (whose central square planes are square faces of cubes). An octahedron that touches another octahedron at a vertex (but not at an edge or a face) is touching an octahedron in another tesseract, and a pair of adjacent cubes in the other tesseract whose common square face the octahedron spans, and a tetrahedron inscribed in each of those cubes.
- ↑ Jump up to: 63.0 63.1 63.2 63.3 The common core of the 24-cell and its inscribed 8-cells and 16-cells is the unit-radius 24-cell's insphere-inscribed dual 24-cell of edge length and radius 1/2.[26] Rectifying any of the three 16-cells reveals this smaller 24-cell, which has a 4-content of only 1/8 (1/16 that of the unit-radius 24-cell). Its vertices lie at the centers of the 24-cell's octahedral cells, which are also the centers of the tesseracts' square faces, and are also the centers of the 16-cells' edges.[27]
- ↑ The 24-cell's cubical vertex figure[lower-alpha 38] has been truncated to an octahedral vertex figure. The vertex cube has vanished, and now there are only 6 corners of the vertex figure where before there were 8. The 6 √2 chords which formerly converged from cube face centers now converge from octahedron vertices; but just as before, they meet at the center where 3 straight lines cross perpendicularly. The octahedron vertices are located 90° away outside the vanished cube, at the new nearest vertices; before truncation those were 24-cell vertices in the second shell of surrounding vertices.
- ↑ Jump up to: 65.0 65.1 65.2 65.3 Each of the 72 √2 chords in the 24-cell is a face diagonal in two distinct cubical cells (of different 8-cells) and an edge of four tetrahedral cells (in just one 16-cell).
- ↑ Jump up to: 66.0 66.1 An orthoscheme is a chiral irregular simplex with right triangle faces that is characteristic of some polytope if it will exactly fill that polytope with the reflections of itself in its own facets (its mirror walls). Every regular polytope can be dissected radially into instances of its characteristic orthoscheme surrounding its center. The characteristic orthoscheme has the shape described by the same Coxeter-Dynkin diagram as the regular polytope without the generating point ring.
- ↑ The 24 vertices of the 24-cell, each used twice, are the vertices of three 16-vertex tesseracts.
- ↑ The 24 vertices of the 24-cell, each used once, are the vertices of three 8-vertex 16-cells.[lower-alpha 16]
- ↑ The edges of the 16-cells are not shown in any of the renderings in this article; if we wanted to show interior edges, they could be drawn as dashed lines. The edges of the inscribed tesseracts are always visible, because they are also edges of the 24-cell.
- ↑ The 4-dimensional content of the unit edge length tesseract is 1 (by definition). The content of the unit edge length 24-cell is 2, so half its content is inside each tesseract, and half is between their envelopes. Each 16-cell (edge length √2) encloses a content of 2/3, leaving 1/3 of an enclosing tesseract between their envelopes.
- ↑ Between the 24-cell envelope and the 8-cell envelope, we have the 8 cubic pyramids of Gosset's construction. Between the 8-cell envelope and the 16-cell envelope, we have 16 right tetrahedral pyramids, with their apexes filling the corners of the tesseract.
- ↑ Jump up to: 72.0 72.1 72.2 Consider the three perpendicular √2 long diameters of the octahedral cell.[31] Each of them is an edge of a different 16-cell. Two of them are the face diagonals of the square face between two cubes; each is a √2 chord that connects two vertices of those 8-cell cubes across a square face, connects two vertices of two 16-cell tetrahedra (inscribed in the cubes), and connects two opposite vertices of a 24-cell octahedron (diagonally across two of the three orthogonal square central sections).[lower-alpha 65] The third perpendicular long diameter of the octahedron does exactly the same (by symmetry); so it also connects two vertices of a pair of cubes across their common square face: but a different pair of cubes, from one of the other tesseracts in the 24-cell.[lower-alpha 62]
- ↑ Jump up to: 73.0 73.1 73.2 Because there are three overlapping tesseracts inscribed in the 24-cell,[lower-alpha 22] each octahedral cell lies on a cubic cell of one tesseract (in the cubic pyramid based on the cube, but not in the cube's volume), and in two cubic cells of each of the other two tesseracts (cubic cells which it spans, sharing their volume).[lower-alpha 72]
- ↑ This might appear at first to be angularly impossible, and indeed it would be in a flat space of only three dimensions. If two cubes rest face-to-face in an ordinary 3-dimensional space (e.g. on the surface of a table in an ordinary 3-dimensional room), an octahedron will fit inside them such that four of its six vertices are at the four corners of the square face between the two cubes; but then the other two octahedral vertices will not lie at a cube corner (they will fall within the volume of the two cubes, but not at a cube vertex). In four dimensions, this is no less true! The other two octahedral vertices do not lie at a corner of the adjacent face-bonded cube in the same tesseract. However, in the 24-cell there is not just one inscribed tesseract (of 8 cubes), there are three overlapping tesseracts (of 8 cubes each). The other two octahedral vertices do lie at the corner of a cube: but a cube in another (overlapping) tesseract.[lower-alpha 73]
- ↑ It is important to visualize the radii only as invisible interior features of the 24-cell (dashed lines), since they are not edges of the honeycomb. Similarly, the center of the 24-cell is empty (not a vertex of the honeycomb).
- ↑ Unlike the 24-cell and the tesseract, the 16-cell is not radially equilateral; therefore 16-cells of two different sizes (unit edge length versus unit radius) occur in the unit edge length honeycomb. The twenty-four 16-cells that meet at the center of each 24-cell have unit edge length, and radius √2/2. The three 16-cells inscribed in each 24-cell have edge length √2, and unit radius.
- ↑ Three dimensional rotations occur around an axis line. Four dimensional rotations may occur around a plane. So in three dimensions we may fold planes around a common line (as when folding a flat net of 6 squares up into a cube), and in four dimensions we may fold cells around a common plane (as when folding a flat net of 8 cubes up into a tesseract). Folding around a square face is just folding around two of its orthogonal edges at the same time; there is not enough space in three dimensions to do this, just as there is not enough space in two dimensions to fold around a line (only enough to fold around a point).
- ↑ There are (at least) two kinds of correct dimensional analogies: the usual kind between dimension n and dimension n + 1, and the much rarer and less obvious kind between dimension n and dimension n + 2. An example of the latter is that rotations in 4-space may take place around a single point, as do rotations in 2-space. Another is the n-sphere rule that the surface area of the sphere embedded in n+2 dimensions is exactly 2π r times the volume enclosed by the sphere embedded in n dimensions, the most well-known examples being that the circumference of a circle is 2π r times 1, and the surface area of the ordinary sphere is 2π r times 2r. Coxeter cites[42] this as an instance in which dimensional analogy can fail us as a method, but it is really our failure to recognize whether a one- or two-dimensional analogy is the appropriate method.
- ↑ Rotations in 4-dimensional Euclidean space may occur around a plane, as when adjacent cells are folded around their plane of intersection (by analogy to the way adjacent faces are folded around their line of intersection).[lower-alpha 77] But in four dimensions there is yet another way in which rotations can occur, called a double rotation. Double rotations are an emergent phenomenon in the fourth dimension and have no analogy in three dimensions: folding up square faces and folding up cubical cells are both examples of simple rotations, the only kind that occur in fewer than four dimensions. In 3-dimensional rotations, the points in a line remain fixed during the rotation, while every other point moves. In 4-dimensional simple rotations, the points in a plane remain fixed during the rotation, while every other point moves. In 4-dimensional double rotations, a point remains fixed during rotation, and every other point moves (as in a 2-dimensional rotation!).[lower-alpha 78]
- ↑ Jump up to: 80.0 80.1 80.2 80.3 80.4 In a Clifford displacement, also known as an isoclinic rotation, all the Clifford parallel[lower-alpha 35] invariant planes are displaced in four orthogonal directions at once: they are rotated by the same angle, and at the same time they are tilted sideways by that same angle in the completely orthogonal rotation.[lower-alpha 82] A Clifford displacement is 4-dimensionally diagonal.[lower-alpha 15] Every plane that is Clifford parallel to one of the completely orthogonal planes (including in this case an entire Clifford parallel bundle of 4 hexagons, but not all 16 hexagons) is invariant under the isoclinic rotation: all the points in the plane rotate in circles but remain in the plane, even as the whole plane tilts sideways.[lower-alpha 87] All 16 hexagons rotate by the same angle (though only 4 of them do so invariantly). All 16 hexagons are rotated by 60 degrees, and also displaced sideways by 60 degrees to a Clifford parallel hexagon. All of the other central polygons (e.g. squares) are also displaced to a Clifford parallel polygon 60 degrees away.
- ↑ Jump up to: 81.0 81.1 81.2 In a double rotation each vertex can be said to move along two completely orthogonal great circles at the same time, but it does not stay within the central plane of either of those original great circles; rather, it moves along a helical geodesic that traverses diagonally between great circles. The two completely orthogonal planes of rotation are said to be invariant because the points in each stay in their places in the plane as the plane moves, rotating and tilting sideways by the angle that the other plane rotates.
- ↑ Jump up to: 82.0 82.1 82.2 82.3 82.4 82.5 82.6 An isoclinic rotation by 60° is two simple rotations by 60° at the same time.[lower-alpha 100] It moves all the vertices 120° at the same time, in various different directions. Six successive diagonal rotational increments, of 60°x60° each, move each vertex through 720° on a Möbius double loop called an isocline, twice around the 24-cell and back to its point of origin, in the same time (six rotational units) that it would take a simple rotation to take the vertex once around the 24-cell on an ordinary great circle.[lower-alpha 101] The helical double loop 4𝝅 isocline is just another kind of single full circle, of the same time interval and period (6 chords) as the simple great circle. The isocline is one true circle,[lower-alpha 102] as perfectly round and geodesic as the simple great circle, even through its chords are √3 longer, its circumference is 4𝝅 instead of 2𝝅,[lower-alpha 104] it circles through four dimensions instead of two,[lower-alpha 105] and it acts in two chiral forms (left and right) even though all such circles of the same circumference are directly congruent.[lower-alpha 87] Nevertheless, to avoid confusion we always refer to it as an isocline and reserve the term great circle for an ordinary great circle in the plane.
- ↑ Jump up to: 83.0 83.1 83.2 83.3 83.4 Any double rotation (including an isoclinic rotation) can be seen as the composition of two simple rotations a and b: the left double rotation as a then b, and the right double rotation as b then a. Simple rotations are not commutative; left and right rotations (in general) reach different destinations. The difference between a double rotation and its two composing simple rotations is that the double rotation is 4-dimensionally diagonal: each moving vertex reaches its destination directly without passing through the intermediate point touched by a then b, or the other intermediate point touched by b then a, by rotating on a single helical geodesic (so it is the shortest path).[lower-alpha 81] Conversely, any simple rotation can be seen as the composition of two equal-angled double rotations (a left isoclinic rotation and a right isoclinic rotation),[lower-alpha 82] as discovered by Cayley; perhaps surprisingly, this composition is commutative, and is possible for any double rotation as well.[45]
- ↑ A rotation in 4-space is completely characterized by choosing an invariant plane and an angle and direction (left or right) through which it rotates, and another angle and direction through which its one completely orthogonal invariant plane rotates. Two rotational displacements are identical if they have the same pair of invariant planes of rotation, through the same angles in the same directions (and hence also the same chiral pairing of directions). Thus the general rotation in 4-space is a double rotation, characterized by two angles. A simple rotation is a special case in which one rotational angle is 0.[lower-alpha 83] An isoclinic rotation is a different special case, similar but not identical to two simple rotations through the same angle.[lower-alpha 80]
- ↑ Jump up to: 85.0 85.1 The adjectives left and right are commonly used in two different senses, to distinguish two distinct kinds of pairing. They can refer to alternate directions: the hand on the left side of the body, versus the hand on the right side. Or they can refer to a chiral pair of enantiamorphous objects: a left hand is the mirror image of a right hand (like an inside-out glove). In the case of hands the sense intended is rarely ambiguous, because of course the hand on your left side is the mirror image of the hand on your right side: a hand is either left or right in both senses. But in the case of double-rotating 4-dimensional objects, only one sense of left versus right properly applies: the enantiamorphous sense, in which the left and right rotation are inside-out mirror images of each other. There are two directions, which we may call positive and negative, in which moving vertices may be circling on their isoclines, but it would be ambiguous to label those circular directions "right" and "left", since a rotation's direction and its chirality are independent properties: a right (or left) rotation may be circling in either the positive or negative direction. The left rotation is not rotating "to the left", the right rotation is not rotating "to the right", and unlike your left and right hands, double rotations do not lie on the left or right side of the 4-polytope. If double rotations must be analogized to left and right hands, they are better thought of as a pair of clasped hands, centered on the body, because of course they have a common center.
- ↑ Jump up to: 86.0 86.1 86.2 The 24-cell's Petrie polygon is a skew dodecagon {12} and also (orthogonally) a skew dodecagram {12/5} which zig-zags 90° left and right like the edges dividing the black and white squares on the chessboard.[62] In contrast, the skew hexagram2 isocline does not zig-zag, and stays on one side or the other of the dividing line between black and white, like the bishops' paths along the diagonals of either the black or white squares of the chessboard.[lower-alpha 21] The Petrie dodecagon is a circular helix of √1 edges that zig-zag 90° left and right along 12 edges of 6 different octahedra (with 3 consecutive edges in each octahedron) in a 360° rotation. In contrast, the isoclinic hexagram2 has √3 edges which all bend either left or right at every second vertex along a geodesic spiral of both chiralities (left and right)[lower-alpha 87] but only one color (black or white),[lower-alpha 93] visiting one vertex of each of those same 6 octahedra in a 720° rotation.
- ↑ Jump up to: 87.00 87.01 87.02 87.03 87.04 87.05 87.06 87.07 87.08 87.09 87.10 87.11 87.12 The chord-path of an isocline (the geodesic along which a vertex moves under isoclinic rotation) may be called the 4-polytope's Clifford polygon, as it is the skew polygonal shape of the rotational circles traversed by the 4-polytope's vertices in its characteristic Clifford displacement.[61] The isocline is a helical Möbius double loop which reverses its chirality twice in the course of a full double circuit. The two loops are both entirely contained within the same cell ring, where they both follow chords connecting even (odd) vertices: typically opposite vertices of adjacent cells, two edge lengths apart.[lower-alpha 93] Both "halves" of the double loop pass through each cell in the cell ring, but intersect only two even (odd) vertices in each even (odd) cell. Each pair of intersected vertices in an even (odd) cell lie opposite each other on the Möbius strip, exactly one edge length apart. Thus each cell has both helices passing through it, which are Clifford parallels[lower-alpha 35] of opposite chirality at each pair of parallel points. Globally these two helices are a single connected circle of both chiralities, with no net torsion. An isocline acts as a left (or right) isocline when traversed by a left (or right) rotation (of different fibrations).[lower-alpha 82]
- ↑ That a double rotation can turn a 4-polytope inside out is even more noticeable in the tesseract double rotation.
- ↑ Since it is difficult to color points and lines white, we sometimes use black and red instead of black and white. In particular, isocline chords are sometimes shown as black or red dashed lines.[lower-alpha 32]
- ↑ Jump up to: 90.0 90.1 90.2 Each great square plane is isoclinic (Clifford parallel) to five other square planes but completely orthogonal[lower-alpha 7] to only one of them.[lower-alpha 43] Every pair of completely orthogonal planes has Clifford parallel great circles, but not all Clifford parallel great circles are orthogonal (e.g., none of the hexagonal geodesics in the 24-cell are mutually orthogonal). There is also another way in which completely orthogonal planes are in a distinguished category of Clifford parallel planes: they are not chiral, or strictly speaking they possess both chiralities. A pair of isoclinic (Clifford parallel) planes is either a left pair or a right pair, unless they are separated by two angles of 90° (completely orthogonal planes) or 0° (coincident planes).[55] Most isoclinic planes are brought together only by a left isoclinic rotation or a right isoclinic rotation, respectively. Completely orthogonal planes are special: the pair of planes is both a left and a right pair, so either a left or a right isoclinic rotation will bring them together. This occurs because isoclinic planes are 180° apart at all vertex pairs: not just Clifford parallel but completely orthogonal. The isoclines (chiral vertex paths)[lower-alpha 49] of 90° isoclinic rotations are special for the same reason. Left and right isoclines loop through the same set of antipodal vertices (hitting both ends of each 16-cell axis), instead of looping through disjoint left and right subsets of black or white antipodal vertices (hitting just one end of each axis), as the left and right isoclines of all other fibrations do.
- ↑ Chirality and even/odd parity are distinct flavors. Things which have even/odd coordinate parity are black or white: the squares of the chessboard,[lower-alpha 89] cells, vertices and the isoclines which connect them by isoclinic rotation.[lower-alpha 49] Everything else is black and white: e.g. adjacent face-bonded cell pairs, or edges and chords which are black at one end and white at the other. Things which have chirality come in right or left enantiomorphous forms: isoclinic rotations and chiral objects which include characteristic orthoschemes, pairs of Clifford parallel great polygon planes,[lower-alpha 90] fiber bundles of Clifford parallel circles (whether or not the circles themselves are chiral), and the chiral cell rings found in the 16-cell and 600-cell. Things which have neither an even/odd parity nor a chirality include all edges and faces (shared by black and white cells), great circle polygons and their fibrations, and non-chiral cell rings such as the 24-cell's cell rings of octahedra. Some things have both an even/odd parity and a chirality: isoclines are black or white because they connect vertices which are all of the same color, and they act as left or right chiral objects when they are vertex paths in a left or right rotation, although they have no inherent chirality themselves. Each left (or right) rotation traverses an equal number of black and white isoclines.[lower-alpha 87]
- ↑ Left and right isoclinic rotations partition the 24 cells (and 24 vertices) into black and white in the same way.[40] The rotations of all fibrations of the same kind of great polygon use the same chessboard, which is a convention of the coordinate system based on even and odd coordinates. Left and right are not colors: in either a left (or right) rotation half the moving vertices are black, running along black isoclines through black vertices, and the other half are white vertices, also rotating among themselves.[lower-alpha 91]
- ↑ Jump up to: 93.0 93.1 93.2 93.3 93.4 93.5 93.6 93.7 Isoclinic rotations[lower-alpha 49] partition the 24 cells (and the 24 vertices) of the 24-cell into two disjoint subsets of 12 cells (and 12 vertices), even and odd (or black and white), which shift places among themselves, in a manner dimensionally analogous to the way the bishops' diagonal moves[lower-alpha 21] restrict them to the black or white squares of the chessboard.[lower-alpha 92]
- ↑ Jump up to: 94.0 94.1 Although adjacent vertices on the isoclinic geodesic are a √3 chord apart, a point on a rigid body under rotation does not travel along a chord: it moves along an arc between the two endpoints of the chord (a longer distance). In a simple rotation between two vertices √3 apart, the vertex moves along the arc of a hexagonal great circle to a vertex two great hexagon edges away, and passes through the intervening hexagon vertex midway. But in an isoclinic rotation between two vertices √3 apart the vertex moves along a helical arc called an isocline (not a planar great circle),[lower-alpha 49] which does not pass through an intervening vertex: it misses the vertex nearest to its midpoint.[lower-alpha 21]
- ↑ P0 and P1 lie in the same hyperplane (the same central cuboctahedron) so their other angle of separation is 0.[lower-alpha 52]
- ↑ V0 and V2 are two √3 chords apart on the geodesic path of this rotational isocline, but that is not the shortest geodesic path between them. In the 24-cell, it is impossible for two vertices to be more distant than one √3 chord, unless they are antipodal vertices √4 apart.[lower-alpha 37] V0 and V2 are one √3 chord apart on some other isocline, and just √1 apart on some great hexagon. Between V0 and V2, the isoclinic rotation has gone the long way around the 24-cell over two √3 chords to reach a vertex that was only √1 away. More generally, isoclines are geodesics because the distance between their adjacent vertices is the shortest distance between those two vertices in some rotation connecting them, but on the 3-sphere there may be another rotation which is shorter. A path between two vertices along a geodesic is not always the shortest distance between them (even on ordinary great circle geodesics).
- ↑ P0 and P2 are 60° apart in both angles of separation.[lower-alpha 52] Clifford parallel planes are isoclinic (which means they are separated by two equal angles), and their corresponding vertices are all the same distance apart. Although V0 and V2 are two √3 chords apart[lower-alpha 96], P0 and P2 are just one √1 edge apart (at every pair of nearest vertices).
- ↑ Jump up to: 98.0 98.1 98.2 98.3 Each half of a skew hexagram is an open triangle of three √3 chords, the two open ends of which are one √1 edge length apart. The two halves, like the whole isocline, have no inherent chirality but the same parity-color (black or white). The halves are the two opposite "edges" of a Möbius strip that is √1 wide; it actually has only one edge, which is a single continuous circle with 6 chords.
- ↑ Jump up to: 99.0 99.1 99.2 Departing from any vertex V0 in the original great hexagon plane of isoclinic rotation P0, the first vertex reached V1 is 120 degrees away along a √3 chord lying in a different hexagonal plane P1. P1 is inclined to P0 at a 60° angle.[lower-alpha 95] The second vertex reached V2 is 120 degrees beyond V1 along a second √3 chord lying in another hexagonal plane P2 that is Clifford parallel to P0.[lower-alpha 97] (Notice that V1 lies in both intersecting planes P1 and P2, as V0 lies in both P0 and P1. But P0 and P2 have no vertices in common; they do not intersect.) The third vertex reached V3 is 120 degrees beyond V2 along a third √3 chord lying in another hexagonal plane P3 that is Clifford parallel to P1. V0 and V3 are adjacent vertices, √1 apart.[lower-alpha 98] The three √3 chords lie in different 8-cells.[lower-alpha 22] V0 to V3 is a 360° isoclinic rotation, and one half of the 24-cell's double-loop hexagram2 Clifford polygon.[lower-alpha 87]
- ↑ The composition of two simple 60° rotations in a pair of completely orthogonal invariant planes is a 60° isoclinic rotation in four pairs of completely orthogonal invariant planes.[lower-alpha 83] Thus the isoclinic rotation is the compound of four simple rotations, and all 24 vertices rotate in invariant hexagon planes, versus just 6 vertices in a simple rotation.
- ↑ Jump up to: 101.0 101.1 101.2 101.3 Because the 24-cell's helical hexagram2 geodesic is bent into a twisted ring in the fourth dimension like a Möbius strip, its screw thread doubles back across itself in each revolution, reversing its chirality[lower-alpha 87] but without ever changing its even/odd parity of rotation (black or white).[lower-alpha 93] The 6-vertex isoclinic path forms a Möbius double loop, like a 3-dimensional double helix with the ends of its two parallel 3-vertex helices cross-connected to each other. This 60° isocline[lower-alpha 108] is a skewed instance of the regular compound polygon denoted {6/2}=2{3} or hexagram2.[lower-alpha 98] Successive √3 edges belong to different 8-cells, as the 720° isoclinic rotation takes each hexagon through all six hexagons in the 6-cell ring, and each 8-cell through all three 8-cells twice.[lower-alpha 22]
- ↑ Jump up to: 102.0 102.1 Isoclinic geodesics or isoclines are 4-dimensional great circles in the sense that they are 1-dimensional geodesic lines that curve in 4-space in two orthogonal great circles at once.[lower-alpha 103] They should not be confused with great 2-spheres,[16] which are the 4-dimensional analogues of great circles (great 1-spheres).[lower-alpha 45] Discrete isoclines are polygons;[lower-alpha 87] discrete great 2-spheres are polyhedra.
- ↑ Jump up to: 103.0 103.1 103.2 103.3 All isoclines are geodesics, and isoclines on the 3-sphere are circles (curving equally in each dimension), but not all isoclines on 3-manifolds in 4-space are circles.
- ↑ All 3-sphere isoclines of the same circumference are directly congruent circles.[lower-alpha 103] An ordinary great circle is an isocline of circumference 2𝝅; simple rotations take place on 2𝝅 isoclines. Double rotations may have isoclines of up to 8𝝅 circumference. Because the characteristic rotations of several regular 4-polytopes take place in the same invariant planes (the 24-cell's hexagonal planes), those rotations all have congruent isoclines of 4𝝅 circumference. The regular 4-polytopes which rotate on 4𝝅 isoclines characteristically (when they are rotating in the isoclinic invariant planes containing their edges) are the 5-cell, the 8-cell, the 24-cell and the 120-cell.
- ↑ Jump up to: 105.0 105.1 105.2 Isoclines on the 3-sphere occur in non-intersecting pairs of even/odd coordinate parity.[lower-alpha 93] A single black or white isocline forms a Möbius loop called the {1,1} torus knot or Villarceau circle[53] in which each of two "circles" linked in a Möbius "figure eight" loop traverses through all four dimensions.[lower-alpha 87] The double loop is a true circle in four dimensions.[lower-alpha 82] Even and odd isoclines are also linked, not in a Möbius loop but as a Hopf link of two non-intersecting circles,[lower-alpha 35] as are all the Clifford parallel isoclines of a Hopf fiber bundle.
- ↑ In a 720° isoclinic rotation of a rigid 24-cell the 24 vertices rotate along four separate Clifford parallel hexagram2 geodesic loops (six vertices circling in each loop) and return to their original positions.[lower-alpha 105]
- ↑ The length of a strip can be measured at its centerline, or by cutting the resulting Möbius strip perpendicularly to its boundary so that it forms a rectangle.
- ↑ A strip of paper can form a flattened Möbius strip in the plane by folding it at [math]\displaystyle{ 60^\circ }[/math] angles so that its center line lies along an equilateral triangle, and attaching the ends. The shortest strip for which this is possible consists of three equilateral paper triangles, folded at the edges where two triangles meet. Since the loop traverses both sides of each paper triangle, it is a hexagonal loop over six equilateral triangles. Its aspect ratio – the ratio of the strip's length[lower-alpha 107] to its width – is [math]\displaystyle{ \sqrt 3\approx 1.73 }[/math].
- ↑ Each set of Clifford parallel great circle polygons is a different bundle of fibers than the corresponding set of Clifford parallel isocline[lower-alpha 49] polygrams, but the two fiber bundles together constitute the same discrete Hopf fibration, because they enumerate the 24 vertices together by their intersection in the same distinct (left or right) isoclinic rotation. They are the warp and woof of the same woven fabric that is the fibration.
- ↑ Jump up to: 110.0 110.1 110.2 The choice of a partitioning of a regular 4-polytope into cell rings (a fibration) is arbitrary, because all of its cells are identical. No particular fibration is distinguished, unless the 4-polytope is rotating. Each fibration corresponds to a left-right pair of isoclinic rotations in a particular set of Clifford parallel invariant central planes of rotation. In the 24-cell, distinguishing a hexagonal fibration[lower-alpha 40] means choosing a cell-disjoint set of four 6-cell rings that is the unique container of a left-right pair of isoclinic rotations in four Clifford parallel hexagonal invariant planes. The left and right rotations take place in chiral subspaces of that container,[60] but the fibration and the octahedral cell rings themselves are not chiral objects.[lower-alpha 118]
- ↑ All isoclinic planes are Clifford parallels (completely disjoint).[lower-alpha 25] Three and four dimensional cocentric objects may intersect (sharing elements) but still be related by an isoclinic rotation. Polyhedra and 4-polytopes may be isoclinic and not disjoint, if all of their corresponding planes are either Clifford parallel, or cocellular (in the same hyperplane) or coincident (the same plane).
- ↑ By generate we mean simply that some vertex of the first polytope will visit each vertex of the generated polytope in the course of the rotation.
- ↑ Like a key operating a four-dimensional lock, an object must twist in two completely perpendicular tumbler cylinders in order to move the short distance between Clifford parallel subspaces.
- ↑ Just as each face of a polyhedron occupies a different (2-dimensional) face plane, each cell of a polychoron occupies a different (3-dimensional) cell hyperplane.[lower-alpha 51]
- ↑ Jump up to: 115.0 115.1 There is a choice of planes in which to fold the column into a ring, but they are equivalent in that they produce congruent rings. Whichever folding planes are chosen, each of the six helices joins its own two ends and forms a simple great circle hexagon. These hexagons are not helices: they lie on ordinary flat great circles. Three of them are Clifford parallel[lower-alpha 35] and belong to one hexagonal fibration. They intersect the other three, which belong to another hexagonal fibration. The three parallel great circles of each fibration spiral around each other in the sense that they form a link of three ordinary circles, but they are not twisted: the 6-cell ring has no torsion, either clockwise or counterclockwise.[lower-alpha 118]
- ↑ When unit-edge octahedra are placed face-to-face the distance between their centers of volume is √2/3 ≈ 0.816.[58] When 24 face-bonded octahedra are bent into a 24-cell lying on the 3-sphere, the centers of the octahedra are closer together in 4-space. Within the curved 3-dimensional surface space filled by the 24 cells, the cell centers are still √2/3 apart along the curved geodesics that join them. But on the straight chords that join them, which dip inside the 3-sphere, they are only 1/2 edge length apart.
- ↑ The axial hexagon of the 6-octahedron ring does not intersect any vertices or edges of the 24-cell, but it does hit faces. In a unit-edge-length 24-cell, it has edges of length 1/2.[lower-alpha 116] Because it joins six cell centers, the axial hexagon is a great hexagon of the smaller dual 24-cell that is formed by joining the 24 cell centers.[lower-alpha 63]
- ↑ Jump up to: 118.0 118.1 118.2 118.3 118.4 Only one kind of 6-cell ring exists, not two different chiral kinds (right-handed and left-handed), because octahedra have opposing faces and form untwisted cell rings. In addition to two sets of three Clifford parallel[lower-alpha 35] great hexagons, three black and three white isoclinic hexagram geodesics run through the 6-cell ring.[lower-alpha 40] Each of these chiral skew hexagrams lies on a different kind of circle called an isocline,[lower-alpha 103] a helical circle winding through all four dimensions instead of lying in a single plane.[lower-alpha 49] These helical great circles occur in Clifford parallel fiber bundles just as ordinary planar great circles do. In the 6-cell ring, black and white hexagrams pass through even and odd vertices respectively, and miss the vertices in between, so the isoclines are disjoint.[lower-alpha 93]
- ↑ The three great hexagons are Clifford parallel, which is different than ordinary parallelism.[lower-alpha 35] Clifford parallel great hexagons pass through each other like adjacent links of a chain, forming a Hopf link. Unlike links in a 3-dimensional chain, they share the same center point. In the 24-cell, Clifford parallel great hexagons occur in sets of four, not three. The fourth parallel hexagon lies completely outside the 6-cell ring; its 6 vertices are completely disjoint from the ring's 18 vertices.
- ↑ In the column of 6 octahedral cells, we number the cells 0-5 going up the column. We also label each vertex with an integer 0-5 based on how many edge lengths it is up the column.
- ↑ An isoclinic rotation by a multiple of 60° takes even-numbered octahedra in the ring to even-numbered octahedra, and odd-numbered octahedra to odd-numbered octahedra.[lower-alpha 120] It is impossible for an even-numbered octahedron to reach an odd-numbered octahedron, or vice versa, by a left or a right isoclinic rotation alone.[lower-alpha 93]
- ↑ Two central planes in which the path bends 60° at the vertex are (a) the great hexagon plane that the chord before the vertex belongs to, and (b) the great hexagon plane that the chord after the vertex belongs to. Plane (b) contains the 120° isocline chord joining the original vertex to a vertex in great hexagon plane (c), Clifford parallel to (a); the vertex moves over this chord to this next vertex. The angle of inclination between the Clifford parallel (isoclinic) great hexagon planes (a) and (c) is also 60°. In this 60° interval of the isoclinic rotation, great hexagon plane (a) rotates 60° within itself and tilts 60° in an orthogonal plane (not plane (b)) to become great hexagon plane (c). The three great hexagon planes (a), (b) and (c) are not orthogonal (they ae inclined at 60° to each other), but (a) and (b) are two central hexagons in the same cuboctahedron, and (b) and (c) likewise in an orthogonal cuboctahedron.[lower-alpha 19]
- ↑ Each vertex of the 6-cell ring is intersected by two skew hexagrams of the same parity (black or white) belonging to different fibrations.[lower-alpha 118]
- ↑ Jump up to: 124.0 124.1 Each vertex of a 6-cell ring is missed by the two halves of the same Möbius double loop hexagram[lower-alpha 125], which curve past it on either side.
- ↑ Jump up to: 125.0 125.1 125.2 At each vertex there is only one adjacent great hexagon plane that the isocline can bend 60 degrees into: the isoclinic path is deterministic in the sense that it is linear, not branching, because each vertex in the cell ring is a place where just two of the six great hexagons contained in the cell ring cross. If each great hexagon is given edges and chords of a particular color (as in the 6-cell ring illustration), we can name each great hexagon by its color, and each kind of vertex by a hyphenated two-color name. The cell ring contains 18 vertices named by the 9 unique two-color combinations; each vertex and its antipodal vertex have the same two colors in their name, since when two great hexagons intersect they do so at antipodal vertices. Each isoclinic skew hexagram[lower-alpha 98] contains one √3 chord of each color, and visits 6 of the 9 different color-pairs of vertex.[lower-alpha 123] Each 6-cell ring contains six such isoclinic skew hexagrams, three black and three white.[lower-alpha 124]
- ↑ The √3 chord passes through the mid-edge of one of the 24-cell's √1 radii. Since the 24-cell can be constructed, with its long radii, from √1 triangles which meet at its center,[lower-alpha 2] this is a mid-edge of one of the six √1 triangles in a great hexagon, as seen in the chord diagram.
- ↑ Each pair of adjacent edges of a great hexagon has just one isocline curving alongside it,[lower-alpha 124] missing the vertex between the two edges (but not the way the √3 edge of the great triangle inscribed in the great hexagon misses the vertex,[lower-alpha 126] because the isocline is an arc on the surface not a chord). If we number the vertices around the hexagon 0-5, the hexagon has three pairs of adjacent edges connecting even vertices (one inscribed great triangle), and three pairs connecting odd vertices (the other inscribed great triangle). Even and odd pairs of edges have the arc of a black and a white isocline respectively curving alongside.[lower-alpha 93] The three black and three white isoclines belong to the same 6-cell ring of the same fibration.[lower-alpha 125]
- ↑ Jump up to: 128.0 128.1 Each hexagram isocline hits only one end of an axis, unlike a great circle which hits both ends. Clifford parallel pairs of black and white isoclines from the same left-right pair of isoclinic rotations (the same fibration) do not intersect, but they hit opposite (antipodal) vertices of one of the 24-cell's 12 axes.
- ↑ The isoclines themselves are not left or right, only the bundles are. Each isocline is left and right.[lower-alpha 87]
- ↑ The 12 black-white pairs of hexagram isoclines in each fibration[lower-alpha 128] and the 16 distinct hexagram isoclines in the 24-cell form a Reye configuration 124163, just the way the 24-cell's 12 axes and 16 hexagons do. Each of the 12 black-white pairs occurs in one cell ring of each fibration of 4 hexagram isoclines, and each cell ring contains 3 black-white pairs of the 16 hexagram isoclines.
- ↑ Jump up to: 131.0 131.1 As in the 16-cell, the isocline is an octagram which intersects only 8 vertices, even though the 24-cell has more vertices closer together than the 16-cell. The isocline curve misses the additional vertices in between. As in the 16-cell, where it misses the nearest vertices √2 away, the first vertex it intersects is the antipodal vertex. The 24-cell employs more octagram isoclines (3 in each rotation) than the 16-cell does (1 in each rotation). The 3 helical isoclines are Clifford parallel;[lower-alpha 35] they spiral around each other in a triple helix, with the disjoint helices' corresponding vertex pairs joined by √4 chords. The edges of the 3 octagram helices are also √4 chords; the entire triple helix of 3 isoclines consists of 96 √4 edges and 24 vertices, and is isomorphic to the entire 24-cell.
- ↑ The 600-cell's isoclinic rotation in great square planes takes whole 16-cells to other 16-cells in different 24-cells.
- ↑ Jump up to: 133.0 133.1 (Coxeter 1973) uses the greek letter 𝝓 (phi) to represent one of the three characteristic angles 𝟀, 𝝓, 𝟁 of a regular polytope. Because 𝝓 is commonly used to represent the golden ratio constant ≈ 1.618, for which Coxeter uses 𝝉 (tau), we reverse Coxeter's conventions, and use 𝝉 to represent the characteristic angle.
- ↑ For a regular k-polytope, the Coxeter-Dynkin diagram of the characteristic k-orthoscheme is the k-polytope's diagram without the generating point ring. The regular k-polytope is subdivided by its symmetry (k-1)-elements into g instances of its characteristic k-orthoscheme that surround its center, where g is the order of the k-polytope's symmetry group.[68]
- ↑ The four edges of each 4-orthoscheme which meet at the center of the regular 4-polytope are of unequal length, because they are the four characteristic radii of the regular 4-polytope: a vertex radius, an edge center radius, a face center radius, and a cell center radius. The five vertices of the 4-orthoscheme always include one regular 4-polytope vertex, one regular 4-polytope edge center, one regular 4-polytope face center, one regular 4-polytope cell center, and the regular 4-polytope center. Those five vertices (in that order) comprise a path along four mutually perpendicular edges (that makes three right angle turns), the characteristic feature of a 4-orthoscheme. The 4-orthoscheme has five dissimilar 3-orthoscheme facets.
- ↑ The reflecting surface of a (3-dimensional) polyhedron consists of 2-dimensional faces; the reflecting surface of a (4-dimensional) polychoron consists of 3-dimensional cells.
- ↑ Cayley showed that any rotation in 4-space can be decomposed into two isoclinic rotations,[lower-alpha 83] which intuitively we might see follows from the fact that any transformation from one inertial reference frame to another is expressable as a rotation in 4-dimensional Euclidean space.
- ↑ Jump up to: 138.0 138.1 Let Q denote a rotation, R a reflection, T a translation, and let Qq Rr T denote a product of several such transformations, all commutative with one another. Then RT is a glide-reflection (in two or three dimensions), QR is a rotary-reflection, QT is a screw-displacement, and Q2 is a double rotation (in four dimensions). Every orthogonal transformation is expressible as
Qq Rr
where 2q + r ≤ n, the number of dimensions. Transformations involving a translation are expressible as
Qq Rr T
where 2q + r + 1 ≤ n.
For n = 4 in particular, every displacement is either a double rotation Q2, or a screw-displacement QT (where the rotation component Q is a simple rotation). [If we assume the Galilean principle of relativity, every displacement in 4-space can be viewed as either of those, because we can view any QT as a Q2 in a linearly moving (translating) reference frame. Therefore any transformation from one inertial reference frame to another is expressable as a Q2. By the same principle, we can view any QT or Q2 as an isoclinic (equi-angled) Q2 by appropriate choice of reference frame.[lower-alpha 137] That is to say, Coxeter's relation is a mathematical statement of the principle of relativity, on group-theoretic grounds.] Every enantiomorphous transformation in 4-space (reversing chirality) is a QRT.[71] - ↑ The left planes are Clifford parallel, and the right planes are Clifford parallel; each set of planes is a fibration. Each left plane is Clifford parallel to its corresponding right plane, but the two sets of planes are not all mutually Clifford parallel; they are different fibrations, except in table rows where the left and right planes are the same set.
- ↑ Jump up to: 140.0 140.1 The [math]\displaystyle{ \pm q7 }[/math] and [math]\displaystyle{ \pm q8 }[/math] sets of planes are not disjoint; the union of any two of these sets is a set of 6 planes.
- ↑ Jump up to: 141.0 141.1 141.2 141.3 A quaternion group [math]\displaystyle{ \pm{q_n} }[/math] corresponds to a distinct set of Clifford parallel great circle polygons, e.g. [math]\displaystyle{ q7 }[/math] corresponds to a set of four disjoint great hexagons.[lower-alpha 20] Note that [math]\displaystyle{ q_n }[/math] and [math]\displaystyle{ -{q_n} }[/math] generally are distinct sets.
- ↑ Jump up to: 142.0 142.1 A quaternion Cartesian coordinate designates a vertex joined to a top vertex by one instance of a distinct chord. The conventional top vertex of a unit radius 4-polytope in standard (vertex-up) orientation is [math]\displaystyle{ (0,0,1,0) }[/math], the Cartesian "north pole". Thus e.g. [math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] designates a √1 chord of 60° arc-length. Each such distinct chord is an edge of a distinct great circle polygon, in this example a great hexagon, intersecting the north and south poles. Great circle polygons occur in sets of Clifford parallel central planes, each set of disjoint great circles comprising a discrete Hopf fibration that intersects every vertex just once. One great circle polygon in each set intersects the north and south poles. This quaternion coordinate [math]\displaystyle{ (\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{2}) }[/math] is thus representative of the 4 disjoint great hexagons pictured, a quaternion group[lower-alpha 141] which comprise one distinct fibration of the [16] great hexagons (four fibrations of great hexagons) that occur in the 24-cell.[lower-alpha 20]
- ↑ Each hexagon rides on only three skew hexagram isoclines, not six, because opposite vertices of each hexagon ride on opposing rails of the same Clifford hexagram, in the same (not opposite) rotational direction.[lower-alpha 87]
- ↑ Jump up to: 144.0 144.1 In this orthogonal projection of the 24-point 24-cell to a {12/4}=4{3} dodecagram, each point represents two vertices, and each line represents multiple √3 chords. Each disjoint triangle can be seen as a skew {6/2} hexagram with √3 edges: two open skew triangles with their opposite ends connected in a Möbius loop with a circumference of 4𝝅. Those 4 disjoint skew hexagram 4𝝅 isoclines are the Clifford parallel circular vertex paths of the fibration's characteristic left (and right) isoclinic rotation.[lower-alpha 49] The 4 Clifford parallel great hexagons of the fibration[lower-alpha 20] are invariant planes of this rotation. The great hexagons rotate in incremental displacements of 120° (60° like wheels and 60° like coins flipping) as their vertices move along parallel helical isocline paths through successive Clifford parallel hexagon planes.[lower-alpha 143] Alternatively, the 4 triangles can be seen as 8 disjoint triangles: 4 pairs of Clifford parallel great triangles, where two opposing great triangles lie in the same great hexagon central plane, so a fibration of 4 Clifford parallel great hexagon planes is represented, as in the 4 left planes of this rotation class (table row).[lower-alpha 20] This illustrates that the 4 hexagram isoclines also correspond to a distinct fibration, in fact the same fibration as the 4 great hexagons.
- ↑ The edges and 8𝝅 characteristic rotations of the 16-cell lie in the great square central planes. Rotations of this type are an expression of the symmetry group [math]\displaystyle{ B 4 }[/math]. The edges and 4𝝅 characteristic rotations of the 24-cell lie in the great hexagon (great triangle) central planes. Rotations of this type are an expression of the [math]\displaystyle{ F 4 }[/math] symmetry group.
- ↑ Two great circle polygons either intersect in a common axis, or they are Clifford parallel (isoclinic) and share no vertices.[lower-alpha 52] Three great squares and four great hexagons intersect at each 24-cell vertex. Each great hexagon intersects 9 distinct great squares, 3 in each of its 3 axes, and lies Clifford parallel to the other 9 great squares. Each great square intersects 8 distinct great hexagons, 4 in each of its 2 axes, and lies Clifford parallel to the other 8 great hexagons.
- ↑ Jump up to: 147.0 147.1 147.2 This hybrid isoclinic rotation carries the two kinds of central planes to each other: great square planes characteristic of the 16-cell and great hexagon (great triangle) planes characteristic of the 24-cell.[lower-alpha 145] This is possible because some great hexagon planes lie Clifford parallel to some great square planes.[lower-alpha 146]
- ↑ The 24-cell has 18 great squares, in 3 disjoint sets of 6 mutually orthogonal great squares comprising a 16-cell.[lower-alpha 10] Within each 16-cell are 3 sets of 2 completely orthogonal great squares, so each great square is disjoint not only from all the great squares in the other two 16-cells, but also from one other great square in the same 16-cell. Each great square is disjoint from 13 others, and shares two vertices (an axis) with 4 others (in the same 16-cell).
- ↑ Because each great square is completely orthogonal to another great square, the quaternion groups [math]\displaystyle{ q1 }[/math] and [math]\displaystyle{ -{q1} }[/math] (for example) correspond to the same set of great square planes. That distinct set of 6 disjoint great squares [math]\displaystyle{ \pm q1 }[/math] has two names, used in the left (or right) rotational context, because it constitutes both a left and a right fibration of great squares.
- ↑ In this orthogonal projection of the 24-point 24-cell to a {12/3}=3{4} dodecagram, each point represents two vertices, and each line represents multiple √2 chords. Each disjoint square can be seen as a skew {8/3} octagram with √2 edges: two open skew squares with their opposite ends connected in a Möbius loop with a circumference of 8𝝅. Those 3 disjoint skew octagram isoclines are the circular vertex paths characteristic of an isoclinic rotation in great square planes, in which the 6 Clifford parallel great squares are invariant rotation planes. The great squares rotate 180° (90° like wheels and 90° like coins flipping) as each vertex exchanges places with its antipodal vertex. Each octagram isocline circles through the 8 vertices of a disjoint 16-cell. Alternatively, the 3 squares can be seen as a fibration of 6 Clifford parallel squares, as in the (left) planes of this rotation class (table row).[lower-alpha 12] This illustrates that the 3 octagram isoclines also correspond to a distinct fibration, in fact the same fibration as the 6 squares.
- ↑ A quaternion Cartesian coordinate designates a vertex joined to a top vertex by one instance of a distinct chord. The conventional top vertex of a unit radius 4-polytope in cell-first orientation is [math]\displaystyle{ (0,0,\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2}) }[/math]. Thus e.g. [math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math] designates a √2 chord of 90° arc-length. Each such distinct chord is an edge of a distinct great circle polygon, in this example a great square, intersecting the top vertex. Great circle polygons occur in sets of Clifford parallel central planes, each set of disjoint great circles comprising a discrete Hopf fibration that intersects every vertex just once. One great circle polygon in each set intersects the top vertex. This quaternion coordinate [math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math] is thus representative of the 6 disjoint great squares pictured, a quaternion group[lower-alpha 141] which comprise one distinct fibration of the [18] great squares (three fibrations of great squares) that occur in the 24-cell.[lower-alpha 12]
- ↑ The representative coordinate [math]\displaystyle{ (\tfrac{\sqrt{2}}{2},\tfrac{\sqrt{2}}{2},0,0) }[/math] is not a vertex of the unit-radius 24-cell in standard (vertex-up) orientation, it is the center of an octahedral cell. Some of the 24-cell's lines of symmetry (Coxeter's "reflecting circles") run through cell centers rather than through vertices, and quaternion group [math]\displaystyle{ q6 }[/math] corresponds to a set of those. However, [math]\displaystyle{ q6 }[/math] also corresponds to the set of great squares pictured, which lie orthogonal to those cells (completely disjoint from the cell).[lower-alpha 151]
- ↑ In this isoclinic rotation, all the [math]\displaystyle{ q7 }[/math] planes move together, remain Clifford parallel while moving, and carry all their points with them as they move: they are invariant planes. Because the [math]\displaystyle{ q7 }[/math] set of 4 central polygons is a fibration covering all the vertices, every vertex is a point carried along in an invariant plane.
- ↑ A right rotation is performed by rotating the left and right planes in the "same" direction, and a left rotation is performed by rotating left and right planes in "opposite" directions, according to the right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes. Left and right rotations are chiral enantiamorphous shapes (like a pair of shoes), not opposite rotational directions. Both left and right rotations can be performed in either the positive or negative rotational direction (from left planes to right planes, or right planes to left planes), but that is an additional distinction.
Citations
- ↑ Coxeter 1973, p. 118, Chapter VII: Ordinary Polytopes in Higher Space.
- ↑ Johnson 2018, p. 249, 11.5.
- ↑ Ghyka 1977, p. 68.
- ↑ Coxeter 1973, p. 289, Epilogue; "Another peculiarity of four-dimensional space is the occurrence of the 24-cell {3,4,3}, which stands quite alone, having no analogue above or below."
- ↑ Coxeter 1995, p. 25, (Paper 3) Two aspects of the regular 24-cell in four dimensions.
- ↑ Coxeter 1968, p. 70, §4.12 The Classification of Zonohedra.
- ↑ Jump up to: 7.0 7.1 Coxeter 1973, pp. 292-293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions; An invaluable table providing all 20 metrics of each 4-polytope in edge length units. They must be algebraically converted to compare polytopes of unit radius.
- ↑ Coxeter 1973, p. 302, Table VI (ii): 𝐈𝐈 = {3,4,3}: see Result column
- ↑ Coxeter 1973, p. 156, §8.7. Cartesian Coordinates.
- ↑ Coxeter 1973, pp. 145-146, §8.1 The simple truncations of the general regular polytope.
- ↑ Waegell & Aravind 2009, pp. 4-5, §3.4 The 24-cell: points, lines and Reye’s configuration; In the 24-cell Reye's "points" and "lines" are axes and hexagons, respectively.
- ↑ Coxeter 1973, p. 298, Table V: The Distribution of Vertices of Four-Dimensional Polytopes in Parallel Solid Sections (§13.1); (i) Sections of {3,4,3} (edge 2) beginning with a vertex; see column a.
- ↑ Stillwell 2001, p. 17.
- ↑ Tyrrell & Semple 1971, pp. 5-6, §3. Clifford's original definition of parallelism.
- ↑ Kim & Rote 2016, pp. 8-10, Relations to Clifford Parallelism.
- ↑ Jump up to: 16.0 16.1 Stillwell 2001, p. 24.
- ↑ Copher 2019, p. 6, §3.2 Theorem 3.4.
- ↑ Kim & Rote 2016, p. 7, §6 Angles between two Planes in 4-Space; "In four (and higher) dimensions, we need two angles to fix the relative position between two planes. (More generally, k angles are defined between k-dimensional subspaces.)".
- ↑ Coxeter 1973, p. 153, 8.5. Gosset's construction for {3,3,5}: "In fact, the vertices of {3,3,5}, each taken 5 times, are the vertices of 25 {3,4,3}'s."
- ↑ Coxeter 1973, p. 304, Table VI(iv) II={5,3,3}: Faceting {5,3,3}[120𝛼4]{3,3,5} of the 120-cell reveals 120 regular 5-cells.
- ↑ Egan 2021, animation of a rotating 24-cell: red half-integer vertices (tesseract), Template:Font colour and black integer vertices (16-cell).
- ↑ Jump up to: 22.0 22.1 22.2 Coxeter 1973, p. 150, Gosset.
- ↑ Coxeter 1973, p. 148, §8.2. Cesaro's construction for {3, 4, 3}..
- ↑ Coxeter 1973, p. 302, Table VI(ii) II={3,4,3}, Result column.
- ↑ Coxeter 1973, pp. 149-150, §8.22. see illustrations Fig. 8.2A and Fig 8.2B
- ↑ Coxeter 1995, p. 29, (Paper 3) Two aspects of the regular 24-cell in four dimensions; "The common content of the 4-cube and the 16-cell is a smaller {3,4,3} whose vertices are the permutations of [(±1/2, ±1/2, 0, 0)]".
- ↑ Coxeter 1973, p. 147, §8.1 The simple truncations of the general regular polytope; "At a point of contact, [elements of a regular polytope and elements of its dual in which it is inscribed in some manner] lie in completely orthogonal subspaces[lower-alpha 7] of the tangent hyperplane to the sphere [of reciprocation], so their only common point is the point of contact itself[lower-alpha 11].... In fact, the [various] radii 0𝑹, 1𝑹, 2𝑹, ... determine the polytopes ... whose vertices are the centers of elements 𝐈𝐈0, 𝐈𝐈1, 𝐈𝐈2, ... of the original polytope."
- ↑ Jump up to: 28.0 28.1 Kepler 1619, p. 181.
- ↑ van Ittersum 2020, pp. 73-79, §4.2.
- ↑ Coxeter 1973, p. 269, §14.32. "For instance, in the case of [math]\displaystyle{ \gamma_4[2\beta_4] }[/math]...."
- ↑ van Ittersum 2020, p. 79.
- ↑ Coxeter 1973, p. 150: "Thus the 24 cells of the {3, 4, 3} are dipyramids based on the 24 squares of the [math]\displaystyle{ \gamma_4 }[/math]. (Their centres are the mid-points of the 24 edges of the [math]\displaystyle{ \beta_4 }[/math].)"
- ↑ Coxeter 1973, p. 12, §1.8. Configurations.
- ↑ Coxeter 1973, p. 120, §7.2.: "... any n+1 points which do not lie in an (n-1)-space are the vertices of an n-dimensional simplex.... Thus the general simplex may alternatively be defined as a finite region of n-space enclosed by n+1 hyperplanes or (n-1)-spaces."
- ↑ van Ittersum 2020, p. 78, §4.2.5.
- ↑ Stillwell 2001, p. 18-21.
- ↑ Egan 2021; quaternions, the binary tetrahedral group and the binary octahedral group, with rotating illustrations.
- ↑ Stillwell 2001, p. 22.
- ↑ Coxeter 1973, p. 163: Coxeter notes that Thorold Gosset was apparently the first to see that the cells of the 24-cell honeycomb {3,4,3,3} are concentric with alternate cells of the tesseractic honeycomb {4,3,3,4}, and that this observation enabled Gosset's method of construction of the complete set of regular polytopes and honeycombs.
- ↑ Jump up to: 40.0 40.1 Coxeter 1973, p. 156: "...the chess-board has an n-dimensional analogue."
- ↑ Mamone, Pileio & Levitt 2010, pp. 1438-1439, §4.5 Regular Convex 4-Polytopes; the 24-cell has 1152 symmetry operations (rotations and reflections) as enumerated in Table 2, symmetry group 𝐹4.
- ↑ Coxeter 1973, p. 119, §7.1. Dimensional Analogy: "For instance, seeing that the circumference of a circle is 2π r, while the surface of a sphere is 4π r 2, ... it is unlikely that the use of analogy, unaided by computation, would ever lead us to the correct expression [for the hyper-surface of a hyper-sphere], 2π 2r 3."
- ↑ Kim & Rote 2016, p. 6, §5. Four-Dimensional Rotations.
- ↑ Perez-Gracia & Thomas 2017, §7. Conclusions; "Rotations in three dimensions are determined by a rotation axis and the rotation angle about it, where the rotation axis is perpendicular to the plane in which points are being rotated. The situation in four dimensions is more complicated. In this case, rotations are determined by two orthogonal planes and two angles, one for each plane. Cayley proved that a general 4D rotation can always be decomposed into two 4D rotations, each of them being determined by two equal rotation angles up to a sign change."
- ↑ Perez-Gracia & Thomas 2017.
- ↑ Perez-Gracia & Thomas 2017, pp. 12−13, §5. A useful mapping.
- ↑ Coxeter 1995, pp. 30-32, (Paper 3) Two aspects of the regular 24-cell in four dimensions; §3. The Dodecagonal Aspect;[lower-alpha 86] Coxeter considers the 150°/30° double rotation of period 12 which locates 12 of the 225 distinct 24-cells inscribed in the 120-cell, a regular 4-polytope with 120 dodecahedral cells that is the convex hull of the compound of 25 disjoint 24-cells.
- ↑ Perez-Gracia & Thomas 2017, pp. 2−3, §2. Isoclinic rotations.
- ↑ Kim & Rote 2016, pp. 7-10, §6. Angles between two Planes in 4-Space.
- ↑ Coxeter 1973, p. 141, §7.x. Historical remarks; "Möbius realized, as early as 1827, that a four-dimensional rotation would be required to bring two enantiomorphous solids into coincidence. This idea was neatly deployed by H. G. Wells in The Plattner Story."
- ↑ Feynman & Weinberg 1987, The reason for antiparticles.
- ↑ Mebius 2015, pp. 2-3, Motivation; "This reseach originated from ... the desire to construct a computer implementation of a specific motion of the human arm, known among folk dance experts as the Philippine wine dance or Binasuan and performed by the late physicist Richard P. Feynman during his Dirac memorial lecture 1986[51] to show that a single rotation (2𝝅) is not equivalent in all respects to no rotation at all, whereas a double rotation (4𝝅) is."
- ↑ Dorst 2019, p. 44, §1. Villarceau Circles; "In mathematics, the path that the (1, 1) knot on the torus traces is also known as a Villarceau circle. Villarceau circles are usually introduced as two intersecting circles that are the cross-section of a torus by a well-chosen plane cutting it. Picking one such circle and rotating it around the torus axis, the resulting family of circles can be used to rule the torus. By nesting tori smartly, the collection of all such circles then form a Hopf fibration.... we prefer to consider the Villarceau circle as the (1, 1) torus knot rather than as a planar cut."
- ↑ Kim & Rote 2016, pp. 8-9, Relations to Clifford parallelism.
- ↑ Kim & Rote 2016, p. 8, Left and Right Pairs of Isoclinic Planes.
- ↑ Tyrrell & Semple 1971, pp. 1-9, §1. Introduction.
- ↑ Tyrrell & Semple 1971, pp. 20-33, Clifford Parallel Spaces and Clifford Reguli.
- ↑ Coxeter 1973, pp. 292-293, Table I(i): Octahedron.
- ↑ Kim & Rote 2016, pp. 14-16, §8.3 Properties of the Hopf Fibration; Corollary 9. Every great circle belongs to a unique right [(and left)] Hopf bundle.
- ↑ Kim & Rote 2016, p. 12, §8 The Construction of Hopf Fibrations; 3.
- ↑ Tyrrell & Semple 1971, pp. 34-57, Linear Systems of Clifford Parallels.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); 24-cell h1 is {12}, h2 is {12/5}.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); 24-cell Petrie polygon h1 is {12}.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); 24-cell Petrie polygon orthogonal h2 is {12/5}, half of {24/5} as each Petrie polygon is half the 24-cell.
- ↑ Coxeter 1973, pp. 292-293, Table I(ii); "24-cell".
- ↑ Coxeter 1973, p. 139, §7.9 The characteristic simplex.
- ↑ Coxeter 1973, p. 290, Table I(ii); "dihedral angles".
- ↑ Coxeter 1973, pp. 130-133, §7.6 The symmetry group of the general regular polytope.
- ↑ Kim & Rote 2016, pp. 17-20, §10 The Coxeter Classification of Four-Dimensional Point Groups.
- ↑ Coxeter 1973, pp. 33-38, §3.1 Congruent transformations.
- ↑ Coxeter 1973, pp. 217-218, §12.2 Congruent transformations.
- ↑ Coxeter 1973, p. 138; "We allow the Schläfli symbol {p,..., v} to have three different meanings: a Euclidean polytope, a spherical polytope, and a spherical honeycomb. This need not cause any confusion, so long as the situation is frankly recognized. The differences are clearly seen in the concept of dihedral angle."
- ↑ Mamone, Pileio & Levitt 2010, pp. 1438-1439, §4.5 Regular Convex 4-Polytopes, Table 2, Symmetry operations.
- ↑ Coxeter 1970, p. 18, §8. The simplex, cube, cross-polytope and 24-cell; Coxeter studied cell rings in the general case of their geometry and group theory, identifying each cell ring as a polytope in its own right which fills a three-dimensional manifold (such as the 3-sphere) with its corresponding honeycomb. He found that cell rings follow Petrie polygons[lower-alpha 86] and some (but not all) cell rings and their honeycombs are twisted, occurring in left- and right-handed chiral forms. Specifically, he found that since the 24-cell's octahedral cells have opposing faces, the cell rings in the 24-cell are of the non-chiral (directly congruent) kind.[lower-alpha 118] Each of the 24-cell's cell rings has its corresponding honeycomb in Euclidean (rather than hyperbolic) space, so the 24-cell tiles 4-dimensional Euclidean space by translation to form the 24-cell honeycomb.
- ↑ Banchoff 2013, studied the decomposition of regular 4-polytopes into honeycombs of tori tiling the Clifford torus, showed how the honeycombs correspond to Hopf fibrations, and made a particular study of the 24-cell's 4 rings of 6 octahedral cells with illustrations.
- ↑ Banchoff 2013, pp. 265-266.
- ↑ Coxeter 1991.
References
- Kepler, Johannes (1619). Harmonices Mundi (The Harmony of the World). Johann Planck.
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
- Coxeter, H.S.M. (1991), Regular Complex Polytopes (2nd ed.), Cambridge: Cambridge University Press
- Coxeter, H.S.M. (1995), Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C. et al., eds., Kaleidoscopes: Selected Writings of H.S.M. Coxeter (2nd ed.), Wiley-Interscience Publication, ISBN 978-0-471-01003-6, https://archive.org/details/kaleidoscopessel0000coxe
- (Paper 3) H.S.M. Coxeter, Two aspects of the regular 24-cell in four dimensions
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, H.S.M. (1968). The Beauty of Geometry: Twelve Essays (2nd ed.). New York: Dover.
- Coxeter, H.S.M. (1989). "Trisecting an Orthoscheme". Computers Math. Applic. 17 (1–3): 59–71. doi:10.1016/0898-1221(89)90148-X.
- Coxeter, H.S.M. (1970), "Twisted Honeycombs", Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics (Providence, Rhode Island: American Mathematical Society) 4
- Stillwell, John (January 2001). "The Story of the 120-Cell". Notices of the AMS 48 (1): 17–25. https://www.ams.org/notices/200101/fea-stillwell.pdf.
- Johnson, Norman (2018), Geometries and Transformations, Cambridge: Cambridge University Press, ISBN 978-1-107-10340-5, https://www.cambridge.org/core/books/geometries-and-transformations/94D1016D7AC64037B39440729CE815AB
- Johnson, Norman (1991), Uniform Polytopes (Manuscript ed.)
- Johnson, Norman (1966), The Theory of Uniform Polytopes and Honeycombs (Ph.D. ed.)
- Weisstein, Eric W.. "24-Cell". http://mathworld.wolfram.com/24-Cell.html. (also under Icositetrachoron)
- Klitzing, Richard. "4D uniform polytopes (polychora) x3o4o3o - ico". https://bendwavy.org/klitzing/dimensions/polychora.htm.
- Ghyka, Matila (1977). The Geometry of Art and Life. New York: Dover Publications. ISBN 978-0-486-23542-4.
- Banchoff, Thomas F. (2013). "Torus Decompostions of Regular Polytopes in 4-space". in Senechal, Marjorie. Shaping Space. Springer New York. pp. 257–266. doi:10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8. https://archive.org/details/shapingspaceexpl00sene.
- Copher, Jessica (2019). "Sums and Products of Regular Polytopes' Squared Chord Lengths". arXiv:1903.06971 [math.MG].
- van Ittersum, Clara (2020). Symmetry groups of regular polytopes in three and four dimensions (Thesis). Delft University of Technology.
- Kim, Heuna; Rote, G. (2016). "Congruence Testing of Point Sets in 4 Dimensions". arXiv:1603.07269 [cs.CG].
- Perez-Gracia, Alba; Thomas, Federico (2017). "On Cayley's Factorization of 4D Rotations and Applications". Adv. Appl. Clifford Algebras 27: 523–538. doi:10.1007/s00006-016-0683-9. https://upcommons.upc.edu/bitstream/handle/2117/113067/1749-ON-CAYLEYS-FACTORIZATION-OF-4D-ROTATIONS-AND-APPLICATIONS.pdf.
- Waegell, Mordecai; Aravind, P. K. (2009-11-12). "Critical noncolorings of the 600-cell proving the Bell-Kochen-Specker theorem" (in en). Journal of Physics A: Mathematical and Theoretical 43 (10): 105304. doi:10.1088/1751-8113/43/10/105304.
- Tyrrell, J. A.; Semple, J.G. (1971). Generalized Clifford parallelism. Cambridge University Press. ISBN 0-521-08042-8. https://archive.org/details/generalizedcliff0000tyrr.
- Egan, Greg (23 December 2021). "Symmetries and the 24-cell". https://www.gregegan.net/SCIENCE/24-cell/24-cell.html.
- Mamone, Salvatore; Pileio, Giuseppe; Levitt, Malcolm H. (2010). "Orientational Sampling Schemes Based on Four Dimensional Polytopes". Symmetry 2 (3): 1423–1449. doi:10.3390/sym2031423. Bibcode: 2010Symm....2.1423M.
- Mebius, Johan (July 2015) [11 Jan 1994]. Applications of Quaternions to Dynamical Simulation, Computer Graphics and Biomechanics (Thesis). Delft University of Technology. doi:10.13140/RG.2.1.3310.3205.
- Feynman, Richard; Weinberg, Steven (1987). Elementary particles and the laws of physics. Cambridge University Press.
- Dorst, Leo (2019). "Conformal Villarceau Rotors". Advances in Applied Clifford Algebras 29 (44). doi:10.1007/s00006-019-0960-5.
External links
- 24-cell animations
- 24-cell in stereographic projections
- 24-cell description and diagrams
- Petrie dodecagons in the 24-cell: mathematics and animation software
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |