Physics:Coulomb's constant

Coulomb's constant, the electric force constant, or the electrostatic constant (denoted k_e, k or K) is a proportionality constant in electrodynamics equations. In SI units, it is exactly equal to 8987551787.3681764 N·m²·C⁻², or roughly equaling 8.99×10⁹ N·m²·C⁻². It was named after the French physicist Charles-Augustin de Coulomb (1736–1806) who introduced Coulomb's law.

Value of the constant

Coulomb's constant is the constant of proportionality in Coulomb's law,

[math]\displaystyle{ \mathbf{F} = k_\text{e}\frac{Qq}{r^2}\mathbf{\hat{e}}_r }[/math]

where ê_r is a unit vector in the r-direction and

[math]\displaystyle{ k_\text{e} = \alpha \frac{\hbar c}{e^2} }[/math],

where α is the fine-structure constant, c is the speed of light, ħ is the reduced Planck constant, and e is elementary charge. In SI:

[math]\displaystyle{ k_\text{e} = \frac{1}{4\pi\varepsilon_0} }[/math],

where [math]\displaystyle{ \varepsilon_0 }[/math] is the vacuum permittivity. This formula can be derived from Gauss' law,

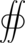[math]\displaystyle{ {\scriptstyle S} }[/math] [math]\displaystyle{ \mathbf{E} \cdot {\rm d}\mathbf{A} = \frac{Q}{\varepsilon_0} }[/math]

Taking this integral for a sphere, radius r, around a point charge, we note that the electric field points radially outwards at all times and is normal to a differential surface element on the sphere, and is constant for all points equidistant from the point charge.

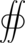[math]\displaystyle{ {\scriptstyle S} }[/math] [math]\displaystyle{ \mathbf{E} \cdot {\rm d}\mathbf{A} = |\mathbf{E}|\mathbf{\hat{e}}_r\int_{S} dA = |\mathbf{E}|\mathbf{\hat{e}}_r \times 4\pi r^{2} }[/math]

Noting that E = F/Q for some test charge q,

[math]\displaystyle{ \begin{align} \mathbf{F} &= \frac{1}{4\pi\varepsilon_0}\frac{Qq}{r^2}\mathbf{\hat{e}}_r = k_\text{e}\frac{Qq}{r^2}\mathbf{\hat{e}}_r \\[8pt] \therefore k_\text{e} &= \frac{1}{4\pi\varepsilon_0} \end{align} }[/math]

In modern systems of units Coulomb's constant k_e is an exact constant, in Gaussian units k_e = 1, in Lorentz–Heaviside units (also called rationalized) k_e = 1/4π and in SI k_e = 1/4πε₀, where the vacuum permittivity ε₀ = 1/μ₀c² ≈ 8.85418782×10⁻¹² F m⁻¹, the speed of light in vacuum c is 299792458 m/s, the vacuum permeability μ₀ is 4π×10⁻⁷ H m⁻¹, so that

[math]\displaystyle{ \begin{align} k_\text{e} = \frac{1}{4\pi\varepsilon_0}=\frac{c^2\mu_0}{4\pi}&=c^2\times (10^{-7}\ \mathrm{H\ m}^{-1})\\ &= 8.987\,551\,787\,368\,1764\times 10^9~\mathrm{N\ m^2\ C^{-2}}. \end{align} }[/math]

Use of Coulomb's constant

Coulomb's constant is used in many electric equations, although it is sometimes expressed as the following product of the vacuum permittivity constant:

[math]\displaystyle{ k_\text{e} = \frac{1}{4\pi\varepsilon_0}. }[/math]

Coulomb's constant appears in many expressions including the following:

Coulomb's law:

[math]\displaystyle{ \mathbf{F}=k_\text{e}{Qq\over r^2}\mathbf{\hat{e}}_r. }[/math]

Electric potential energy:

[math]\displaystyle{ U_\text{E}(r) = k_\text{e}\frac{Qq}{r}. }[/math]

Electric field:

[math]\displaystyle{ \mathbf{E} = k_\text{e} \sum_{i=1}^N \frac{Q_i}{r_i^2} \mathbf{\hat{r}}_i. }[/math]

See also

• Gravitational constant
• Vacuum permittivity
• Vacuum permeability