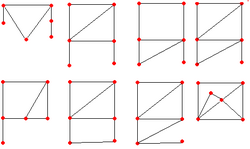
Asymmetric graph
In graph theory, a branch of mathematics, an undirected graph is called an asymmetric graph if it has no nontrivial symmetries.
Formally, an automorphism of a graph is a permutation p of its vertices with the property that any two vertices u and v are adjacent if and only if p(u) and p(v) are adjacent. The identity mapping of a graph onto itself is always an automorphism, and is called the trivial automorphism of the graph. An asymmetric graph is a graph for which there are no other automorphisms.
Note that the term "asymmetric graph" is not a negation of the term "symmetric graph," as the latter refers to a stronger condition than possessing nontrivial symmetries.
Examples
The smallest asymmetric non-trivial graphs have 6 vertices.[1] The smallest asymmetric regular graphs have ten vertices; there exist ten-vertex asymmetric graphs that are 4-regular and 5-regular.[2]Cite error: Closing </ref> missing for <ref> tag
Trees
The smallest asymmetric tree has seven vertices: it consists of three paths of lengths 1, 2, and 3, linked at a common endpoint.[3] In contrast to the situation for graphs, almost all trees are symmetric. In particular, if a tree is chosen uniformly at random among all trees on n labeled nodes, then with probability tending to 1 as n increases, the tree will contain some two leaves adjacent to the same node and will have symmetries exchanging these two leaves.[1]
References
- ↑ 1.0 1.1 Cite error: Invalid
<ref>tag; no text was provided for refs nameder63 - ↑ Baron, G.; Imrich, W. (1969), "Asymmetrische reguläre Graphen", Acta Mathematica Academiae Scientiarum Hungaricae 20: 135–142, doi:10.1007/BF01894574.
- ↑ Quintas, Louis V. (1967), "Extrema concerning asymmetric graphs", Journal of Combinatorial Theory 3 (1): 57–82, doi:10.1016/S0021-9800(67)80018-8.
 |